運輸經濟學/生產

生產

介紹

運輸利用各種車輛在不同的基礎設施系統上將人員和貨物從一個地方移動到另一個地方。它不僅使用技術（即車輛、能源和基礎設施），還使用人們的時間和努力；不僅產生乘客出行和貨物運輸的預期產出，還產生諸如空氣汙染、噪音、擁堵、碰撞、傷害和死亡等不利結果。

圖 1 說明了運輸的投入、產出和結果。在左上角是傳統的投入（基礎設施（包括路面、橋樑等）、生產運輸所需的勞動力、基礎設施佔用的土地、能源投入和車輛）。基礎設施是傳統土木工程的保留地，而車輛則紮根於機械工程。能源，就其為現有車輛提供動力而言，是一個機械工程問題，但旨在減少或最大限度地減少能源消耗的系統設計需要超越傳統的學科界限思考。

在圖的頂部是資訊、運營和管理以及旅行者的時間和精力。運輸系統為人們服務，並由人們建立，包括系統所有者和運營商，他們運營、管理和維護系統，以及使用系統的旅行者。旅行者的時間取決於自由流時間，它是基礎設施設計的結果，以及由於擁堵造成的延誤，這是系統容量及其使用量的相互作用。在圖的右上角是運輸的不利結果，尤其是其負外部性

透過汙染，系統消耗健康並增加發病率和死亡率；
因為危險，它們消耗安全並造成傷害和死亡；
因為嘈雜，它們消耗安靜併產生噪音（降低生活質量和財產價值）；以及
透過排放碳和其他汙染物，它們損害環境。

所有這些因素都越來越被認為是運輸的成本，但最值得注意的是環境影響，尤其是對全球氣候變化的擔憂。圖的底部顯示了運輸的產出。運輸是經濟活動和人們生活的核心，它使他們能夠從事工作、上學、購買食物和其他商品，並參與構成人類存在的所有活動。更多的運輸，透過增加對更多目的地的可達性，使人們能夠更好地滿足他們的個人目標，但也意味著更高的個人和社會成本。雖然“運輸問題”通常以擁堵的方式提出，但這種延誤只是擁有許多成本和更多益處的系統的成本之一。此外，透過改變可達性，運輸塑造了土地的開發。

運輸與生產

運輸是一個生產過程，也是企業、城市、州和國家生產函式中的一個要素投入。運輸是由各種服務產生的，並與其他投入一起用於生產經濟中的商品和服務。運輸是一種中間產品，因此它具有“派生需求”。生產理論可以指導我們思考如何有效地生產運輸以及如何有效地利用運輸來生產其他商品。

更廣泛地說，人們將運輸作為投入進入生產過程。例如，國民生產總值（GNP）是衡量產出的指標，它是用資本、勞動力、能源、材料和運輸作為投入生產的。GNP = f(K, L, E, M, T)

或者，我們可以將運輸視為產出：例如，航空服務的客運里程、貨運服務的噸公里或公共汽車的執行里程。這些產出是由包括運輸在內的投入產生的。

T = g(K, L, E, M,)

本章將重點介紹後一種觀點。

生產過程涉及大量的投入和產出。通常需要對這些投入和產出進行彙總，以便分析更易於管理；例如包括各種型別勞動和各種型別運輸。

衡量投入和產出

物質投入 - 體積/質量
人力投入 - 勞動力和使用者（時間）
服務投入 - 導航、碼頭運營
資本投入 - 物理單位、貨幣單位（存量和流量）
設計投入 - 尺寸、重量、功率
運輸 - 貨運航程、車輛航程、車輛里程、容量里程、里程

運輸生產的特徵

在運輸中，產出是“服務”，而不是產品。它不可儲存（現在未使用的容量不能以後出售，這導致了高峰/非高峰的經濟學），使用者參與生產（乘客是生產產出的關鍵因素）。

投入由承運人、使用者和公眾提供

承運人：碼頭活動、幹線活動等。
使用者：時間價值等。
公眾：基礎設施

生產的特點是多維（異構）產出。

數量：最常見的產出衡量指標；
- 噸公里
- 客運公里
空間維度 - 起點-終點和方向
時間維度 - 運輸時間、高峰和季節性
服務質量 - 速度、可靠性等。

以下表格說明了在考慮投入和產出時使用生產方法進行系統設計的示例

投入	產出
維度	表面積/體積承載能力
尺寸、速度	運輸能力（例如，每小時車輛數）
系統容量、基礎設施質量	交通流量
容量、車輛移動	O-D 航程
跑道、航站樓	乘客和飛機的移動

大塊投資是指投資的不可分割性導致複雜的成本核算和定價。例如，您不能建造半條車道或半條跑道，然後使其變得有用。

沉沒投資可能構成進入壁壘。

聯合生產是指不可避免地以固定比例生產多種產出，例如，正向運輸-反向運輸問題；存在聯合成本分配問題。聯合成本是指多種產品以固定不變的比例存在。

在共同生產中，使用相同裝置或設施生產比例不同的多種產出 - 節省成本的優勢，例如，貨運和客運服務使用同一架飛機，或使用同一列火車。共同成本是指多種服務可以以可變比例生產，而成本支出相同

承運人有一個結構，可以分解為兩個主要活動（碼頭和幹線）

碼頭活動包括貨物的裝卸和分揀（以及可能包括提貨和送貨）。速度的概念對於碼頭來說可能很重要，而要行駛的距離則與之關係不大。碼頭活動可能因貨物型別而異，例如，我們看到散裝裝卸設施的規模收益遞增，但對於處理各種產品型別的設施而言，規模收益遞增是否明顯尚不清楚。

幹線活動表現出由於以下原因導致供給方產出單位的不可分割性

容量塊和產出不可儲存性（需求和生產數量之間的不匹配）
反向運輸能力的聯合生產
共同生產；例如，短途市場與長途市場一起服務。

生產理論

生產理論分析了企業如何在給定技術的情況下，將投入（ $x$ ）轉化為產出（ $y$ ），以經濟有效的方式。生產函式， $y=f(x)$ ，用於描述產出與投入之間的關係。

效率

X效率是指使用給定投入組合生產產出的效率。如果企業在僱傭資源的情況下能夠生產出最大產出，那麼它就是X效率的。

配置效率是指資源配置以最大限度地實現資源使用帶來的淨收益的市場狀態。在這種市場狀態下，不可能讓一個人變得更好，而不會讓另一個人變得更糟。

技術效率是指用最少的投入生產給定產出的能力，或者等效地，在生產邊界上執行而不是在其內部執行。

生產可能性集

生產可能性集是投入和產出可行組合的集合。例如，為了生產一定數量的客運量，飛機可以經常加油，從而減少油量，或者減少加油次數，並增加油量。產出是車輛行駛量，投入是燃油和勞動力。

如果生產可能性集 (PPS) 是凸的，那麼可以根據單個條件識別出最佳投入組合。但是，如果 PPS 不是凸的，那麼標準就會變得模稜兩可。我們需要檢視整個等產量曲線才能找到最佳值，但在沒有凸性的情況下，我們會變得“近視”，如右側所示。

投入價格的線性齊次性

$C\left(Q,2P_{1},2P_{2}\right)=2C\left(Q,P_{1},P_{2}\right)$

所有產出的邊際成本都為正

${\frac {\partial C}{\partial Q_{j}}}>0\forall j$ .

成本函式對投入價格的導數產生投入需求函式。

${\frac {\partial C}{\partial P_{j}}}=X\left(\bullet \right)$

隨著投入價格的上升，我們總是會從相對更昂貴的投入中進行替代。

${\frac {\partial ^{2}C}{\partial P_{i}^{2}}}\leq 0\forall i$

函式形式

生產函式是在給定技術的情況下，投入和產出之間的關係。技術的變化可以影響生產函式，主要體現在兩個方面。首先，它會改變產出水平，因為它會影響所有投入，其次，它會透過改變投入組合來提高產出。大多數生產函式是在技術保持不變的假設下估計的。這類似於在估計需求關係時假設消費者偏好保持不變或不變。

函式形式表示投入的組合方式。這些形式可以從簡單的線性或對數線性（柯布-道格拉斯）關係到以“對數函式”表示的二階近似。

線性

線性生產函式是最簡單的

Y=A+\alpha L+\beta K

二次方程

二次生產函式增加了平方項和互動項。

Y=A+\alpha L+\beta K+\gamma L^{2}+\phi K^{2}+\rho KL

柯布-道格拉斯

(改編自維基百科關於柯佈道格拉斯函式的文章 )

對於生產，柯布-道格拉斯函式是

Y=AL^{\alpha }K^{\beta },

其中

Y = 總產量（一年內生產的所有商品的貨幣價值）
L = 勞動力投入
K = 資本投入
A = 全要素生產率
$\alpha$ 和 $\beta$ 分別是產出彈性，分別代表勞動力和資本。這些值是由可用技術決定的常數。

產出彈性衡量的是產出對生產中使用勞動力或資本水平變化的響應程度，在其他條件不變的情況下。例如，如果 $\alpha =0.15$ ，勞動力增長 1% 將導致產出大約增長 0.15%。

此外，如果

\alpha +\beta =1

生產函式具有規模報酬不變。也就是說，如果 L 和 K 都增加 20%，Y 將增加 20%。如果

\alpha +\beta <1

規模報酬遞減，如果

\alpha +\beta >1

規模報酬遞增。假設完全競爭和 $\alpha +\beta =1$ ， $\alpha$ 和 $\beta$ 可以證明是勞動力和資本在產出中的份額。

Translog

Translog 生產函式是柯布-道格拉斯生產函式的推廣。Translog 代表“超越對數”。

雙要素 Translog 生產函式是

{\begin{aligned}\ln(Y)&=\ln(A)+a_{L}\ln(L)+a_{K}\ln(K)+b_{LL}\ln(L)\ln(L)\\&{}\qquad {}+b_{KK}\ln(K)\ln(K)+b_{LK}\ln(L)\ln(K)\\&=f(L,K).\end{aligned}}

其中 L = 勞動力，K = 資本，Y = 產品。

CES（替代彈性恆定）

替代彈性恆定（CES）函式： $Y=A[\alpha K^{\gamma }+(1-\alpha )L^{\gamma }]^{\frac {1}{\gamma }}$

$\gamma =0$ 對應於科布-道格拉斯函式， $Y=AK^{\alpha }L^{1-\alpha }$

列昂惕夫

該列昂惕夫生產函式適用於投入必須以固定比例使用的場合；從這些比例開始，如果增加一種投入的使用量而另一種投入的使用量沒有增加，產出將不會發生變化。該生產函式由以下公式給出：

Y=\min(aK,\ \ bL,\ \ ...).

生產函式的特徵

生產關係的考察需要理解生產函式的性質。考慮將產出與兩個投入聯絡起來的一般生產函式（這裡只用兩個投入是為了說明方便，結論在考慮更多投入或產出時不會改變，只是更復雜而已）

$Q=f(K,L)$

考慮將資本量固定在某個水平上，並考察在增加勞動力（可變要素）投入量時產出的變化。我們對 $\Delta Q/\Delta L$ 感興趣，它被定義為勞動力的邊際產量，以及 $Q/L$ 勞動的平均產量。對於任何投入，都可以定義這些，勞動只是用作示例。

這表示一個“普通”的生產函式。這描述了一個短期關係。它是短期，因為至少一個投入是固定的。考察在一種投入變化時產出的行為是有指導意義的。

請注意，平均產量 (AP) 上升並達到最大值，在該點，射線的斜率 $Q/L$ 達到最大值，然後漸近遞減。

邊際產量 (MP) 上升（邊際生產率上升區域），在 AP 上方，並達到最大值。它下降（邊際生產率下降區域），並在 AP 的最大值處與 AP 相交。當總產量 (TP) 達到最大值時，MP 降至零。應該清楚為什麼使用 AP 作為生產力指標（政府、行業、工程師等經常使用的指標）是非常可疑的。例如，在 $MP=0$ 之後， $AP>0$ ，但 TP 正在下降。

這裡的“邊際生產率遞減原理”得到了很好的體現。該原理指出，當你在固定要素中新增可變要素的單位時，最初產量將上升，而且很可能以越來越快的速度上升（但不一定），但在某個時刻，新增更多可變投入將對總產出的貢獻越來越少，最終可能導致總產出下降（同樣不一定）。

固定要素（或技術）的任何變化都會導致 TP、AP 和 MP 函式向上移動。這提出了一個有趣且重要的議題，即是什麼產生了產出的變化；可變要素的變化、技術的變化，或者技術的變化。

等產量曲線

等產量曲線揭示了關於技術和替代性的很多資訊。與無差異曲線類似，等產量曲線的曲率表示兩種要素之間的替代程度。它們越“直角化”，替代程度越低。此外，邊際產量遞減在等產量曲線的斜率中起作用，因為隨著要素比例的變化，相對邊際產量的變化。因此，替代性不僅僅是生產技術的問題，也是投入的相對比例的問題。

與其考慮一個可變要素，不如考慮兩個（或所有）可變要素。

$Q=f(K,L)$ .

取全微分並令其等於零

$dQ={\frac {\partial f}{\partial K}}dK+{\frac {\partial f}{\partial L}}dL=0$

重新排列可以看出，邊際生產率之比 ( ${\frac {MP_{K}}{MP_{L}}}$ ) 等於 ${\frac {dk}{dL}}$

等價地，等產量曲線是K 和 L 組合的軌跡，這些組合將產生相同的產量水平，並且等產量曲線的斜率（ ${\frac {dk}{dL}}$ ）等於邊際產量之比。

邊際產出之比也稱為“技術替代邊際率”MRTS。

當從原點向外移動時，產量水平會上升，但與無差異曲線不同，等產量曲線是可以進行基數度量的。它們之間的距離將反映生產技術的特徵。

等產量曲線模型可以用來說明尋找以最低成本生產給定產量的解決方案，或者等價地，從給定預算中獲得最大產量的解決方案。最裡面的預算線對應於與預算線相交的投入價格，最佳數量是最佳成本與預算線交點處的座標。該解決方案可以是內部解決方案或角點解決方案，如下面的圖表所示。

約束最佳化

這個剛剛說明的約束最佳化問題的例子是

${\begin{aligned}&{\text{Min cost }}={\text{ }}p_{1}x_{1}+p_{2}x_{2}\\&{\text{s}}{\text{.t}}{\text{. }}F(x_{1},x_{2})=Q\\\end{aligned}}$

其中

f() 是生產函式
目標函式（最小成本）：願望
約束（受制於）：必要性
$x_{1},x_{2}$ : 決策變數

拉格朗日乘子法是一種透過引入額外的決策變數將約束問題轉化為無約束問題的方法。這些“新的”決策變數具有有趣的經濟解釋。

${\begin{aligned}&{\text{Max }}g\left({\bar {x}}\right)\\&{\text{s}}{\text{.t}}{\text{. }}h_{j}\left({\bar {x}}\right)=b_{j}\\\end{aligned}}$

拉格朗日函式

${\text{Max}}\Lambda \left({\bar {x}},{\bar {\lambda }}\right)=g\left({\bar {x}}\right)-\sum {{\bar {\lambda }}_{j}\left(h_{j}\left({\bar {x}}\right)-b_{j}\right)}$

為了找到最大值，取一階導數並將其設定為零

${\frac {\partial \Lambda }{\partial x_{i}}}={\frac {\partial g}{\partial x_{i}}}-\sum \limits _{j}{\lambda _{j}}{\frac {\partial h_{j}}{\partial x_{i}}}=0$

${\frac {\partial \Lambda }{\partial \lambda _{j}}}=-h_{j}\left(x\right)+b_{j}=0$

拉格朗日函式被最大化（最小化）
拉格朗日函式等於原始目標函式
約束條件得到滿足

拉格朗日乘子代表如果約束條件發生變化，目標函式將發生變化的幅度。因此，例如，當與生產函式一起使用時，拉格朗日函式將被解釋為預算約束的“影子價格”，即如果預算增加一個單位，產量可以增加的幅度，或者等價地，增加一個單位產量的邊際成本。

示例

${\begin{aligned}&{\text{Min cost }}={\text{ }}p_{1}x_{1}+p_{2}x_{2}\\&{\text{s}}{\text{.t}}{\text{. }}F(x_{1},x_{2})=Q\\\end{aligned}}$

$\Lambda =p_{1}x_{1}+p_{2}x_{2}-\lambda (F(x_{1},x_{2})-Q)$

${\frac {\partial \Lambda }{\partial x_{1}}}=-p_{\text{1}}-\lambda {\frac {\partial F\left(x_{\text{1}},x_{\text{2}}\right)}{\partial x_{\text{1}}}}=0$

${\frac {\partial \Lambda }{\partial x_{2}}}=-p_{\text{2}}-\lambda {\frac {\partial F\left(x_{\text{1}},x_{\text{2}}\right)}{\partial x_{\text{2}}}}=0$

${\frac {\partial \Lambda }{\partial \lambda _{j}}}=Q-F\left(x_{\text{1}},x_{\text{2}}\right)=0$

${\frac {p_{\text{1}}}{\frac {\partial F\left(x_{\text{1}},x_{\text{2}}\right)}{\partial x_{\text{1}}}}}=\lambda$

${\frac {p_{2}}{\frac {\partial F\left(x_{\text{1}},x_{\text{2}}\right)}{\partial x_{2}}}}=\lambda$

${\frac {p_{\text{1}}}{p_{2}}}={\frac {\frac {\partial F\left(x_{\text{1}},x_{\text{2}}\right)}{\partial x_{\text{1}}}}{\frac {\partial F\left(x_{\text{1}},x_{\text{2}}\right)}{\partial x_{2}}}}$

所以

$\lambda ={\frac {\partial \Lambda }{\partial Q}}$

等於邊際產出成本。

條件

一階條件（FOC）不足以定義最小值或最大值。

二階條件也是必需的。然而，如果生產集是凸的，並且投入成本函式是線性的，那麼FOC足以定義最大產出或最小成本。

最佳化

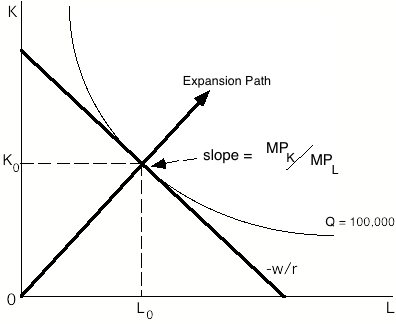
利潤最大化的公司將僱用要素，直到這些要素對收入的貢獻等於對成本的貢獻為止。等產量曲線有助於說明這一點。

考慮一家利潤最大化的公司，以及它選擇最優要素組合的決定。

$\Pi =Pf\left(K,L\right)-\left(wL+rK\right)$

${\frac {\partial \Pi }{\partial K}}=P{\frac {\partial f}{\partial K}}-r=0$

${\frac {\partial \Pi }{\partial L}}=P{\frac {\partial f}{\partial L}}-w=0$

這表明，利潤最大化的公司將僱用生產要素，直到它們對收入的貢獻（邊際收益產品）或產品價格乘以生產要素的邊際產量等於它們對公司的成本貢獻。這個解決方案可以透過等產量圖來說明。

均衡點，即最佳投入組合，是指公司可以將一種投入與另一種投入之間進行交易的比率（由技術決定的），正好等於市場允許您將一種生產要素與另一種生產要素之間進行交易的比率（由相對工資率決定的）。這個均衡點應該被認為等同於成本函式上的一個點。請注意，這在原則上與需求中的效用空間和產出空間相同。它還指出了一個可能影響成本的重要因素；即您是否處於擴張路徑上。

為了從生產函式轉換到成本函式，我們需要找到投入成本最小化的投入組合來生產給定的產出。我們已經看到，這就是擴張路徑。因此，從生產函式到成本函式的轉換需要三個關係

生產函式
預算約束
擴張路徑

“生產成本函式”是指生產給定產出可能的最低成本。

對偶性

生產函式和成本函式之間存在著對偶關係。這意味著生產函式中包含的所有資訊也包含在成本函式中，反之亦然。因此，正如從消費者支出資訊中可以恢復偏好對映一樣，也可以從成本函式中恢復生產函式。

假設我們知道成本函式 C(Q,P')，其中 P" 是投入價格向量。如果我們讓產出和投入價格取值 C˚, P˚1 和 P˚2，我們可以推匯出生產函式。

1. 瞭解產出水平和投入價格的具體值意味著我們知道最佳投入組合，因為等產量曲線的斜率等於相對價格的比率。

2. 瞭解等產量曲線的斜率意味著我們知道預算線的斜率

3. 我們知道產出水平。

因此，我們可以針對我們想要的任何 Q 和 P 值生成類似的陳述，因此可以繪製完整的等產量圖，除了不是最佳投入組合的投入組合。

要素需求函式

從生產分析中得出的一個重要概念是，對生產要素的需求是派生需求；也就是說，人們不需要它本身，而是為了它能生產的東西。對生產要素的需求函式是從其邊際產量曲線得出的，事實上，要素需求曲線是邊際產量曲線中位於平均產量曲線以下的部分。隨著要素使用量的增加，邊際產量將下降，因此沿著要素需求曲線下降。如果生產要素用於生產的產品的價格發生變化，要素需求函式將發生移動。同樣，技術進步將導致邊際產量曲線發生移動。

投入成本函式

回想一下，我們的生產函式 Q = f(x1, x2) 可以轉換為成本函式，因此我們從投入空間轉移到美元空間。生產函式是一個技術關係，而成本函式不僅包括技術，還包括最佳化行為。

轉換需要一個預算約束或投入價格。將存在可行的非最佳投入組合，這些組合可以產生給定的產出，以及可行的最佳投入組合，這些組合可以產生最佳解決方案。

技術變革

技術變革可以以三種基本形式進入生產函式；長期、創新和設施或基礎設施。

技術變革可以影響生產函式中的所有生產要素，從而成為“要素中性”，或者它可能對生產要素的影響不同，在這種情況下它將是“要素偏向”。

技術變革的結果是使生產函式向上移動（或等效地，正如我們將看到的，使成本函式向下移動），它也可以改變生產函式的形狀，因為它可能會改變生產要素組合。

這可以用等產量圖來表示，如右側所示。

如果相對生產要素價格沒有發生變化，那麼技術變革可能不會導致新的擴張路徑，如果技術變革是要素中性的，那麼它只會使生產函式向上平行移動。如果技術變革不是要素中性的，那麼等產量曲線將改變形狀，因為生產要素的邊際產量將發生變化，因此將出現新的擴張路徑。

技術變革型別

長期 - 包括生產函式中的時間
創新 - 包括生產函式中的創新存在
設施 - 包括生產函式中設施的可用性

條件

一階條件（FOC）不足以定義最小值或最大值。

二階條件也是必需的。然而，如果生產集是凸的，並且投入成本函式是線性的，那麼FOC足以定義最大產出或最小成本。

參考文獻

供應鏈	運輸經濟學	成本
	生產