- 另見:效用應用於出行方式選擇 (交通基礎知識華夏公益教科書)
效用 是經濟學家對消費者試圖最大化的東西的表達。消費者可能想要更多的一種東西,而想要更少另一種東西。...
 無差異曲線
無差異曲線
需求取決於效用。效用函式表示一種將排名分配給不同組合的方法,使得更優選的組合排名高於不太優選的組合。效用函式可以用一般的方式表示為

其中  和
和  是商品(例如,旅行產生的淨收益)
是商品(例如,旅行產生的淨收益)
無差異曲線是消費者對之無差異的商品組合的軌跡。如果偏好滿足通常的規律性條件(下面討論),則存在一個效用函式  來表示這些偏好。無差異曲線上的點表示等效用。負斜率表示邊際替代率 (MRS)
來表示這些偏好。無差異曲線上的點表示等效用。負斜率表示邊際替代率 (MRS)

 替代品
替代品
 互補曲線
互補曲線
替代品將由

表示,其中無差異曲線的斜率 = -a/b。
從圖形上來說,替代性越大,無差異曲線越接近直線。完全替代性是直線無差異曲線(例如,透過模式 A 或模式 B 出行上班)。
互補品由以下表示

互補性越高,無差異曲線越接近直角曲線;完全互補性將具有直角無差異曲線(例如,左右鞋,從家到工作和從工作到家的旅行)
貿易遊戲是一種檢查資源的經濟交易如何影響個人效用的方法。假設經濟包含以下資源(用彩色紙片表示)
- 白色
- 紫色
- 棕色
- 橙色
- 藍色
- 灰色
- 綠色
- 黃色
- 金色
遊戲的目標是最大化你的效用收益。
為自己定義一個效用函式

你會得到各種各樣的資源
衡量你的效用
與班上的其他人進行交易(15分鐘) 記錄你的交易。
在交易期結束時再次衡量你的效用。計算你的絕對和百分比增長。
在黑板上記錄分數
討論
有沒有更好的資源分配方式?
 預算約束
預算約束
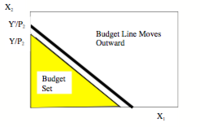 預算曲線向外移動
預算曲線向外移動
 預算曲線的斜率變化
預算曲線的斜率變化
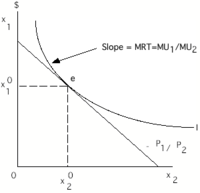 效用最佳化
效用最佳化
效用最大化涉及在資源約束下選擇商品組合。例如,個人透過比較消費增加帶來的效用增加與放棄資源(或等效地放棄這些資源可以購買的消費)帶來的效用損失,來選擇商品、服務和交通工具的數量。
通常將一個價格視為1,將一種商品視為貨幣。收入增加可以用預算線向外移動來表示。
商品 的價格上漲可以用預算線的斜率變化來表示(仍然固定在一個端點)。
的價格上漲可以用預算線的斜率變化來表示(仍然固定在一個端點)。
從圖形上來說,最佳化過程是透過將個人願意用一種商品交換另一種商品的比率與市場允許他/她進行交換的比率相等來實現的。這可以用下圖來表示
個人透過沿著預算約束線向下移動到預算線的斜率( )——這是市場規定的交換比率——正好等於個人願意用這兩種商品進行交換的比率來最大化效用。這就是無差異曲線的斜率或邊際轉換率(MRT)。像 'e' 這樣的點是一個效用最大化的均衡點。
)——這是市場規定的交換比率——正好等於個人願意用這兩種商品進行交換的比率來最大化效用。這就是無差異曲線的斜率或邊際轉換率(MRT)。像 'e' 這樣的點是一個效用最大化的均衡點。
均衡點是無差異曲線/效用曲線與預算約束線的切點。
作為一個最佳化問題,可以寫成

受以下條件約束

 在
在  中
中
其中
 = 價格向量,
= 價格向量, = 商品向量,
= 商品向量, = 收入
= 收入
(由於非飽和性,約束條件可以寫成 px=m。)這種問題可以用拉格朗日乘子來解決
 其中
其中
 是拉格朗日乘子
是拉格朗日乘子
對  求導,並將一階條件設為 0
求導,並將一階條件設為 0

除以獲得邊際替代率和經濟替代率






求解

或者

代入預算約束



馬歇爾需求將價格和收入與需求束聯絡起來。這表示為  。此函式是 0 次齊次函式,因此如果我們將
。此函式是 0 次齊次函式,因此如果我們將  和
和  都加倍,
都加倍, 保持不變。我們可以開發一個間接效用函式
保持不變。我們可以開發一個間接效用函式

受以下約束:
其中求解此方程的 X 是需求束

進行單調變換

隨收入增加而增加,隨價格下降而下降
其中求解此方程的  是需求束
是需求束
間接效用函式  的屬性
的屬性
- 在
 中非遞增,在
中非遞增,在  中非遞減
中非遞減
- 0 次齊次函式
- 在
 中擬凸
中擬凸
- 在所有

間接效用函式的逆函式是支出函式 
約束條件:
支出函式  的性質
的性質
- 在
 中非遞減
中非遞減
- 在
 中具有 1 次齊次性
中具有 1 次齊次性
- 在
 中是凹的
中是凹的
- 在
 中是連續的,對於
中是連續的,對於 
希克斯需求或補償需求用 h(p,u) 表示。

改變價格和收入以保持消費者在固定的效用水平,與馬歇爾需求相比。羅伊恆等式允許在觀察到的需求和效用之間來回轉換



 達到
達到  的最小支出為
的最小支出為 
 從收入
從收入  獲得的最大效用為
獲得的最大效用為 
 在收入為
在收入為  時期的馬歇爾需求與在效用為
時期的馬歇爾需求與在效用為  時期的希克斯需求相同。
時期的希克斯需求相同。
 在效用為
在效用為  時期的希克斯需求與在收入為
時期的希克斯需求與在收入為  時期的馬歇爾需求相同。
時期的馬歇爾需求相同。
貨幣度量間接效用函式表明在價格水平為 p 時需要多少資金才能與在價格水平為 q 且收入為 m 時擁有相同的效用。將其定義為


注意 1 表示變化後,0 表示變化前
以當前價格為基準,需要多少收入變化才能獲得相同的效用
 新的價格為基準,什麼收入變化可以補償價格變化
新的價格為基準,什麼收入變化可以補償價格變化
 效用和消費者剩餘
效用和消費者剩餘

通常

當效用是擬線性的 ( , 那麼
, 那麼

阿羅不可能定理 社會福利函式聚合問題的說明
三個個人都有良好的行為偏好。但是,將這三個聚合在一起並不會產生一個良好的行為偏好函式
- 甲喜歡紅色勝過藍色,藍色勝過綠色
- 乙喜歡綠色勝過紅色,紅色勝過藍色
- 丙喜歡藍色勝過綠色,綠色勝過紅色
聚合後,傳遞性被違反
- 兩個人喜歡紅色勝過藍色
- 兩個人喜歡藍色勝過綠色,
- 兩個人喜歡綠色勝過紅色
社會想要什麼?
定義一個消費集X,例如{房屋,汽車,電腦},
'x', 'y', 'z', 是商品組合,例如 x{房屋,汽車}, y{汽車,電腦}, z{房屋,電腦}。
商品本身並不被消費,而是為了相對於其他商品的屬性而被消費
我們想要找到對組合進行排序的偏好。效用是序數,所以我們只關心哪個更大,而不是大多少。
對偏好有一些條件,以產生一個連續(良好行為)的效用函式。
- 完備性:或者
 (讀作 x 比 y 更好)或者
(讀作 x 比 y 更好)或者  或者兩者都滿足
或者兩者都滿足
- 自反性:

- 傳遞性:如果
 並且
並且  ,那麼
,那麼  (這對社會福利函式構成了一個問題)
(這對社會福利函式構成了一個問題)
- 單調性:如果
 ,那麼
,那麼 
- 區域性非飽和:多總比少好
- 凸性:如果
 並且
並且  ,那麼
,那麼 
- 連續性:輸入的微小變化會導致輸出的微小變化。偏好關係
 在 X 中是連續的,如果它在極限運算下保持不變
在 X 中是連續的,如果它在極限運算下保持不變
如果函式 f 在其域中的點 a 處連續,則
 存在
存在

如果 'f' 在 'a' 處不連續,我們說 'f' 在 'a' 處不連續。













































































