三角學/愛好者/希爾伯特第三問題

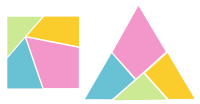
帽子商問題（右圖）由謎題創作者亨利·杜德尼於 1907 年提出，它將三角形切割成正方形，只需三刀。

任何兩個面積相同的二維多邊形都可以被切割成不同的碎片，使得其中一個可以被重新組合成另一個。罕見的是，這種切割方式如此優雅。當你不在乎碎片數量時，找到切割方案並不難。

證明我們可以將任何兩個面積相同的多邊形切割成相同的碎片。

注意，我們總是可以將多邊形切割成三角形。我們可以利用這個事實，只關注我們是否可以透過切割將一個三角形轉換成另一個面積相同的三角形。
如果你在嘗試將一個三角形轉換成另一個三角形時卡住了，這裡有一個可能的解決方案。在你嘗試過這個問題之後再看它。

希爾伯特第三問題是，兩個底面積和高都相同，因此體積也相同的四面體，是否可以被切割成四面體並重新組合成彼此。對於某些四面體對來說是可能的，但並非所有都如此。一個非常密切相關的問題是，一個立方體是否可以被切割成有限數量的碎片並重新組合成一個正四面體。事實證明，這是不可能的。

為了證明這一點，我們需要一些數學工具。

向量空間

在本頁中，我們將使用有關向量空間的概念。

實數上的向量空間

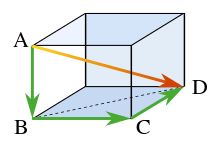
處理三維空間的一種數學方法是將其作為三維歐幾里得空間 $\mathbb {R} \times \mathbb {R} \times \mathbb {R}$ ，也可以寫成 $\mathbb {R} ^{3}$ 。空間中的一個點由三個數字表示，每個數字都是一個實數，比如 $\displaystyle 3$ 或者 $\displaystyle 6.18239013...$ 或者 $\displaystyle 1.414...$

對於 $\mathbb {R} ^{3}$ ，我們可以使用勾股定理計算距離 - 將每個座標的平方加起來，然後取平方根。

也有一些公式可以計算不同方向之間的角度，以及各種型別的三維空間位置變換，例如繞原點旋轉。 $\mathbb {R} ^{3}$ 是一個我們對事物如何運作有很大直覺的空間。

我們不必將自己侷限於三維空間。我們可以擁有 $\mathbb {R} ^{109}$ 上的向量空間。許多關於 $\mathbb {R}$ 上向量空間的公式，無論是在 1、2、3 維還是更高維中，都適用。在這些情況下，用 $\mathbb {R} ^{n}$ 表述結果更經濟，其中我們理解可以自由選擇 n 的值。即使如此，我們通常使用 $\mathbb {R} ^{3}$ 而不是 $\mathbb {R} ^{109}$ 來幫助我們理解正在發生的事情。

關於向量空間的更多資訊可以在《線性代數》一書中找到。
維基百科也提供了關於歐幾里得空間的資訊。

有理數上的向量空間

我們也可以在有理數上形成一個向量空間， $\mathbb {Q}$ 。

$\mathbb {Q}$ 包括像 $\displaystyle 1.3$ 這樣的數字（它可以表示為有理數分數 $\displaystyle 13/10$ ），但不包括像 ${\sqrt {2}}=1.4142...$ 或 $\displaystyle 6.18239013...$ 這樣的數字，我們假設 '...' 表示它以任意數字繼續下去， $6.18239013...\notin \mathbb {Q}$ 。

在 $\mathbb {Q} ^{3}$ 中，座標為 $\displaystyle (4.5,-7.1,9/7)$ 的點是允許的。座標為 $\displaystyle (9.2,6.18239013...,8.1)$ 的點是不允許的，因為所有三個座標都必須在 $\mathbb {Q}$ 中。

$\mathbb {Q}$ '遺漏了一些值' 這一事實對我們來說將非常重要，因為它將證明我們無法解剖任意四面體並重新組裝成一個立方體。

無論我們使用 $\mathbb {R} ^{3}$ 還是 $\mathbb {Q} ^{3}$ ，我們使用“點”來表示相對於原點的位姿，並使用向量來表示兩點之間的相對位移。我們可以對向量進行加法運算。我們可以對向量進行減法運算。我們可以用一個數字乘以一個向量，前提是該數字是正確的型別（在 $\mathbb {R}$ 或 $\mathbb {Q}$ 中分別為實數或有理數）。

為了研究希爾伯特的第三問題，我們需要一個關於 $\mathbb {Q}$ （有理數）的向量空間。像 $\displaystyle 3/4$ 和 $\displaystyle -1.125$ 這樣的數字是允許的。像 $\displaystyle 6.18239013...$ 這樣的數字是不允許的。

商空間

解釋什麼是商空間

不變數

多米諾骨牌

一個非常有用的工具，用於證明一個圖形不能以特定方式細分，就是不變數的概念。它們可以用於例如多米諾骨牌問題中證明不可行性。

這裡有一個簡單的分割或細分謎題，其中一個不變量表明為什麼解是不可行的。

在這個謎題中，目標是用 23 個多米諾骨牌（只有兩個方格的多米諾骨牌）平鋪選定的區域。

這是不可能的。

為什麼平鋪不能起作用（劇透）

劇透警告：我們即將給出簡單而優雅的證明。如果您想先自己嘗試一下，請停止閱讀。如果不是，請繼續閱讀。如果我們將棋盤像棋盤一樣著色，例如左上角為黑色，那麼黑色方格比白色方格多兩個。然而，每個多米諾骨牌覆蓋一個白色方格和一個黑色方格。

黑色方格覆蓋數與白色方格覆蓋數之差是一個不變數。它在空棋盤上的初始值為零。當我們放置更多多米諾骨牌時，不變數保持不變。它確實是常數。它從零開始，並保持為零。然而，為了覆蓋所有方格，它需要達到 2 - 這產生了矛盾。

其他不變數

在多米諾骨牌問題中，不變數只是一個數字。為了解決希爾伯特的第三問題，我們需要一個更復雜的不變數。我們需要一些能夠同時捕捉角度和長度資訊的東西。你可能認為複數可以滿足要求，但實際上我們需要更多，因為涉及的長度不止一個。我們以一種專門針對我們正在解決的問題的方式構建了不變數的定義域。該定義域不是 R，也不是 C，而是一個我們構建的相當奇怪的數學物件，它正好具有我們需要的性質。

張量積

解釋什麼是張量積

德恩不變數

\operatorname {D} (P)=\sum _{e}\ell (e)\otimes (\theta (e)+\mathbb {Q} \pi )

它是常數

證明，由於我們以這種方式構建了它，因此當我們將多面體切成碎片時，它不會改變。