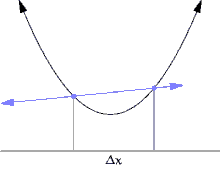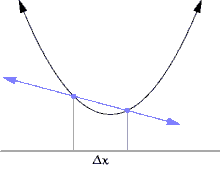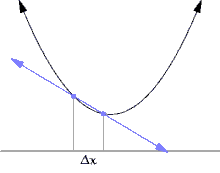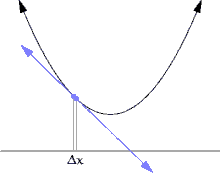
 切線的斜率可以用逼近切線的割線來近似。
切線的斜率可以用逼近切線的割線來近似。
曲線上的一個點的斜率等於該點切線的斜率。由於直接測量切線的斜率很困難,我們使用割線來近似它。割線是在曲線上的兩個點之間的一條線。
假設我們想要找到座標為 的點的斜率。我們可以使用經過
的點的斜率。我們可以使用經過 和
和 的割線來近似它,其中
的割線來近似它,其中 是
是 的一個微小變化,而
的一個微小變化,而 是由此產生的
是由此產生的 的微小變化。
的微小變化。
割線的斜率為 。當
。當 越來越小時,
越來越小時, 接近點
接近點 的斜率。
的斜率。
當  趨近於零時,
趨近於零時, 的 極限 是我們所要找的值:點
的 極限 是我們所要找的值:點  的梯度。對於任意點
的梯度。對於任意點  ,梯度可以用導數表示。
,梯度可以用導數表示。
函式  的 導數
的 導數  是一個函式,它提供了
是一個函式,它提供了  所產生的曲線在點
所產生的曲線在點  的梯度。導數的正式定義為
的梯度。導數的正式定義為 
表示函式導數主要有兩種方式: 和
和  。它們都表示相同的意思:
。它們都表示相同的意思: 關於
關於  的導數。
的導數。
以下是一些簡單的規則,可以使複雜表示式的求導更容易。

例如,

例如,

例如,

例如,
切線是一條經過給定點的直線,它的斜率等於曲線在該點的斜率。法線是一條經過給定點的直線,它垂直於曲線在該點的切線。
要找到曲線在特定點處的切線或法線的方程,我們可以使用我們在座標幾何中使用的直線方程。
例如,求曲線 在點
在點 處的切線和法線的方程。
處的切線和法線的方程。

遞增函式是指斜率始終大於或等於零的函式。
遞減函式是指斜率始終小於或等於零的函式。
一個量的變化率是指該量關於時間的導數。例如,如果水以每秒 1 升的速度流入桶中,那麼桶中水量的變化率就是每秒 1 升。
在某些情況下,兩個量的變化率是相互關聯的。例如,一個半徑變化的圓將具有一個取決於半徑的變化面積。圓的面積與半徑的關係為  。如果半徑以每秒 3 釐米的速度增長,它的變化率為
。如果半徑以每秒 3 釐米的速度增長,它的變化率為  。可以使用鏈式法則求出面積的變化率
。可以使用鏈式法則求出面積的變化率

如果半徑以每秒 3 釐米的速度增長,並且當前為 5 釐米,則面積的變化率為  平方釐米/秒。
平方釐米/秒。
 圖上最大值和最小值的一個例子
圖上最大值和最小值的一個例子
駐點是指曲線上的斜率為零的點。這意味著該點處的函式導數等於零。
駐點要麼是最大值,要麼是最小值。最大值是指函式達到最大值的地方。最小值是指函式達到最小值的地方。我們可以透過檢視二階導數來確定駐點是最大值還是最小值。
如果二階導數為正,則斜率隨著輸入的增加而增加,因此駐點是極小值。
如果二階導數為負,則斜率隨著輸入的增加而減小,因此駐點是極大值。
繪製曲線圖時,駐點很有用。透過標記駐點,我們可以比其他方法更準確地繪製圖形。
← 級數 · 積分 →































