代數/函式

代數

另見: 微積分/函式, 離散數學/函式和關係

---

函式作為盒子

函式是另一種用數學方法描述某些事物的途徑。它們通常被描述為一個兩端開口的盒子中的機器；你從一端放入一些東西，在中間發生一些事情，然後從另一端出來一些東西。函式是盒子內部的機器，它由它對任何輸入執行的操作定義。

假設機器有一個刀片，它會將你放入的任何東西切成兩半，並將其中一半從另一端送出。如果你放進去一根香蕉，你就會得到半根香蕉。如果你放進去一個蘋果，你就會得到半個蘋果。

關於這臺機器的一個好問題可能是，另一半水果發生了什麼？但是，由於這是代數，進入和走出函式的東西將是數字，因此我們很確定盒子不會被數字填滿並破裂。讓我們將該函式定義為接受你的輸入並將其切成兩半，即除以二。如果你放入 2，你將得到 1。如果你放入 57，你將得到 28.5。函式機器允許我們改變表示式。函式通常用單個字母命名。我們將這個叫做 h，代表 half（一半）。（我們選擇的字母沒有什麼特別之處——我們也可以稱這個函式為 f。這個字母不必代表任何東西。）

現在我們需要符號。要將 2 放入函式中，我們寫 $h(2)$（讀作 h of 2）。我們知道

$h(2)=1$

我們還可以計算

$h(57)=28.5$

使用代數符號，我們可以描述這臺機器的功能為

$h(x)={\frac {x}{2}}$

與其列出我們可以放入機器的所有東西，我們用變數 $x$ 來表示它們。當我們寫 $h(x)$ 時，我們的意思是我們將 $x$ 送入機器，它被切成兩半。使用這種形式，我們不必計算當我們放入 57 個蘋果或橘子時從機器出來的半數。我們知道，當我們將 57 或任何東西放入我們的機器時，只有 28.5 這些東西會從另一端出來。當使用代數符號來指定關係時；我們建立了一些稱為代數函式定義的東西。（這個例子說明了數學與科學和工程之間的區別。由於這是一個假想的機器，我們只需要指定從盒子另一端出來的是什麼。在真實的機器中，我們還需要考慮如何處理沒有從另一端出來的部分）。

練習題

在指數中使用 ^

對於第 1-6 題，使用代數來定義所描述的函式。

Example: x) Three-quarters of a number
 Answer: $f(x)=3x/4$

 

1 一個數字的五分之四

2 一個數字加上它自身的五倍

3 一個數字加上該數字的三倍

4 一個數字乘以它自身七次，然後減去該數字

5 一個數字減去另一個數字的三倍

6 一個數字的一半乘以另一個數字加三

將數字透過函式盒的過程稱為對該數字求函式值。對於第 7-22 題，求出給定數字的所描述函式的值。

Example: x) $f(x)=3x-4$
 a) $f(0)$ b) $f(4)$
 c) $f(1/3)$  d) $f(1/2)$
 
 Answer: a) $f(0)=3(0)-4=-4$   b) $f(4)=3(4)-4=8$
 c) $f(1/3)=3(1/3)-4=-3$ d) $f(1/2)=3(1/2)-4=-5/2$

 

$f(x)=10x$

7

$f(1)=$

8

$f(1/2)=$

9

$f(3.5)=$

10

$f(-1)=$

$g(x)=3x-1$

11

$g(4)=$

12

$g(2/3)=$

13

$g(1.1)=$

14

$g(-3)=$

$h(x)=x^{2}$

15

$h(7)=$

16

$h(3/5)=$

17

$h(5.3)=$

18

$h(-6)=$

$i(x)=1/(x-4)$

19

$i(5)=$

20

$i(2/3)=$

21

$i(7.25)=$

22

$i(0)=$

函式作為關係

函式也可以被認為是關係的子集。關係是集合中數字之間的聯絡。

換句話說，你輸入的每個數字都與你輸出的每個數字相關聯。區別在於在函式中，每個“輸入”數字都與一個“輸出”數字相關聯，而在關係中，“輸入”數字可能與多個或零個“輸出”數字相關聯。這是關於函式的一個重要事實。請注意，上面圖表中所示的關係不是函式，因為它不滿足此要求，不像下面第二個圖表中所示的關係，它是一個函式。

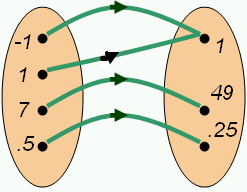
所有函式都是關係。並非所有關係都是函式。

練習題

以下哪些定義是函式，哪些是關係

1 $f(x)=x+2$

	函式
	關係

2 $g(x)=x-2$

	函式
	關係

3 $h(x)=x*2$

	函式
	關係

4 $i(x)=x/2$

	函式
	關係

以下哪些定義是函式，哪些是關係

5 $j(x)=x+x$

	函式
	關係

6 $k(x)=x-x$

	函式
	關係

7 $l(x)=x*x$

	函式
	關係

8 $m(x)=x/x$

	函式
	關係

9 你能描述問題 1-8 中的函式嗎？它們有什麼區別？(請在紙上作答)

定義域和值域

定義域

函式的定義域是指該函式定義的“輸入”數字的集合。定義域是函式定義的一部分。在上圖中的函式中，定義域是{-1,1,7,1/2}。

自然定義域是指代數定義的函式中，函式定義的數字的集合。

在大多數代數公式中，x 通常是與定義域相關的變數。

例子

函式 $f(x)={\sqrt {x}}$ 的定義域是 $x\geq 0$，因為平方根函式僅在正數時有定義（假設我們只處理實數）。

值域

函式的值域是指對於給定輸入，方程的結果或解的集合。一個真正的函式對於每個定義域值只有一個結果。

在大多數代數公式中，y 通常是與值域相關的變數。因此，它也可以表示為f(x)，表示它的值是x 的函式。

例子

函式 $f(x)=x^{2}$ 的值域是 $y\geq 0$，因為數字的平方總是正數。

從定義域和值域的角度看函式

同時考慮定義域和值域，函式是指任何數學公式，對於每個輸入值都產生一個且僅一個結果。因此，可以說在一個有效的函式中，定義域 (x) 和值域 (y) 具有多對一的關係，因此對於每個給定的定義域值，只有一個值域值作為結果，但反過來不一定如此。這是有道理的，因為結果可以重複，但輸入不能重複。

因此，如果 x 是水平方向，y 是垂直方向，那麼以 y 為自變數的函式（例如 y = mx + b）將產生一組結果，使得如果在 圖 上的任何點處用垂直線與之相交，它將只穿過圖形一次。漸近函式（至少有一個未定義結果）也被認為是有效的，因為它沒有穿過圖形的多個點。這被稱為“垂直線”測試。

定義域和值域這兩個術語可以應用於所有關係，而不僅僅是函式。關係是指在一個定義中，定義域中的一個元素對映到值域中的多個元素。我們使用定義域和值域這兩個術語來定義函式和關係之間的區別。

函數術語

在談論或書寫函式時，不同的術語被用來描述函式如何工作或它們的功能。

f of x 術語

當我們寫 $f(x)$ 時，我們說 f of x。因此，如果我們有一個用方程 $g(x)={\frac {x+2}{7}}$ 定義的函式，那麼我們說

g of x 等於 x 和 2 的和除以 7。
或者
g of x 是 x 加 2 全部除以 7。

當我們將一個值（比如 5）代入函式中的 x 時，我們寫 $g(5)={\frac {5+2}{7}}={\frac {7}{7}}=1$，但我們說

g of 5 等於 1.

代數符號是數學家表達由算術運算子定義的關係的最簡單方法，如 $+,-./*,$ 指數和根式。一旦定義了其中一些函式，用函式名和上述函式值進行引用就更容易了。

函式 "value of" 術語

如果我們有一個用方程 $g(x)={\frac {x+2}{7}}$ 定義的函式，那麼我們說 g 在 x 處的函式值是 x 和 2 的和除以 7。 這樣，$g(5)={\frac {5+2}{7}}={\frac {7}{7}}=1$

分段函式

一個函式，其定義取決於輸入。

絕對值函式

f(x)=|x|
或者
$f(x)={\begin{cases}x&{\mbox{if }}x\geq 0\\-x&{\mbox{if }}x<0\end{cases}}$

可以將 $|x|$ 解釋為 x 和 0 之間的無向距離（始終是非負的）。繼續，$|x-y|$ 可以解釋為數軸上數字 x 和 y 之間的距離。

偶函式和奇函式

偶函式

偶函式定義為一個函式 $f$，滿足 $f(-x)=f(x)$。
從幾何意義上講，偶函式可以定義為關於 y 軸（穿過原點的垂直線）具有映象對稱性的函式。

偶函式的一個例子是 $h(x)=x^{2}$，因為 $f(5)=25=f(-5)$，並且因為對於所有實數 x，都有 $f(x)=x^{2}=f(-x)$。

奇函式

奇函式定義為一個函式 $f$，滿足 $f(-x)=-f(x)$。
從幾何意義上講，奇函式可以定義為關於原點具有 180 度旋轉對稱性的函式。

一個 奇 函式的例子是 $f(x)=x^{3}$，因為對於所有實數 x，都有 $f(x)=x^{3}=-((-x)^{3})=-f(-x)$，例如 $f(2)=2^{3}=8=-((-2)^{3})=-(-8)=-((-2)^{3})=-f(-2)$

複合函式

複合函式 $h$ 可以定義為兩個函式 $f$ 和 $g$ 的複合，記為 $h(x)=f(g(x))$ （讀作 h of x 等於 f of g of x）或 $h(x)=(f\circ g)(x)$。

例子

Let $f(x)=2x+1$     $g(x)=5x-3$
 $h(x)=f(g(x))$
 $h(x)=f(5x-3)$
 $h(x)=2(5x-3)+1$
 $h(x)=10x-6+1$
∴$h(x)=10x-5$

例子

Let $f(x)=-{\sqrt {16-x}}\,$     $g(x)=4x^{2}\,$
$(f\circ g)(x)=f(4x^{2})\,$
$(f\circ g)(x)=-{\sqrt {16-(4x^{2})}}\,$
$(f\circ g)(x)=-{\sqrt {4(4-x^{2})}}\,$
$(f\circ g)(x)=-{\sqrt {4}}{\sqrt {(4-x^{2})}}\,$
$(f\circ g)(x)=-2{\sqrt {4-x^{2}}}\,$
Domain: $-2\leq x\leq 2$
Range: $-4\leq y\leq 0$

反函式

函式 $g$ 是一個一對一函式 $f$ 的反函式，當且僅當以下條件成立

$g(f(x))=x\,$

$f(g(x))=x\,$

函式 $f$ 的逆函式用 $f^{-1}$ 表示。

從幾何角度來看，$f^{-1}$ 是 $f$ 關於直線 $y=x$ 的映象。從概念上講，使用 *盒子* 類比，函式的逆函式盒子 *撤銷* 函式常規盒子的操作。

例子

$f(x)=2x\,$
$f^{-1}(x)={\frac {1}{2}}x\,$

$f(f^{-1}(x))=f({\frac {1}{2}}x)\,$
$f(f^{-1}(x))=2({\frac {1}{2}}x)\,$
$f(f^{-1}(x))=x\,$


$f^{-1}(f(x))=f^{-1}(2x)\,$
$f^{-1}(f(x))={\frac {1}{2}}(2x)\,$
$f^{-1}(f(x))=x\,$

要找到函式的逆函式，請記住，當我們使用 $f^{-1}(x)$ 作為 $f$ 的輸入時，結果是 $x$。因此，首先寫下 $x=f\left(f^{-1}(x)\right)$ 並求解 $f^{-1}$。

例子

Suppose:$f(x)=2x+1\,$
Then $x=f\left(f^{-1}(x)\right)$
$x=2f^{-1}(x)+1\,$
$x-1=2f^{-1}(x)\,$
$f^{-1}(x)={\frac {x-1}{2}}\,$

逆函式的定義域與原函式的值域完全相同。如果原函式的值域受到某種限制，則逆函式需要一個受限的定義域。

例子

$f(x)={\sqrt {x-1}}\,$         
$x=f\left(f^{-1}(x)\right)$
$x={\sqrt {f^{-1}(x)-1}}\,$         
$x^{2}={\sqrt {f^{-1}(x)-1}}^{2}\,$         
$x^{2}=f^{-1}(x)-1$            
$f^{-1}(x)=x^{2}+1\,$            
The Range of $f(x)$ is $f(x)\geq 0$. So the Domain of $f^{-1}(x)$ is $x\geq 0$.

一一函式

對於每個輸入都存在一個唯一輸出的函式。

等價地，我們可以說函式 $f$ 被稱為 *一一函式*，如果對於所有 $x,x'\in A,f(x)=f(x')$ 意味著 $x=x'$，其中 *A* 是 *f* 的定義域集合，*x* 和 *x'* 都是該集合的成員。

水平線測試
如果沒有任何水平線與函式圖交於一個以上的位置，則該函式為一一函式。

建立函式

在上一章中，我們回顧了你已經瞭解的數學知識：數字、變數和關係。我們回顧了數字的型別、對數字可以執行的操作、這些操作的性質以及這些性質如何讓你寫出表示式，或者如果我們對錶達式足夠了解，你可以寫出定義真實事物的方程和不等式。

在上面的部分中，我們已經瞭解了函式的概念。首先，我們展示瞭如何在等號運算子的一側建立函式，而在另一側建立表示式。然後，我們查看了使用函式符號的更復雜方法。

一旦你習慣了它們，函式就會讓你以不同的方式看待數學。當你用數字思考數學時，你只是在思考一個答案。當你用函式思考數學時，你是在尋找關係，並且你在建立數學模型。

舉一個 3x3 平方格和對角線的例子。對角線上的三角形面積是多少？應用面積函式：l x w，然後應用一半函式。