代數/函式影像

代數

函式具有自變數和因變數

當我們看到一個像  $f(x)={\frac {1}{2}}x,$  這樣的函式時，我們稱我們正在改變的變數——在本例中是  $x\,$ --為自變數。我們將函式的值賦給一個我們稱為因變數的變數。我們說  $x\,$  是自變數的原因是，我們可以為函式定義的任何值選擇——在本例中是實數  $\mathbb {R}$  是隱含的——作為函式的輸入。一旦我們選擇自變數的值，函式就會始終輸出相同的結果。我們說結果被賦予因變數，因為它取決於我們放入函式中的值。

將  $y\,$  與我們的函式  $y={\frac {1}{2}}x,$  等同，則  $2y=2({\frac {1}{2}}x),$  則  $2y=x,\,$  則  $g(y)=2y.\,$

自變數現在是  $y\,$  而因變數是  $x.\,$

• 注意：這是一個非常不常見的情況，其中有序對  $(g(y),y)\,$  被反向對映  $y\mapsto x\,$  以及相應的反轉（因變數，自變數），（值域，定義域），現在  $x\,$  必須對於每個  $y\,$  都是唯一的，對應於函式的水平線檢驗！旋轉或交換軸的位置、座標對  $(x,y)\,$  和（橫座標，縱座標）的順序將是不好的。

我們是否使用了代數來改變函式的性質？讓我們看看三個函式的結果

$f(x)={\frac {1}{2}}x$	$g(y)=2y\,$	$h(x)=2x\,$
$x\,$   $f(x)\,$     $2\,$     $1\,$     $0\,$     $0\,$   $-2\,$   $-1\,$	$y\,$   $g(y)\,$     $1\,$     $2\,$     $0\,$     $0\,$   $-1\,$   $-2\,$	$x\,$$x\,$   $h(x)\,$     $1\,$     $2\,$     $0\,$     $0\,$   $-1\,$   $-2\,$

如果我們觀察上面的表格，我們可以看到 $f(x)\,$  的自變數給出的結果與 $g(y).\,$  的因變數相同。當我們檢視 $h(x).\,$  的值時，我們可以看到這意味著什麼。函式 $g(y)\,$  與函式 $f(x),\,$  相同，但是當我們在 $g(y)\,$  和 $h(x)\,$  之間切換我們使用的自變數時，我們發現 $g(y)\,$  和 $h(x)\,$  是互逆函式。

讓我們看看如何在 $x\,$  和 $y\,$  中繪製函式，然後回過頭來再次看看自變數和因變數的概念。

顯函式和隱函式

諸如 $x\,$  和 $y\,$  這樣的變數，可以使用簡單的代數來構成一個“關係”。 $f,\,$   $g,\,$  和  $h\,$  通常用來表示函式。函式記號 $f(x),\,$  讀作“f of x”，表示一個對自變數 $x.\,$  具有“顯式”依賴關係的函式。透過將變數 $y\,$  賦值為 $f(x),\,$   $y=f(x),\,$   $y\,$  現在就成為使用方程記號表示的  $x\,$  的“隱式”函式。如果 $f(x)\,$  是 ${\frac {x}{2}},$  那麼 $y={\frac {x}{2}}$   [ $y(x)\,$  將表示 $x\,$  的“顯式”函式]。當因變數對於每個自變數值都只有一個值時，關係也是一個函式。

笛卡爾座標系

The Cartesian Coordinate System is a uniform rectangular grid used for plane graph plots. It's named after pioneer of analytic geometry, 17th century French mathematician René Descartes, whose Latinized name was Renatus Cartesius. Recall that each point has a unique location, different from every other point. We know that a line is a collection of points. If we pick a direction of travel for the line that starts at a point then all of the other points can be thought of as either behind our starting point or ahead of it. Finally, a plane can be thought of as a collection of lines that are parallel to each other. We can draw another line that is composed of one point from each of the lines that we chose to fill our plane. If we do this then we can locate the other lines as behind or ahead of the line with the point we chose to start on. Descartes decided to pick a line and call it the  $x\,$ -axis, and to then pick a line perpendicular to this line and call it the  $y\,$ -axis. He then labeled this intersection point  $(0,0)\,$  and origin O. The points to the left (or behind) of this point each represent a negative number that we label as  $(-x,0).\,$  The points to the right (or ahead) of this point each represent a positive number that we label as  $(x,0).\,$  The points on the  $y\,$ -axis that are above  $0,0\,$  are labeled as positive  $(0,y),\,$  and the points on the  $y\,$ -axis below  $0,0\,$  are labeled as negative  $(0,-y).\,$  A point is plotted as a location on the plane using its coordinates from the grid formed by the  $x\,$  and  $y\,$ -axes. If you draw a line perpendicular to the  $x\,$ -axis from a point you pick then that point has the same  $x\,$ -coordinate as the point where that line crosses the  $x\,$ -axis. If you draw a line perpendicular to the  $y\,$ -axis from your point then it has the same  $y\,$ -coordinate as the point where that line crosses the  $y\,$ -axis. If you need to sharpen your knowledge in this area, this link/section should help: The Coordinate (Cartesian) Plane

方程及其圖形可以被認為是相等的。這是正確的，因為圖形是特定方程的表示。這是因為方程是由一個或多個變數以及一個或多個數字和一個等號組成（ $x=1,\,$  $y=x+1,\,$  以及  $y=x^{2}+2x+1\,$  都是方程的例子）。由於變數被引入作為表示可以代入方程的許多可能數字的一種方式。方程的圖形是繪製可以輸入的數字（自變數）和可能產生的輸出之間關係的一種方式。例如，在方程中： $y=x+2,\,$  我們可以選擇使  $x\,$  成為自變數，並且輸出數字每次都將比輸入數字大二。該方程的圖形將是顯示此關係的圖片。在圖形上，每個  $y\,$ -值（縱軸）將比代入的（橫向）  $x\,$ -值高二，因為方程中的  $+\,2\,$  。

線性方程和函式

本節展示了我們可以用代數方法寫出線性函式的不同方法。我們將花一些時間來研究一種稱為“斜率截距式”的方法，其方程為  $y=f(x)=mx+b\,.\,$

• 線性方程和函式

除非另有說明  $x\,$  的定義域，否則將假定線性函式的定義域為所有實數  $\mathbb {R}$  ，因此所有線性函式的圖形中的直線都無限地向兩個方向延伸。此外，在所有實數定義域的線性函式中，線性函式的值域可以覆蓋  $y\,,\,$  的整個實數集，一個例外是當斜率  $m=0\,$  並且函式等於一個常數時。在這種情況下，值域只是該常數。另一種情況是平方函式，當  $b=0\,.\,$ 時，值域是非負的。

y截距常數b

結果表明， $y=f(x)=mx+b\,$  有無限個解（在英國， $y=mx+c\,;\,$  也很常見 $y=ax+b\,,\,$  $y=a_{1}x+a_{0}\,$  以及 $y=-{\frac {A}{B}}x-{\frac {C}{B}}\,$）。點 $(x,y)\,$  將被對映到自變數 $x\,$  （假設為橫軸）和 $y\,$  （假設為縱軸）在笛卡爾座標系上。透過給 $x\,$  賦值並計算 $y\,,\,$  即可找到一個（單個）點座標解。當 $x=0\,,\,$  時，根據零積性質，項 $m\times x=0\,$，根據加法單位元，項 $0+b=b=y\,.\,$。點 $(0,b)\,$  是直線（線性方程的解）中唯一與y軸相交的點。更多關於截距的連結： The  $x\,$  和  $y\,$  截距

當我們有方程$y=f(x)=mx+b\,$ 時，m告訴我們什麼？

$m\,$  是一個常數，稱為直線的斜率。斜率表示直線的傾斜程度。

斜率

任意兩個不同的點都可以確定一條唯一的直線，並且這條直線包含這兩個點。將本研究限制在平面幾何（$R^{2}$）內，併為唯一點固定座標，例如  $(x_{1},y_{1})\,$  和  $(x_{2},y_{2})\,$  ，則一條直線就被定義為兩個變數之間的關係，它可以用線性方程表示，並可以在圖上繪製。當這兩個點重合時，即使在同一個平面上，也會產生無限條直線。當  $x_{1}=x_{2}\,$  時，定義的是一條垂直線的關係，而不是一個函式。函式是計算結果為唯一因變數的方程關係。只有當（當且僅當）  $x_{1}\neq x_{2},\,$  時，包含這兩個點的直線才是  $x.\,$ 的線性“函式”。

對於線性函式，可以透過直線上任意兩個已知點確定其斜率。斜率對應於直線上任意兩個不同點之間垂直方向的增量或變化量除以水平方向的相應增量或變化量。
設 $\Delta y=\,$ 為 $y\,$ 方向（垂直方向）上的增量或變化量，以及
設 $\Delta x=\,$ 為 $x\,$ 方向（水平方向）上的增量或變化量。
對於兩個點  $(x_{1},y_{1})\,$  和  $(x_{2},y_{2}),\,$  ，函式直線的斜率 m 由下式給出： $m={\frac {\Delta y}{\Delta x}}={\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}$

• 此公式稱為斜率測量的公式，有時也稱為斜率公式。

對於線性函式，固定直線上兩個唯一的點或固定斜率和直線上任意一點就足以確定這條直線，並用方程表示它。線性函式有一種方程形式，稱為直線的點斜式²，它使用斜率  $m\,$  和任意一點  $(x_{1},y_{1})\,$  來確定函式直線的有效方程： $y-y_{1}=m(x-x_{1})\,$
代數/斜率

勾股定理和距離公式

線性方程的其他形式？

代數/標準式和求解斜率

直線的截距式

我們將介紹另一種線性函式的一般形式。這就是直線的**截距式**，其中常數a和b使得(a,0)是x截距點，(0,b)是
y截距點。

${\frac {x}{a}}+{\frac {y}{b}}=1\qquad$    其中a ≠ 0且b ≠ 0

常數a和b都不能等於0，因為不允許除以0。當線性函式具有簡化形式y = m x時，不能應用直線的截距式，因為
y截距縱座標不能等於0。

用常數a和b乘以直線的截距式將得到

$bx+ay=ab\$

然後它等價於一般線性方程形式A x + B y + C，其中A = b，B = a，C = ab。現在我們看到A和B都不能為0，因此截距式不能表示水平線或垂直線。僅用b乘以直線的截距式得到

${\frac {b}{a}}x+y=b$

如果我們減去

${\frac {b}{a}}x$

我們得到

$y=b-{\frac {b}{a}}x$

這反過來可以重新排列為

$y=-{\frac {b}{a}}x+b$

這等價於斜截式，其中斜率m = -b/a。

---

示例：一條繪製的直線在x軸上與-3相交，在y軸上與-6相交。什麼方程可以表示這條直線？斜率是多少？

解答：截距式：$\qquad {\frac {x}{-3}}+{\frac {y}{-6}}=1$

乘以-6得到${\frac {-6}{-3}}x+y=-6$

$y=-2x-6\$

所以我們看到斜率m = -2。

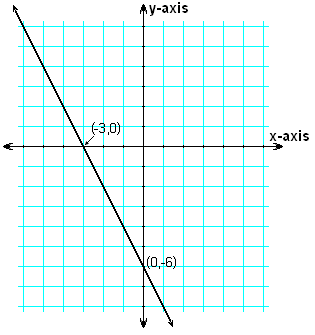     y = - 2x – 6的圖形，顯示截距。

該直線也可以寫成$-6x-3y=(-3)(-6)\$

$6x+3y=-18\$

---

示例：方程

${\frac {x}{2}}+{\frac {y}{4}}=0$

能否轉換為直線的截距式(x/a) + (y/b) =1來求截距？

解答：不能，任何有效的數學運算都不能將其轉換為截距式。而是乘以4，然後減去2x得到

$y=-2x\$

它具有y = m x的形式，其中m = -2。該直線與軸在(0,0)處相交。由於截距均為0，因此不能使用直線的一般截距式。

---

示例：求連線點(2,1)和(4,4)的直線的斜率和函式。

解答：當根據上述公式從兩點計算直線的斜率時，哪一個是點1，哪一個是點2並不重要。讓我們將(x₁,y₁)設為(2,1)，將(x₂,y₂)設為(4,4)。然後使用兩點斜率公式m

$m={\frac {4-1}{4-2}}={\frac {3}{2}}$

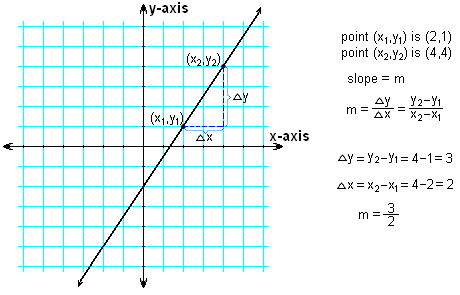
使用點斜式

將任一點的座標代入點斜式作為x₁和y₁。為簡單起見，我們使用x₁=2和y₁=1。

$y-1={\frac {3}{2}}(x-2)$

$y-1={\frac {3}{2}}x-3\,$

$\ y={\frac {3}{2}}x-2$

---

使用斜截式

或者，可以在一個變數的線性函式的一般形式y = m x + b中求解y截距縱座標b。

$b=y-mx\$

已知斜率m，取直線上任意一點，並將該點的座標和m代入線性函式的這種形式，計算b。在本例中，使用(x₁,y₁)。

$b=y_{1}-mx_{1}\,$

$b=1-{\frac {3}{2}}\cdot 2=1-3=-2$

現在常數m和b都已知，函式寫成

$y={\frac {3}{2}}x-2$      或寫成      $f(x)={\frac {3}{2}}x-2$

__________例題結束__________

有關斜率的另一種解釋，請參見此處

斜率

---

例題：畫出方程5x + 2y = 10的影像並計算斜率。

解答：這符合線性方程的一般形式，因此找到兩個不同的點足以確定直線。要找到x截距，令y = 0並解出x。

$5x+2\cdot 0=10=5x\$

$x=10/5=2\$

所以x截距點為(2,0)。要找到y截距，令x = 0並解出y。

$5\cdot 0+2y=10=2y\$

$y=10/2=5\$

所以y截距點為(0,5)。過(2,0)和(0,5)畫一條直線，就會得到以下圖形。

5x + 2y = 10的影像，顯示了截距

要從這兩點確定斜率m，可以將(x₁,y₁)設為(2,0)，(x₂,y₂)設為(0,5)，反之亦然，並按如下方式計算

$m={\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}={\frac {5-0}{0-2}}=-{\frac {5}{2}}=-2.5$

__________例題結束__________

直線的一般方程形式總結

適用於二維笛卡爾座標系上所有直線的最一般形式是

$Ax+By=C\$

其中包含三個常數 A、B 和 C。這些常數對於直線來說不是唯一的，因為將整個方程乘以一個常數因子會得到一組新的有效常數，它們對應於同一條直線。當 B = 0 時，方程的其餘部分表示一條垂直線，它不是函式。如果 B ≠ 0，則該直線為函式。這種線性函式可以用**斜截式**表示，斜截式包含兩個常數。

斜截式

$y=mx+b\$

這兩個常數 m 和 b 共同唯一地確定一條直線。換句話說，一條特定的直線在這種形式下只能有一對 m 和 b 的值。

這裡給出的**點斜式**

$y-y_{1}=m(x-x_{1})\,$

使用了三個常數；m 對於給定直線是唯一的；x₁ 和 y₁ 不是唯一的，可以是直線上任意一點的座標。點斜式不能表示垂直線。

這裡給出的直線的**截距式**

${\frac {x}{a}}+{\frac {y}{b}}=1$    a ≠ 0 且 b ≠ 0

使用了兩個唯一的常數，它們是 x 和 y 截距，但不能用來表示水平線或垂直線，也不能表示穿過 (0,0) 的直線。在本文總結的幾種一般形式中，它的適用性最低。

在最後三種線性函式的一般形式中，斜截式是最有用的，因為它只使用給定直線唯一的常數，並且可以表示任何線性函式。本書以及數學中所有問題都可以不使用點斜式或截距式來解決，除非問題中明確要求使用它們。通常，涉及線性函式的問題可以使用斜截式
(y = m x + b) 和斜率公式來解決。

其他線性方程中的間斷性

設變數 y 依賴於自變數 x 的函式

$y=f(x)\,,$  也即  $y(x)=f\,.$

y 也是函式 f，而 x 也是自變數 ( )。設 y 為表示的商函式

$y={\frac {2x^{2}-5x+3}{x-1}}.$

y 的解的圖形繪製出一組連續的直線點，**除了**x 為 1 的點。用$x=1$ 計算分母會導致除以零，這是一個未定義的條件，不是R 的成員元素，並且在代數閉包之外。y 在點 1,-1 處存在**間斷性**(斷裂) 並且沒有解。在高階研究中，分別處理斷裂點兩側變得非常重要。

y 的其他線性形式可以透過一個**去除**其**間斷性**的方程來表示。從$2x^{2}-5x+3$ 分子中提取因子$x-1$（使用**綜合除法**）。

$y={\frac {2x^{2}-5x+3}{x-1}}.$

$y={\frac {(2x-3)(x-1)}{(x-1)}}.$

$y=2x-3\,,\;x\neq 1$  (對於除 1 之外的所有 x) 。

將它的 (x-1) 個乘法逆元因子（倒數）約簡到乘法單位元（1），保留了$(2x-3)$因子（隱含的通用因子為 1/1）。限制這個簡化函式的定義域；'除了$x=1$之外的所有$x$，其中x未定義'，或者簡單地'且 x ≠ 1'（意味著'且R²'）；使其等同於原函式。此表示式是 x 的線性函式，斜率 m = 2，y 截距縱座標為 -3。表示式$2x-3$在 x = 1 處計算結果為 -1，但在該點函式 y 未定義（除以零）。函式 y 在 x = 1 處存在間斷點。實際上，該函式在該點有一個類似於單點孔（跳躍）的間斷，在圖上顯示為圍繞該點的小空心圓。直線、射線和線段（以及弧、弦和曲線）用虛線或點線表示不連續。

注意：非線性方程也可能是不連續的——參見後續的倒數函式 y = 1/x 的圖形繪製，其中 y 不僅在一個點上，而且在沿 y 軸的“雙”漸近線極值極點上是不連續的。當 x 在更小的幅度（- 和 +）上逼近零時，y 在函式的 - 和 + 對映中均趨於無定義。

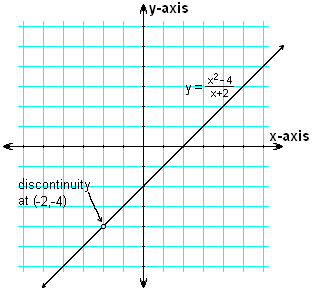
示例：以下函式的圖形是什麼樣子的？

$y={\frac {x^{2}-4}{x+2}}.$

解答

$y={\frac {x^{2}-4}{x+2}}={\frac {(x+2)(x-2)}{(x+2)}}.$

將倒數 (x + 2) 因子約簡到 1。這使得 y = x – 2 對所有 x 都成立，除了 x = -2，在該點存在間斷點。直線 y = x – 2 的斜率 m = 1，y 截距縱座標為 -2。因此，對於最終答案，我們繪製一條斜率為 1、y 截距為 -2 的直線，並在 x = -2 處顯示一個間斷點，否則 y 將等於 -4。
y-intercept ordinate of -2. So for the final answer , we graph a line with a slope of 1 and a y-intercept of -2, and we show a discontinuity at x = -2, where y would otherwise have been equal to -4.

示例：編寫一個函式，其圖形繪製的直線與 y = 2 x – 3 相同，但有兩個間斷點，一個在 x = 0 處，另一個在 x = 1 處。

解答：該函式必須有一個分母，其因子為

分母 = (x – 0)(x – 1) = x (x – 1) 。

在兩個 x 值處具有“零點”。該函式的分子也獲得保留整體因子 1 的因子，表示式相乘

$y={\frac {(2x-3)x(x-1)}{x(x-1)}}={\frac {2x^{3}-5x^{2}+3x}{x^{2}-x}}.$

__________例題結束__________