結合代數/分裂二元數

平面代數

方程 jj=1 表達一個對合，一個在迭代時返回到原點的運算。當 1 被視為單位矩陣時，矩陣方程 mm = 單位矩陣有很多解（即使在 2x2 的情況下），這樣的解就是一個對合矩陣。

分裂二元數利用了這種額外解的概念（超越 1 和負 1）來生成數字集 {x + jy: x,y 在 R 中}。根據

(u+jv)(x+jy) = ux + yv + j(uy + xv)

進行逐分量加法和乘法，這裡稱為分裂二元數的 2-代數，在百科全書中被稱為分裂複數，那裡還提供了一系列同義詞。

為了描述分裂二元數平面的可逆元素，必須從平面中劃去兩條線 x=y 和 y=−x。在這樣形成的四個象限中，包含 1+0j 的一個最為重要，因為任何單位的平方都位於該象限。在其中，集合

G = {exp(aj): a 在 R 中} 形成一個單引數群

exp(aj) exp(bj) = exp((a+b)j).

G ∪ −G 是單位雙曲線 $x^{2}-y^{2}=1\ ,$，但用雙曲函式引數化。

共軛雙曲線是 jG ∪ −jG，也表示為 $\{x+jy:y^{2}-x^{2}=1\}.$

在除法二元數中，垂直和正交是同義詞，但在分裂二元數中，正交在幾何上有所不同，但在代數上是一致的：兩個單位z 和w 是正交的，如果zw* 的實部為 0。雙線性形式表示 <z,w> = 0。例如，對於任何g 在G 中，

g(jg)* = −j gg* = −j exp(aj) exp(−aj) = − j，其實部為零。

練習:

1. 證明單位群U = FxPxG，其中P 是正實數的乘法群，F = {j, −j, 1, −1}，是四元群。
2. 證明x + jy 位於單位所在的象限，當且僅當 y < |x|。
3. 證明乘以 j 的效果是在對角線 x=y 上翻轉平面。
4. 對於g= cosh a + j sinh a，證明當a 增大時，正交點g 和 jg 收斂於漸近線。

同時性

當赫爾曼·閔可夫斯基使用世界線的概念來描述某個物體在時間中的軌跡來開發他的宇宙模型時，他認為運動物體的時間空間取決於其速度。因此，同時性相對於運動的觀察者而言是相對的。分裂二元數中的正交性對應於速度向量與其獨特的時間空間之間的關係。術語雙曲正交性被用來區分它與垂直性。時間空間被稱為時間超平面，因為它是在閔可夫斯基宇宙中的一個三維子空間。

G 的元素可用於在平面上形成群作用。這種作用有時被稱為雙曲旋轉，因為對於任何常數k，雙曲線 {u : u u* = k ≠ 0} 在u -> gu 下是不變集。但是，這種作用不會混合象限，因此術語旋轉並不恰當。另一個效果是，垂直於y=x 的維度被壓縮或擠壓，正如收斂的正交向量g 和 jg 所證明的那樣，其中g = exp(aj) 且a 正在增加。因此，當方向合適時，使用術語壓縮對映。

面積

鑑於 j² = +1，因此當n 為偶數時，jⁿ 為 1，當n 為奇數時，jⁿ 等於 j。因此

$\exp(aj)\ =\ \cosh a+j\sinh a$ 因為 j 的冪將偶數項和奇數項分開。

變數a 是沿著單位雙曲線 $x^{2}-y^{2}=1.$ 的雙曲角。這種配置是自然雙曲線的標準化形式，其中現在乘法單位距離原點一個單位距離，因此扇區面積是角度大小的一半，因為標準化。

在 D 中，乘法進行壓縮，而不是壓縮對映保留自然雙曲線的扇區面積。狹義相對論中速度加法的重新線性化使用了 D 中單位雙曲線的引數化。實際上，如果兩個快度a 和b 相加，結果將根據$e^{aj}\ e^{bj}=e^{(a+b)j}$ 在 D 中相加。

D 中的正交性概念在算術上與 C 中的條件一致，但表示的是雙曲正交性，即世界線與其時間超平面的關係。儘管只有二維，但分裂二元數有助於理解狹義相對論。

練習

單位雙曲線 右支在 D 上的群作用對應於 R² 上的壓縮對映 σ。

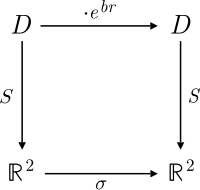
1. 矩陣 $S={\begin{pmatrix}1&1\\1&-1\end{pmatrix}}$ 且 σ 是 R² 上的壓縮對映。證明矩陣S 提供了一個對映，使得 D 和 (R², xy) 作為環和二次空間同構，但S 不是歐幾里得度量的實平面上的等距。

2. 對於K ⊂ D，area(K) 有限，以及 R 中的任何a 且u = exp(aj)，證明 {u k : k 在 K 中} 的面積等於K 的面積。

3. 雙曲角與調和級數$\sum _{n=1}^{\infty }1/n\ ?$  有什麼共同之處？答案：無界。比較它們的幾何形狀。

4. 繪製子群$\{pj^{n}e^{aj}:p>0,\ n=0,1,\ a\in R\}\subset U.$