核醫學基礎物理/核醫學動力學研究

引言

這是華夏公益教科書中名為 核醫學基礎物理 的一個正在開發的章節。

人體中物質的 代謝 是許多相互關聯的動態過程的結果，包括物質的吸收、分佈、利用、降解和排洩。僅測量其中一個引數可能會得到一個表明疾病的結果，但可能無法確定疾病的實際原因。當獲得完整代謝系統的知識時，可能會確定有關原因的更詳細資訊。獲得這種知識的一種方法是透過對生理系統的數學模擬。這種方法的結果包括生成整個系統的表示以及對系統組成部分之間相互作用的理解。這種方法通常涉及

1. 在透過新增合適的示蹤劑刺激系統後獲取實驗資料；
2. 將實驗資料與數學模擬預測的資料進行比較；以及
3. 使用諸如 最小二乘法、最大似然法 和 蒙特卡羅模擬 等方法，改變模擬引數，直到兩組資料儘可能地一致。

這種方法的一般假設是

• 示蹤劑的新增不會擾亂系統；
• 被追蹤物（即正在研究的物質）在整個過程中是守恆的；
• 示蹤劑在整個過程中是守恆的——允許放射性衰變；以及
• 系統處於穩態（即系統每個隔室中被追蹤物的量保持恆定，每個隔室之間被追蹤物的交換也保持恆定）。

目前使用兩種主要型別的數學模型

• • 確定性：其中使用解析表示式來描述示蹤劑在系統每個部分隨時間的精確行為。使用的數學表示式通常是指數函式或冪函式；

• • 隨機：其中系統的行為由隨機過程決定，隨機過程由機率函式描述。

下面將詳細討論確定性模型。

隔室分析

這種形式的確定性分析涉及將生理系統劃分為多個相互連線的隔室——其中隔室定義為系統的任何解剖、生理、化學或物理細分。一個基本假設是示蹤劑在整個隔室中均勻分佈。最簡單的系統是單隔室模型。我們將從這個簡單的模型開始處理，然後擴充套件到更復雜的模型——最初的模型僅是為了開發框架，而後的模型則與核醫學動力學研究直接相關；它們的獲取和分析。

有一個名為 Compartments_TP 的 ImageJ 外掛可用，它提供了對許多其他模型的模擬。

單隔室模型

示蹤劑透過血管的流動，在理想的脈衝注射後，在下圖中顯示為單隔室模型的示例。圖中所示的隔室是封閉的，除了被追蹤物的流入和流出，示蹤劑如箭頭所示注入。在這些理論條件下，示蹤劑將在注射後立即並在整個隔室中均勻混合。其數量將隨著時間的推移而減少，這取決於流出的速率。圖中使用的變數是

q：時間t時隔室中示蹤劑的數量；以及
F：流出。

單隔室模型

我們可以將週轉率k定義為這兩個引數的比率，即

$k={\frac {-dq/dt}{q}}$

可以改寫為

${\frac {dq}{dt}}=-kq$

無需詳細介紹數學細節（與 放射性衰變定律 的推導類似！），該方程的解是

$q=q_{0}\ exp(-kt)\,\!$

其中q_o是時間t = 0時存在的示蹤劑數量。

下圖繪製了該方程，以說明週轉率k的值的影響。

示蹤劑數量 q 相對於時間的圖形說明，對於週轉率 k 的相對高低值。

<

該圖表明，在注射後，隔室中的示蹤劑數量將隨時間呈指數下降，下降速率取決於流出，這可能符合直覺預期。

雙隔室模型 - 閉合系統

一套更復雜，但仍然相對簡單的模型是基於兩個隔室的模型。在閉合系統中，示蹤劑只是在兩個隔室之間移動，而不會有任何整體損失或增益——見下圖

閉合雙隔室模型

因此，

${\frac {dq_{1}}{dt}}=k_{21}q_{2}-k_{12}q_{1}$

以及

${\frac {dq_{2}}{dt}}=k_{12}q_{1}-k_{21}q_{2}$.

由於系統中沒有示蹤劑損失，

$q_{1}+q_{2}={\text{constant}}=q_{0}\,\!$

因此，

${\frac {dq_{1}}{dt}}=-{\frac {dq_{2}}{dt}}\,,$

表明，當隔室#1中示蹤劑數量減少時，隔室#2中的數量增加，反之亦然。現在，考慮上圖所示的情況，示蹤劑在時間 *t* = 0 時注入隔室#1。此時，

$q_{1}=q_{0}\,\!$

以及

$q_{2}=0\,,\,\!$

以及，最初，

${\frac {dq_{1}}{dt}}=-k_{12}q_{0}$

以及

${\frac {dq_{2}}{dt}}=k_{12}q_{0}$

這些方程的解是

$q_{1}=q_{0}\left\lbrack 1-{\frac {k_{12}}{k_{12}+k_{21}}}\left\lbrace 1-\ {\text{exp}}\ -(k_{12}+k_{21})t\right\rbrace \right\rbrack$

以及

$q_{2}=q_{0}\left\lbrack {\frac {k_{12}}{k_{12}+k_{21}}}\left\lbrace 1-\ {\text{exp}}\ -(k_{12}+k_{21})t\right\rbrace \right\rbrack$

它們在特殊情況下 *k*₁₂ = *k*₂₁ 且兩個隔室體積相同時的行為，如下所示

隔室#1 和 #2 中示蹤劑數量隨時間變化的圖形說明。

請注意，該模型預測，當隔室#1 中示蹤劑數量呈指數下降，隔室#2 中示蹤劑數量呈指數上升時，將達到穩態，每個變化的速率由週轉率之和控制。

雙隔室模型 - 開放鏈式系統

這是前面提到的單隔室模型的擴充套件，它包含兩個串聯的隔室，如下圖所示

開放鏈式雙隔室模型。

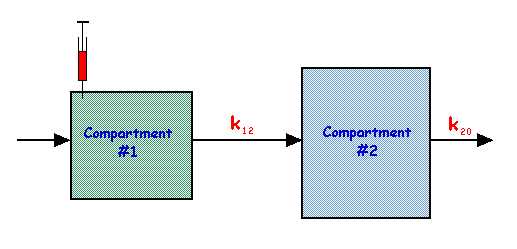
在這個模型中，

${\frac {dq_{1}}{dt}}=-k_{12}q_{1}$

以及

${\frac {dq_{2}}{dt}}=k_{12}q_{1}-k_{20}q_{2}$

這些方程的解是

$q_{1}=q_{0}\ {\text{exp}}(-k_{12}t)$

以及

$q_{2}=q_{0}{\frac {k_{12}}{k_{12}-k_{20}}}\lbrack {\text{exp}}(-k_{20}t)-{\text{exp}}(-k_{12}t)\rbrack \,,$

並且當 k₂₀ 為 k₁₂ 的三倍時，q₁ 和 q₂ 的行為如下圖所示

開放式串聯雙室模型中示蹤劑量隨時間的變化圖。

請注意，此圖中 q₂ 的行為類似於靜脈注射後動脈示蹤劑的流動，以及放射劑量學中使用的 累積活度 引數。

雙室模型 - 開放式乳頭系統

該模型等同於上面討論的封閉式雙室系統，但在其中增加了一個從一個室流出的路徑。

開放式乳頭雙室模型。

在這種情況下，

${\frac {dq_{1}}{dt}}=-k_{10}q_{1}-k_{12}q_{1}+k_{21}q_{2}$

以及

${\frac {dq_{2}}{dt}}=k_{12}q_{1}-k_{21}q_{2}$

當 t = 0 時

$q_{1}=q_{0}\,\!$

以及

$q_{2}=0\,\!$

最初，

${\frac {dq_{1}}{dt}}=-(k_{10}+k_{12})q_{1}$

以及

${\frac {dq_{2}}{dt}}=k_{12}q_{0}$

這些方程的解是

$q_{1}=q_{0}\left\lbrack {\frac {k_{21}-a_{1}}{a_{2}-a_{1}}}{\text{exp}}(-a_{1}t)+{\frac {k_{21}-a_{2}}{a_{1}-a_{2}}}{\text{exp}}(-a_{2}t)\right\rbrack$

以及

$q_{2}={\frac {q_{0}k_{12}}{a_{2}-a_{1}}}\lbrack {\text{exp}}(-a_{1}t)-{\text{exp}}(-a_{2}t)\rbrack$

其中

$a_{1}a_{2}=k_{10}k_{21}\,\!$

以及

$a_{1}+a_{2}=k_{10}+k_{21}+k_{12}\,\!$

q₁ 和 q₂ 的行為在下面的圖中說明。

開放性乳頭狀雙室模型中示蹤劑數量與時間的圖形說明。

該模型已被廣泛應用於

• 血漿蛋白 代謝的研究，其中 1 號室代表血漿，2 號室代表血管外空間。
• 鎝離子在甲狀腺 中的捕獲，其中
  • 1 號室：血漿。
  • 2 號室：甲狀腺。
  • k₁₂：從血漿到腺體的清除率。
  • k₂₁：從腺體到血漿的洩漏率。

三室模型

上面的開放性乳頭狀模型已被擴充套件到使用第三室來研究碘攝取，該室由從 2 號室的不可逆流k₂₃供給。

甲狀腺碘攝取模型。

其中

• 1 號室：血漿。
• 2 號室：甲狀腺中無機碘的捕獲。
• 3 號室：甲狀腺內已與激素合成過程中的有機成分結合的碘。

開放性乳頭狀模型也被應用於腎臟清除率，其中系統由一個血管內室組成，一個血管外室與其交換並與尿液室不可逆地連線。

腎臟清除率模型。

上圖中的血管內室（#1）代表可與腎實質和血管外空間交換的示蹤劑。尿液室（#2）代表已被腎臟清除的示蹤劑，因此與腎盂和膀胱相關。血管外室（#3）代表未被清除的示蹤劑，例如與其他分子結合的示蹤劑或腎外組織中的示蹤劑。

當示蹤劑透過周圍靜脈注入血管內室時，初始分佈不會在全身均勻分佈 - 但隨著血液迴圈，這種非均勻性會逐漸消失。對於高度血管化的區域，示蹤劑數量與時間的曲線將顯示出初始的急劇上升，然後迅速下降。此峰值的幅度將隨以下因素而變化：

• 解剖區域。
• 注射部位。
• 注射速度。

因此，隔室分析不能應用於腎圖的這一階段，因為隔室分析中隱含的示蹤劑均勻分佈的基本假設不適用。

在此階段之後，由於以下原因，血管內室中的示蹤劑數量開始下降：

• 被腎臟吸收 - 上圖中的k₁₂表示。
• 擴散到血管外空間 - 上圖中的k₁₃表示。

隨著血管外室中示蹤劑數量的增加，反方向的交換開始發生（上圖中的k₃₁表示），因此在示蹤劑數量下降之前會達到最大值。以下圖說明了當

k12 = 0.05 每分鐘	k13 = 0.04 每分鐘	k31 = 0.06 每分鐘
l1 = 0.13 每分鐘	l2 = 0.024 每分鐘
A1 = 0.65	A2 = 0.35

腎臟清除率模型的預測。

最終，所有示蹤劑都將最終進入尿液室。

上面圖中使用的方程為

$q_{1}=A_{1}\ {\text{exp}}(-l_{1}t)+A_{2}\ {\text{exp}}(-l_{2}t)\,\!$

$q_{2}=A_{3}\ {\text{exp}}(-l_{1}t)-A_{4}\ {\text{exp}}(-l_{2}t)\,\!$

$q_{3}=A_{5}\ \lbrack {\text{exp}}(-l_{1}t)-A_{2}\ {\text{exp}}(-l_{2}t)\rbrack \,\!$

其中l₁ 和 l₂ 是與分數週轉率相關的常數，A₁ 到 A₅ 也是常數，使得

$A_{1}+A_{2}=1\,\!$

以及

$A_{3}+A_{4}=1\,\!$

在實踐中，腎清除率可以透過監測血管內區室中示蹤劑的量來獲得，例如血漿濃度P，其中

$P={\frac {\text{Quantity of Tracer in Intravascular Space}}{\text{Volume of Intravascular Space}}}$

這種血漿濃度的時間依賴性將與q₁的變化方式相同，因此

$P(t)=C_{1}\ {\text{exp}}(-l_{1}t)+C_{2}\ {\text{exp}}(l_{2}t)\,\!$

其中C₁和C₂分別與A₁和A₂相關。因此，腎清除率與k₁₂相關，可以透過表徵血管內區室中示蹤劑量的雙指數衰減來確定。

腎小球濾過率

腎小球濾過率（GFR）通常被認為是腎功能最重要的單一指標之一。它在評估腎衰竭的存在和嚴重程度方面尤為重要。

有三種主要方法可以確定患者的 GFR

• 菊粉清除率，
• 肌酐清除率，
• 放射性示蹤劑清除率。

菊粉清除率已使用多年，通常被認為是三種方法中最可靠和最準確的方法。然而，其主要缺點包括需要持續靜脈輸注、透過膀胱導管進行定時尿液收集以及漫長的化學分析。肌酐清除率因此已被廣泛用於常規 GFR 評估。然而，雖然這種方法在正常情況下與菊粉清除率產生類似的結果，但在中度至晚期腎衰竭患者中其結果的有效性值得懷疑，因為腎小管分泌的意義越來越大。

第三種方法，放射性示蹤劑清除率已被廣泛採用，使用⁵¹Cr-EDTA。這種示蹤劑已知在生理上是惰性的，不與血漿蛋白結合，也不被紅細胞或腎臟以外的器官代謝。它通常在注射後 24 小時內排洩，其中 98% 透過腎臟排洩。⁵¹Cr 的半衰期約為 28 天，並透過 100% 的電子俘獲衰變為穩定的釩，在大約 10% 的轉化中發射單能（320 keV）伽馬射線。此外，⁵¹Cr-EDTA 測定的 GFR 可與 OIH 腎血漿流量評估結合使用，用於各種腎臟疾病的鑑別診斷。

⁵¹Cr-EDTA 清除率通常使用的放射性活度為 1-10 MBq，放射性藥物通常透過靜脈注射給藥。這種單次注射技術透過靜脈血樣評估 GFR，在最簡單的情況下，或者透過更復雜的方法連續外部監測⁵¹Cr 中的伽馬射線。當患者計數與時間在對數/線性軸上作圖時，會生成一條曲線，它最初迅速下降，然後以恆定速率下降，代表q₁在我們最後一張圖中的行為。這種初始下降是由於放射性示蹤劑與血管外、細胞外液之間的平衡建立所致。較慢的第二階段反映了腎臟排洩，幷包含評估 GFR 所需的資訊。

⁵¹Cr-EDTA 的血漿清除率是使用上面討論的三室模型預測的。

一種快速簡便的技術是從患者身上獲取兩個血樣，一個在注射後兩小時，另一個在注射後四小時。使用閃爍計數器確定每個樣品中血漿中每單位體積的計數，並與標準溶液中的計數進行比較。標準溶液是透過將與患者相同的注射液稀釋在已知體積的水中製成的，例如 1 升。

上述曲線第二部分的斜率 m 可以由以下公式確定

$m={\frac {\ln b_{1}-\ln b_{2}}{t_{2}-t_{1}}}$

其中

• t₁：第一個血樣注射後的時間，通常為 120 分鐘，
• b₁：第一個血樣血漿中的計數/毫升（mL）（已校正背景計數），
• t₂：第二個血樣注射後的時間，通常為 240 分鐘，
• b₂：第二個血樣血漿中的計數/mL（也已校正背景）。

現在，我們可以將這條直線外推到注射時間t₀，以確定示蹤劑在患者血漿區室中瞬時混合時的血漿計數，即

$\ln b_{0}=\ln b_{1}+m(t_{1}-t_{0})\,\!$

如下圖所示

兩個血漿樣品的計數擬合到一條直線，這條直線外推到注射時間（虛線），以確定 b₀ 的對數。使用三室模型預測的血漿清除率 q₁ 以陰影顯示。

因此，我們可以寫

$b_{0}={\text{exp}}\ {\big (}\ln b_{1}+m(t_{1}-t_{0}){\big )}$

現在可以使用**稀釋原理**透過比較血漿計數和標準溶液的計數來確定該血漿隔室的體積，即

$V={\frac {S\cdot V_{s}}{b_{0}}}$

這導致

$V={\frac {S\cdot 1000}{b_{0}}}$

當標準注射稀釋在 1 升中時。然後用以下公式給出清除率（以毫升/分鐘表示）

${\text{Clearance}}=V\cdot m\,\!$

下面顯示了兩個患者的結果，以說明此技術。

患者 A

樣本	計數/毫升
背景	477
b1 在 119 分鐘	11,438
b2 在 238 分鐘	6,235
標準，S	150,020

該患者的⁵¹Cr-EDTA 清除率被確定為 38.8 毫升/分鐘。評估結果表明慢性腎功能衰竭，後來發現是由於狼瘡性腎炎引起的。隨後患者接受了類固醇治療。

兩個月後，患者再次接受檢測，發現清除率升至 52.7 毫升/分鐘。對於患者的年齡，該清除率被認為在正常範圍內，表明治療正在產生積極效果。然後停止治療。兩個月後，患者再次接受檢測，在此期間未接受類固醇治療。結果為 54.2 毫升/分鐘，反映出治療成功。

患者 B

樣本	計數/毫升
背景	425
b1 在 122 分鐘	3,103
b2 在 250 分鐘	1,390
標準，S	104,600

該患者血壓高，需要確認腎臟受累情況。然而，清除率為 117.3 毫升/分鐘，遠在正常範圍內。因此，排除了腎臟對該患者疾病的調查。

---

請注意，血液樣本數量不限於兩個，有些方法需要三個、四個或更多樣本，而其他方法使用外部監測清除率。然而，每種方法都基於上述分析形式，其中確定清除曲線第二階段的速率常數以及放射性示蹤劑的分佈體積。因此，血液取樣時間是在第一階段結束後，即注射後超過約兩個小時，使用單指數擬合到此後階段來確定分佈體積。

---

重要的是要理解，如上所述確定的⁵¹Cr-EDTA 清除率並不直接等同於腎小球濾過率 (GFR)，因為該方法假設單指數依賴性。因此，⁵¹Cr-EDTA 清除率結果通常透過經驗或理論推導的因子進行校正，以迫使它們表示真實的 GFR。經驗校正包括

• Chantler (1969)，其中⁵¹Cr-EDTA 清除率乘以 0.8 的因子；
• Brien (1969)，其中大於 50 毫升/分鐘的清除率乘以 0.82 並加上 6；
• Brochner-Mortensen (1972)，其中應用二階多項式

獲得 GFR。基於隔室分析的真實 GFR 與單指數清除率值之間關係的理論考慮的校正已引入(Fleming, 2007)，它提供了改進的校正，特別是在高 GFR 時。此校正的形式為

$GFR={\frac {\text{Clearance}}{(1+f\cdot {\text{Clearance}})}}$

其中 $f$ = 0.0017 分鐘/毫升。

作為最後一步，校正後的清除率測量通常標準化為標準人的體表面積 (BSA)，即 1.73 平方米。這通常是使用基於患者身高和體重的 BSA 估計值來完成的 - 例如，來自DuBois (1916)或Haycock (1978)。還引入了基於 BSA 縮放清除率的單指數校正技術 (Jodal & Brochner-Mortensen, 2008)，它類似於 Fleming (2007) 的方法，但在兒科研究中提供了改進的校正。

腎圖

從上面的討論中應該清楚，尿液隔室（＃2）包含尿液中示蹤劑的數量，而不區分尿液是在腎盂、輸尿管還是膀胱中。可以透過將三隔室乳頭模型擴充套件到五個隔室來合併這些解剖空間

應用於腎圖的隔室分析。

請注意，示蹤劑透過腎實質的透過可以用轉運時間t₀來表徵，並且k₅₆與尿液生成率相關。

腎實質、腎盂和膀胱中示蹤劑數量的最終微分方程的解包含對時間延遲t₀的考慮，因此

• 當t < t₀

${\color {Blue}q_{4}=1-A_{3}\ {\text{exp}}(-l_{1}t)-A_{4}\ {\text{exp}}(-l_{2}t)}\,\!$

${\color {Red}q_{5}=0}\,\!$

${\color {OliveGreen}q_{6}=0}\,\!$

• 當 t > t₀

${\color {Blue}q_{4}=A_{3}[1-{\text{exp}}(-l_{1}t_{0})]{\text{exp}}(-l_{1}\lbrace t-t_{0}\rbrace )+A_{4}[1-{\text{exp}}(-l_{2}t_{0})]{\text{exp}}(-l_{2}\lbrace t-t_{0}\rbrace )}\,\!$

${\color {Red}q_{5}=A_{7}\ {\text{exp}}(-l_{1}\lbrace t-t_{0}\rbrace )+A_{8}\ {\text{exp}}(-l_{2}\lbrace t-t_{0}\rbrace )-A_{9}\ {\text{exp}}(-l_{3}\lbrace t-t_{0}\rbrace )}\,\!$

${\color {OliveGreen}q_{6}=1-A_{10}\ {\text{exp}}(-l_{1}\lbrace t-t_{0}\rbrace )-A_{11}\ {\text{exp}}(-l_{2}\lbrace t-t_{0}\rbrace )+A_{12}\ {\text{exp}}(-l_{3}\lbrace t-t_{0}\rbrace )}\,\!$

其中 l₃ 與 k₅₆ 相關。每個隔室中示蹤劑數量的時間過程如下圖所示

使用 t₀ = 2 分鐘和 k₅₆ = 1 每分鐘生成的腎實質 (q₄)、腎盂 (q₅) 和膀胱 (q₆) 曲線。

可以透過將腎實質和腎盂曲線相加來獲得整個腎臟中示蹤劑的數量，因此

$q_{\text{kidney}}=q_{4}+q_{5}\,\!$

如下圖所示

腎盂和實質曲線相加的結果。

在實踐中，腎圖記錄的不僅僅是腎臟曲線，還有示蹤劑在

• 重疊和底層組織，以及
• 腎臟本身的血管內空間。

這些貢獻疊加了真實的腎圖，形成了一個 **背景**。背景中示蹤劑的數量隨時間變化，但與真實的腎臟曲線變化方式不同。該背景的時間過程可能與前面使用五隔室模型得出的血管內 (q₁) 和血管外 (q₃) 曲線的總和類似。

在此基礎上，可以推匯出以下公式

$q_{\text{Bgd}}=b_{1}q_{1}+b_{3}q_{3}\,\!$

其中 b₁ 和 b₃ 分別代表血管內和血管外空間中示蹤劑對檢測到的腎圖曲線的貢獻。例如，下面的曲線使用 b₁ = 0.05 和 b₃ = 0.02 生成，以及

$q_{\text{Renogram}}=0.5\,q_{\text{Kidney}}+q_{\text{Bgd}}\,\!$

實際中獲得的腎圖和背景曲線典型示例。

實際上，應該從原始腎圖資料中減去此背景曲線，以獲得反映腎臟中示蹤劑真實量的曲線（見前圖）。此過程有時被稱為 **血液背景扣除**——雖然你現在應該能夠理解，這是一個有點錯誤的說法！

下面顯示了未校正和校正後的曲線，以幫助直接比較。

腎圖曲線在背景校正前後。

以及患者 ^99mTc-DTPA 腎圖的示例，如下所示，以幫助您將其與室模型分析的預測結果進行比較。

最後一張圖說明了一種可用於 ^99mTc-MAG3 腎圖的分析方法，適用於患有梗阻性泌尿道病的患者。

MAG3 腎圖分析。

腎圖中的背景扣除

在實踐中，在解釋腎圖時必須考慮腎圖中的背景活性。這通常透過估計背景活性並將其從原始腎圖資料中減去來實現。問題是：如何測量這種背景活性？

一種方法是基於記錄患者腎切除部位的活性，這些患者的剩餘腎臟正在接受檢查。但是，應該注意的是，切除腎臟也會去除背景活性的血管內來源。因此，腎切除部位在腎圖影像中通常比腎外組織更冷。

一種潛在的更好方法是記錄非功能性腎臟區域的活性。

然而，在大多數患者中，必須使用非腎臟區域來估計背景。理想情況下，區域的選擇應該反映與腎臟本身相同的血管內和血管外背景。在這個領域似乎沒有標準化，實踐包括使用腎臟之間的區域、腎臟上方、心臟上方以及每個腎臟下方。

Taylor 等人 (1997) 提供了此類方法的比較，並且類似但更基本分析的結果總結如下。

Bgd RoI 位置

這些腎圖影像使用蒙特卡洛模擬 生成，並使用 OsiriX 分析。分裂函式使用 90-150 秒時間段內的計數積分計算。平均絕對百分比誤差是從一系列此類模擬影像中計算得出的，其中左腎與右腎的分裂函式從 100%:0% 到 50%:50% 再到 0%:100%，步長為 5%。

可以看出，側向 RoI 產生的百分比誤差最低，而中心 RoI（在早期使用 ^99mTc-DTPA 進行伽馬相機腎圖時使用）產生的誤差明顯更大，約為 12%。這與目前的臨床實踐一致，在目前的臨床實踐中，不再使用中心 RoI，而更傾向於使用側向或傾斜的 RoI，或腎周 RoI。

相比之下，沒有背景校正會產生 20.7% 的誤差，這突出了背景校正的整體重要性。

對於真實的 LK:RK 分裂函式比率 50%:50% 以及 100%:0% 和 0%:100% 的極值，背景活性的變化如下圖所示。

側向背景資料的 6 次多項式擬合。

使用 32 幀平均值在時間上平滑的蒙特卡洛模擬 AP 腎圖。原始資料由 dynamicrenalstudy.org 提供。

首先要注意的是，背景曲線隨時間的變化方式反映了腎臟曲線本身，在攝取階段迅速上升，在排洩階段緩慢下降。其次，請注意，右腎 (RK) 曲線下降速度比左腎 (LK) 曲線慢——這可能是由於 MAG3 示蹤劑在肝臟中滯留造成的。這與 之前 分析模型中使用的假設完全不同。從左側的蒙特卡洛模擬 AP 腎圖 可以看出肝臟參與的程度，其中可以觀察到整個研究過程中肝臟及其動態的合理檢視。這與用於生成虛擬研究的藥代動力學模型 一致。

第三，請注意，在 50%:50% 和 0%:100% 時，RK 曲線比 LK 曲線幅度更大，而在 100%:0% 時則相反。這突出了需要對每個腎臟使用單獨的背景 RoI。

最後一點需要注意的是，與 90-150 秒的時間視窗有關，在該視窗中通常應用 積分或斜率方法。可以看出，背景計數的總和（**積分**）和這些計數的變化率（**斜率**）在此期間都在變化，這表明這兩種方法都會受到背景曲線這些特徵的影響。

選擇好背景區域並生成活性/時間曲線後，應該將背景曲線按一個取決於背景區域和腎臟區域的相對面積的因子進行縮放，然後將其從原始腎圖曲線中減去。此外，請注意，一些實踐還包括根據腎臟位置進一步縮放背景曲線。最後，開發了更復雜的方法來進行背景校正，包括

• 根據腎臟周圍的背景樣本生成插值背景區域，
• 使用外推技術估計背景校正因子，以及
• 反捲積分析。.

需要注意的是，在將這些結果直接轉化為真實患者研究時應謹慎，因為原始資料來自室模型的二維表示。

相對腎功能

患者腎臟的相對功能通常定義為該腎臟的腎臟清除率，以患者總腎臟清除率的百分比表示，即

${\text{LK Relative Fn.}}={\frac {\text{LK Clearance}}{{\text{LK}}+{\text{RK Clearance}}}}$

以及

${\text{RK Relative Fn.}}={\frac {\text{RK Clearance}}{{\text{LK}}+{\text{RK Clearance}}}}$

其中 LK 和 RK 分別代表左腎和右腎。

假設

• N_Kidney(t)：背景校正後的腎臟計數率，以及

• N_Bgd(t)：來自血管內感興趣區域的計數率。

此時應該很明顯

$N_{\text{Kidney}}(t)\ \alpha \ q_{4}(t)\,\!$

以及

$N_{\text{Bgd}}\ \alpha \ q_{1}(t)\,\!$

因此，我們可以得出結論，在腎圖的初始階段，即當 t < t₀ 時

$N_{\text{Kidney}}(t)=UC\int _{0}^{t}N_{\text{Bgd}}(t)\cdot dt$

其中 UC 是腎臟攝取常數。此常數與該腎臟的清除率相關，因此我們可以寫成

${\text{LK Relative Fn.}}={\frac {\text{LK Update Constant}}{{\text{LK}}+{\text{RK Uptake Constant}}}}$

以及

${\text{RK Relative Fn.}}={\frac {\text{RK Uptake Constant}}{{\text{LK}}+{\text{RK Uptake Constant}}}}$

然而，我們已經從上面看到背景校正後的腎臟計數率與攝取常數直接相關，因此我們可以得出結論

${\text{LK Relative Fn.}}={\frac {\text{LK Counts}}{{\text{LK}}+{\text{RK Counts}}}}$

以及

${\text{RK Relative Fn.}}={\frac {\text{RK Counts}}{{\text{LK}}+{\text{RK Counts}}}}$

請注意，此分析表明，可以透過測量初始血管峰值後但在排洩階段開始之前每個腎臟中的相對計數來確定相對腎臟功能。

腎臟深度校正

鑑於兩個腎臟可以在患者體內處於不同的深度，通常會對光子衰減的差異進行校正。傳統的方法是在進行腎圖後獲取側檢視，以測量每個腎臟的深度，並基於假定的伽馬射線能量線性衰減係數（例如，^99mTc 伽馬射線為 0.153 cm^-1）進行指數校正。

以下研究說明了這種情況，其中右腎比左腎深約 1 釐米。該研究實際上是通過蒙特卡羅模擬數字體模 (XCAT) 生成的影像，其中包括光子衰減、散射、有限空間解析度和噪聲的影響。左腎的位置深度為 7.31 釐米，而右腎的深度為 8.64 釐米，分割功能為 50:50。

[[File:nm14 301e.gif|thumb|center|A virtual renogram acquired at 10 seconds per frame for 120 frames. Raw data courtesy of dynamicrenalstudy.org|alt=A virtual renogram.

用於腎圖分析的感興趣區域。

請注意，由於衰減的差異，兩條曲線並沒有重疊，而這在 50:50 分割功能中是預期的。透過 90 到 150 秒之間的計數積分估計的分割功能為 54:46。然而，當校正這種衰減差異時，將獲得以下曲線，並且分割功能估計現在更接近實際的 49:51。

虛擬腎圖，衰減校正。

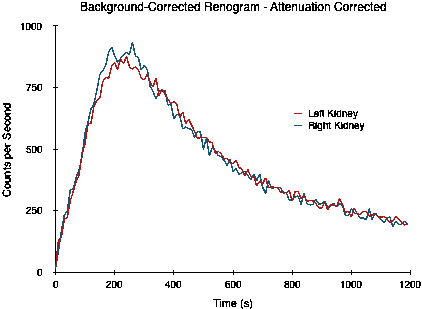
商業腎臟分析軟體通常提供基於患者身高和體重與每個腎臟深度之間經驗得出的關係自動計算腎臟深度的選項。其中一個軟體包提供了以下選項（體重以公斤表示，身高以釐米表示）

方法	左腎深度 (cm)	右腎深度 (cm)
標準	13.2*(體重/身高)+0.7	13.3*(體重/身高)+0.7
埃默裡	16.17*(體重/身高)+0.027*年齡（年） - 0.94	15.13*(體重/身高)+0.022*年齡（年） + 0.077 注意：包含印刷錯誤
伊藤	14.0285*(體重/身高)0.7554	13.6361*(體重/身高)0.6996
T. 伊藤	17.05*(體重/身高) + 0.13	16.55*(體重/身高) + 0.66

下圖顯示了這些方程在廣泛的體重身高比範圍內生成的腎臟深度差異的圖形表示（注意：埃默裡公式假定了 50 歲的年齡）

腎臟深度差異（左腎深度減去右腎深度）。

可以看出，標準公式預測的深度變化很小，因此派生的衰減校正可能對相對功能估計的影響很小。還可以看出，T. 伊藤公式表明右腎始終比左腎更深。後兩組公式表明，對於體重身高比小於 0.6 到 0.7 的情況，右腎更深，而在該範圍之上，左腎更深。可以看出，這後三組公式預測的總體深度差異範圍不超過 ±5 毫米。這種差異產生的預期衰減校正因子在 0.95 到 1.05 的範圍內。

應將這些公式的預測與腎臟深度研究的結果進行對比，研究結果表明，在約 60% 的患者中可以預期大於 5 毫米的差異，而在約三分之一的患者中可以預期大於 1 釐米的差異。因此可以推斷，上述公式僅在不到一半的患者中提供足夠的衰減校正，並且偶爾可以預期衰減校正因子低至 0.6。

因此，顯而易見的是，準確的腎臟深度測量對於正確解釋所有腎圖至關重要，並且應謹慎使用自動腎臟深度公式。

^99mTc-MAG3 腎圖分析的半自動方法

腎圖分析的商業軟體通常提供多種所謂的半自動分析方法——其中一些分析功能需要使用者互動（例如腎臟識別），而其他功能則自動執行（例如計算），以確定腎臟分割功能和有效腎血漿流量 (ERPF)。在此，軟體可能會要求使用者例如

• 輸入患者的身高和體重——以便使用經驗得出的公式計算體表面積和腎臟深度，以及
• 在每個腎臟周圍定義感興趣區域 (RoI)——並自動在這些腎臟 RoI 旁邊放置背景區域。

為這四個 RoI 生成計數/時間曲線。然後自動將背景 RoI 中的計數按比例縮放到與相應腎臟 RoI 大小相同的背景區域的計數，並將縮放後的背景曲線從腎臟曲線中減去，以生成每個腎臟的淨腎圖曲線。

然後使用每個腎圖中預定義時間間隔內（例如注射後 1 到 2 分鐘）的計數來計算

• 計數的總和（稱為積分）和/或
• 計數的增加速率（稱為斜率）

每個腎臟。

使用前面使用的腎圖系列的側向 RoI 進行背景減法，並使用 90 到 150 秒的時間段進行分析，對這兩種方法進行了比較。兩種方法都產生了非常相似的結果

然而，積分方法產生的平均絕對百分比誤差僅為 2.6%，而斜率方法產生的誤差明顯更大，為 9.4%——主要原因是 LK/RK 比率較低和較高時的精度不足。

相比之下，使用積分法時，沒有進行背景校正會導致 20.7% 的誤差，而使用斜率法時，誤差僅為 9.2%。這再次強調了此類校正的重要性。

可以使用每個腎臟的計算深度和假定的^99mTc伽馬射線的線性衰減係數來校正積分以消除組織衰減。以這種方式計算積分是這種分析方法的主要誤差來源，因為使用患者的身高和體重（以及某些方法中的年齡）來確定腎臟深度可能會不準確 - 請參閱上一節。此外，腎臟顯像掃描情況下的線性衰減係數 (μ) 值沒有標準，臨床使用值如 0.12、0.14 和 0.153 每釐米。例如，對於 6 釐米的腎臟深度，這些 μ 值會導致應用 2 到 2.5 之間的校正因子，即給出約 20% 的變化。

分割函式可以透過每個腎臟的衰減校正 (AC) 積分對兩個腎臟的 AC 積分之和的百分比貢獻來確定。

此外，腎臟攝取可以透過將 AC 積分表示為注射劑量的百分比來確定。

有效腎臟血漿流量 (ERPF) 然後可以根據經驗推導的公式計算，例如

左腎 ERPF (毫升/分鐘) = -21.579 + (11.621 * 左腎攝取)

以及

ERPF 值 (毫升/分鐘) = 14.98 * (左腎攝取 + 右腎攝取) + 8.28

或者，可以將洗脫係數定義為

0.48026*(exp(1.35315*腎臟攝取總和)/100)-1

乘以血漿體積估計值，例如

體表面積 * 1,000 + 0.608 毫升

得到總 MAG3 清除率。此最終因子用於使用以下公式計算總 ERPF (毫升/分鐘)

1.25821* (總 MAG3 清除率) + 18.34451

0.53 也被用作 ERPF 轉換因子，即從 ERPF 轉換為 MAG3 清除率。但是，需要注意的是，該因子的值在 0.61 到 0.9 之間。

作為這些基於積分的方法的替代方案，腎臟曲線在腎臟顯像的攝取階段的斜率已被用來定義每個腎臟的斜率指數，該指數基於每個腎臟顯像的斜率，針對腎臟深度進行衰減校正，並表示為注射劑量的百分比乘以 10⁶! 然後可以推測透過將每個腎臟的斜率指數與斜率指數之和相關聯來獲得分割函式 - 並使用以下公式計算總 MAG3 清除率

(12.725 * 腎臟斜率指數之和 + 6.24)/體表面積

體表面積 (BSA) 估算也是這些計算中變化的另一個來源。它被廣泛用於將患者的 ERPF 參考到標準 BSA，例如 1.73 平方米。它也用於使用上述公式等公式進行計算。該領域至少使用兩種 BSA 計算方法，如下所述

Du Bois 公式：BSA = 0.007184 * W^0.425 * H^0.725

以及

Haycock 公式：BSA = 0.024265 * W^0.5378 * H^0.3964

其中 W 是患者的體重（公斤），H 是身高（釐米），BSA 以平方米表示。對於成人來說，這些公式給出了相當相似的 BSA 估計值，例如，對於體重為 69 公斤，身高為 163 釐米的患者，兩者之間的差異約為 2%，因此在這種應用中，它們的選擇結果並不重要，無論它們是否準確。

總之，商業半自動腎臟分析軟體通常基於以下兩種方法之一

• 確定每個腎臟的 MAG3 的絕對攝取量，並將這些攝取量與從有限患者研究中得出的經驗關係聯絡起來（例如，在 Itoh 等人的情況下，可能是 36 名假設是日本人的患者））
• 確定每個腎臟的 MAG3 攝取率，並將這些攝取率與從有限患者研究中得出的經驗關係聯絡起來（例如，在 Oriuchi 等人的情況下，可能是 12 名假設是日本人的患者））。

鑑於顯而易見的強經驗特徵和調查的患者數量非常有限，有必要評估這些方法的準確性。可以使用蒙特卡洛模擬腎臟顯像 進行此類評估，下表顯示了此類評估的結果

使用兩種不同商業軟體包對六個虛擬腎臟顯像的五種不同分析方法估算的 MAG3 清除率和分割函式的比較。

對於此評估，Itoh ERPF (MAG3)、Inoue (無樣本 MAG3) 和 Oriuchi 清除率 (MAG3) 方法的公式 用於使用電子表格軟體計算每個腎臟顯像的 MAG3 清除率和分割函式。使用製造商的軟體包直接計算 ERPF 修正 Schlegel 和 ERPF 修正 Gates 方法的這些引數值，並假設 ERPF 轉換因子為 0.76（即 Oriuchi 研究的平均值） - Itoh 方法也是如此。

很明顯，所有結果中都沒有相關性，例如，當 MAG3 清除率從 260 毫升/分鐘減半到 130 毫升/分鐘時，計算出的清除率也會降低 - 儘管在某些情況下，修正 Schlegel 方法的結果相當合理。第二個要點是，分割函式估計的變化可能部分是由於使用了（可能是不準確的）自動腎臟深度確定方法。

那麼......這些自動計算是否應該在沒有例如來自橫斷掃描、腎臟顯像後或超聲掃描的腎臟深度測量結果的確認的情況下進行臨床應用？這個問題在 1985 年得到了解答，但不幸的是，這個問題似乎還沒有滲透到現代腎臟分析軟體生產商的心理。

另一個問題：商業雙頭伽馬相機軟體包是否應該考慮將共軛成像用於腎臟顯像分析？

腎臟顯像中的共軛成像

共軛成像的原理基於計算來自兩個相對探測器的活性測量的幾何平均值，並在以下圖表中說明，其中一個均勻介質（黃色矩形）包含一個放射性點源（紅色點）。介質的厚度為 d，點源距離探測器 #1 為 t₁，距離探測器 #2 為 t₂。

共軛計數。

假設沒有檢測到散射，探測器 #1 檢測到的活性由下式給出

$A_{1}=A\exp(-\mu *t_{1})$

而探測器 #2 檢測到的活性由下式給出

$A_{2}=A\exp(-\mu *t_{2})$.

檢測到的活性的幾何平均值 GM 由下式給出

$GM={\sqrt {A_{1}*A_{2}}}$

以便

$GM={\sqrt {A\exp(-\mu *t_{1})*A\exp(-\mu *t_{2})}}$

因此

$GM={\sqrt {A\exp(-\mu *t_{1})*A\exp(-\mu *(d-t_{1}))}}$

因此

$GM={\sqrt {A\exp(-\mu *d)}}$

該最終方程表明幾何平均值僅取決於介質厚度 d，該介質包含點源，而不依賴於源到任一探測器的距離。

將此翻譯成腎圖術意味著使用相對的伽馬相機頭成像（如雙相機 SPECT 系統）將提供獨立於腎臟深度的分離功能測量值。

腎圖術中的共軛成像由以下蒙特卡羅模擬腎圖影像說明，這些影像使用前後（AP）和後前（PA）投影同時獲取。模擬的腎臟深度左側為 7.31 釐米，右側為 8.64 釐米，真實的 LK/RK 分離功能比率為 50%：50%。

左側為前後（AP），右側為後前（PA）蒙特卡羅模擬腎圖。原始資料由 dynamicrenalstudy.org 提供。

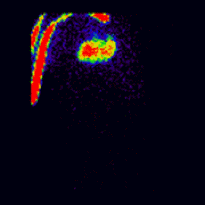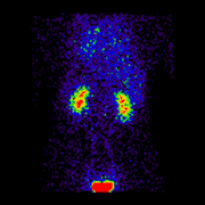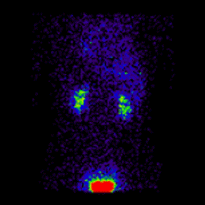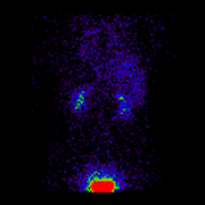
幾何平均腎圖

幾何平均腎圖的曲線。

這些影像用於使用 ImageJ 計算幾何平均值，並使用 OsiriX 分析所得影像。影像計算涉及將 AP 和 PA 腎圖相乘，並以 32 位精度取結果的平方根。計算後的影像被轉換為 16 位以進行 DICOM 儲存。所得幾何平均腎圖（見上面的中心面板）提供了 LK/RK 分離功能估計值為 51%：49%，而未校正腎臟深度的僅 PA 資料提供了較差的估計值為 54%：46%。

從上面的說明可以看出，共軛成像在臨床腎圖術中可能發揮作用，並且可能不依賴於腎臟深度測量進行衰減校正。但是，應該注意的是，該方法假設活動位於具有空間均勻線性衰減係數 μ 的均勻介質中，這表明該方法在真實患者中可能會受到來自諸如覆蓋腎臟的消化氣體等來源的像差的影響。

作為總結，應該注意的是，共軛計數在使用靜態 ^99mTc-DMSA 影像進行定量腎臟分析中已得到充分確立。

血液池補償用於分離功能測定

最近的一篇出版物介紹了血液池補償技術，用於在腎圖術中確定分離功能。這裡，在腎圖的攝取階段，會隨時間測量每個腎臟和肝臟的活動。假設肝臟活動代表腎圖攝取階段的血液池活動。然後，對肝臟活動與腎臟活動圖的線性擬合進行反外推，使其回到零肝臟活動，以確定零血液池貢獻的腎臟活動。然後使用該零活動時的相對貢獻來計算分離功能。

以下圖形說明了這種簡單的方法。在左上角面板中顯示了為肝臟、左腎臟和右腎臟定義的三個感興趣區域 (ROI)，表中的右上角面板顯示了三個所得曲線，用於具有 50/50 分離功能的蒙特卡羅模擬腎圖。在左下角面板中顯示了攝取階段的肝臟計數與腎臟計數圖，其中左腎臟的截距為 17,281 計數，右腎臟的截距為 18,719 計數。然後估計分離功能，左側為 48%，右側為 52%。

右下角面板顯示了平均絕對 % 誤差，該誤差從一系列此類模擬影像中計算得出，其中左腎臟與右腎臟的分離功能從 100%：0% 開始，以 5% 的步長遞增至 50%：50% 再到 0%：100%，結果為 7.5%。