電路理論/傳遞函式目標

戴維南/諾頓阻抗完全表徵了電路從負載的角度來看。微分方程完全描述了電路。電路的脈衝響應是使用卷積積分所需的全部資訊。相量和複頻完全描述了電路。即使在計算瞬態響應時，也出現了與穩態正弦響應相關的複頻。它們之間有關係嗎？是的。

目標是將上述所有內容理解為傳遞函式。為什麼？大多數工程使用這個概念。以下是一些電氣應用

目標是在電子學背景下介紹傳遞函式。

傳遞函式定義

傳遞函式是系統輸出與系統輸入之比。如果我們有一個輸入函式 X(s) 和一個輸出函式 Y(s)，我們定義傳遞函式 H(s) 為

H(s)={Y(s) \over X(s)}

在 RLC 電路中，傳遞函式是相量/複頻/拉普拉斯域的概念。它們不是時域概念。它們獨立於激勵函式/源。有四種可能的 RLC 傳遞模式

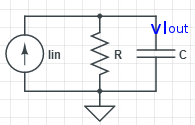傳遞函式有很多應用，我們很快就會看到。但它最直接的好處是消除了查詢微分方程的必要性。回顧前面的例子

例子	微分方程	傳遞函式
卷積積分問題給定電壓源，求總電流	: $v(t)=L{di(t) \over dt}+Ri(t)$	導納: $H(s)={\frac {\mathbb {I} (s)}{\mathbb {V} (s)}}={\frac {1}{sL+R}}$
二階，源激勵求 i_o 給定 Is	$I_{s}={d^{2}i_{o} \over dt^{2}}+2{di_{o} \over dt}+2i_{o}$	分流 $H(s)={\frac {\mathbb {I} _{o}(s)}{\mathbb {I} _{s}(s)}}={\frac {\frac {1}{R+Ls}}{{\frac {1}{R+Ls}}+{\frac {1}{R}}+Cs}}$ $H(s)={\frac {\mathbb {I} _{o}(s)}{\mathbb {I} _{s}(s)}}={\frac {1}{s^{2}+2s+2}}$ R :=1; L :=1; C :=1; simplify((1/(R + Ls))/(1/(R + Ls) + 1/R + C*s))
二階，源激勵給定 V_s，求 V_cr	$V_{s}(t)=L{d({\frac {V_{CR}}{R}}) \over dt}+LC{d^{2}(V_{CR} \over dt^{2}})+V_{CR}$	分壓器 $H(s)={\frac {\mathbb {V} _{cr}(s)}{\mathbb {V} _{s}(s)}}={\frac {\frac {1}{{\frac {1}{R}}+Cs}}{{\frac {1}{{\frac {1}{R}}+Cs}}+Ls}}$ $H(s)={\frac {1}{CLs^{2}+{\frac {Ls}{R}}+1}}$

找到傳遞函式後，下一步是找到時間常數或複頻根，並根據這些推測解的形式。

齊次解是透過將傳遞函式的分母設定為零來找到的。對分母進行因式分解並找到複頻根被稱為找到“零點”。

分子（在所有上述例子中都是 1）可能有一個複頻多項式（在複雜的電路中），它也可以被設定為零。根被稱為“極點”。極點影響電路對不同頻率的響應，而不是時域響應。

這標誌著常規電路理論課程的結束。時域分析可以繼續，在下例中有所提示。二戰之前，為了用模擬計算機模擬物理系統，繼續進行時域分析非常重要。但如今，數字計算機可以更精確地進行建模。因此，在此停止時域分析，並將進一步研究留給專門的課程。讓我們總結一下我們在時域中關於電路的學習內容。

疊加原理允許將多個電源替換為一次一個電源（將其他電源歸零），然後將所有電源的結果相加。
阻抗、導納、分壓器和分流器公式直接得出微分方程...這與相量/複頻域和拉普拉斯變換域的數學相同。
卷積積分消除了將驅動函式（特別是正弦函式）轉換為相量/複頻域/拉普拉斯變換域的需要。相反，電源被替換為 1 伏或 1 安，特解變成一個直流最終條件（t = ∞），放在齊次解上，並在微分方程常數中出現。