工程熱力學/熱力學系統
一般來說,系統是指一組物體,定義系統的方式很微妙,就像集合論一樣。然而,在熱力學中,它是一個更加直接的概念。
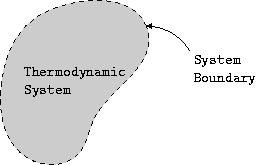
熱力學**系統**是指佔據一定體積並具有邊界的空間區域或有限量。**環境**是指系統外部的任何事物。將系統與其環境隔開的虛線稱為**邊界**。邊界定義了系統的範圍。邊界可以是固定的,也可以是移動的。系統及其環境一起構成了**宇宙**。
有時使用**控制體積**代替系統。在封閉系統的情況下,系統內部物質的質量保持不變,控制體積稱為**控制質量**。控制體積被**控制面**包圍。
接下來,通用術語系統將用於指代熱力學系統。
孤立系統是不允許與環境交換質量或能量的系統。孤立系統根本不與其環境相互作用。系統的邊界不允許質量或能量傳遞。
保溫瓶是孤立系統的近似模型,它透過真空邊界來減緩液體與外部空氣之間的相互作用,從而保持液體的溫度。唯一真正的孤立系統是宇宙。
封閉熱力學系統是指允許與環境交換熱量和功,但不允許任何質量跨越邊界的系統。由於邊界沒有流動,因此這種型別的系統也稱為非流動系統。帶有氣缸的往復式發動機的氣缸和活塞是封閉系統的示例。另一個簡單的例子是水壺,其中熱量被供應到水壺,但其中包含的水量保持恆定。
開放熱力學系統是指允許與環境交換質量和能量的系統。系統內部的質量會隨時間變化。開放系統也稱為控制體積。
空氣壓縮機是開放系統的示例,它從環境中吸入空氣,將其壓縮到高壓,然後透過噴嘴從系統中釋放。
絕熱系統是指允許與環境交換功但不允許交換熱的系統。系統透過熱絕緣邊界來實現這一點。
連續體是指包含連續物質分佈的系統。連續體將系統中的物質視為均勻分佈在空間中,並且不考慮單個原子或分子的作用。壓力、溫度和其他性質是許多原子和分子共同性質的平均值。
物質在其物理結構和化學組成上是均勻的,稱為其相。最常見的相是固態、液態和氣態。
均相系統僅由單一相組成。純物質和均相混合物是均相系統的例子。
非均相系統由兩種或多種不同相組成。
對性質的簡單回顧將向學生介紹熱力學的變數。物質的性質是指質量、溫度、體積和壓力等。性質用於定義物質的當前狀態。熱力學中存在幾個其他性質來描述物質,但需要對理論有更深入的瞭解才能對其進行定義和應用。
性質可以是密集的,如果它們是點性質(對點有意義的性質)或廣泛的,如果它們取決於系統中物質的數量。系統廣泛性質的例子包括系統的質量、系統中物質的摩爾數以及系統的總體積或總積。這些性質取決於您測量系統的多少物質。密集性質的例子包括壓力、溫度、密度、每單位質量的體積、摩爾體積(即每摩爾的體積)以及平均分子量(或分子質量)。這些性質與您如何改變物質質量無關。
性質就像物質的變數,因為它們的值都透過一個方程相關聯。性質之間的關係以方程的形式表達,稱為狀態方程。也許最著名的狀態方程是理想氣體定律。理想氣體定律將理想氣體的壓力、體積和溫度相互關聯。
體積的 SI 單位為m3。
體積是一個廣泛的性質,但每單位質量的體積和摩爾體積都是密集的性質,因為它們不依賴於系統測量的質量。體積保持恆定的過程稱為等容(或等容)過程。
壓力的 SI 單位為 Pa(帕斯卡),相當於。壓力是一個密集的性質。壓力保持恆定的過程稱為等壓過程。
溫度,物體的冷熱程度,被定義為。根據熱力學第零定律,是熱力學的基本概念。我們知道,溫度高的物體將能量轉移到溫度低的物體。考慮兩個溫度不同的物體相互接觸。淨能量轉移將從較熱的物體轉移到較冷的物體。在某一點,淨能量轉移將為零,並且物體被認為處於熱平衡狀態。處於熱平衡狀態的物體被定義為具有相同的溫度。
經典熱力學處理的是處於平衡狀態的系統。平衡狀態由系統中可觀察量的值定義。這些被稱為系統性質。
描述系統所需的最小變數數量取決於系統的複雜性或自由度。自由度是指在系統中可以相互獨立改變的性質的數量。一些常見的系統變數是壓力、溫度和密度,儘管可以使用任何其他物理性質。
與學科發展的公理性質一致,許多物理性質之間的關係無法在沒有進一步理論發展的情況下完全指定。經典熱力學的好處是,這裡陳述的許多公理可以使用統計熱力學技術推匯出。統計熱力學在許多情況下給出了經典熱力學無法給出結果的地方,例如在具有許多自由度的氣體的比熱中。在某種意義上,經典熱力學與統計熱力學之間的關係類似於經典力學與量子力學之間的關係,即,經典熱力學在宏觀極限情況下近似於統計熱力學。
系統狀態的變化稱為過程。當過程的初始狀態和最終狀態相同時,該過程稱為迴圈。如果一個過程可以反轉執行而系統+環境沒有發生變化,則該過程稱為可逆過程。如果一個過程不可逆,則稱為不可逆過程。
等溫過程是指溫度保持恆定的過程。請注意,一個過程是等溫的並不意味著任何關於傳遞的熱量或所做的功,即,在等溫過程中可能會發生熱量傳遞。等溫過程意味著對於理想氣體,體積和壓力的乘積是恆定的。即 PV = 常數
如果系統A與另一個系統B以及第三個系統C處於熱平衡狀態,那麼所有系統彼此都處於熱平衡狀態。這被稱為熱力學第零定律。這就是溫度計的工作原理。如果將溫度計放入物質中進行溫度測量,溫度計的玻璃會與物質達到熱平衡。然後玻璃會與溫度計內部的液體(汞、酒精等...)達到熱平衡。因為物質與玻璃處於熱平衡狀態,而玻璃與內部液體處於熱平衡狀態,所以根據第零定律,物質和液體必須處於熱平衡狀態。並且因為它們熱力學等效,所以它們必須具有相同的溫度。
溫度是透過觀察系統隨溫度變化的某些性質來測量的。這樣的性質稱為測溫性質,例如
- 大多數液體的體積隨溫度升高而增大。
- 金屬棒的長度隨溫度升高而增大。
- 恆定體積氣體的壓力隨溫度升高而增大
建立一個溫度刻度很有用,以便可以在不同溫度下的各種系統之間建立基數關係。這是透過定義溫度t作為測溫性質X的函式來實現的,使得溫度是X的線性函式,即,性質X的相等變化會導致溫度的相等變化。這樣的線性函式是t = a + b X,為此需要將任意溫度分配給X的兩個值以找到常數a和b的值。
例如,在攝氏刻度的情況下,測量基於水在沸點和熔點時的性質。假設測溫性質的值對於正常沸點為Xb,對於正常熔點為Xm。則溫度由t = 100 (X - Xm)/(Xb - Xm)給出,其中X是溫度為t時的測溫性質,我們選擇了tm = 0 °C 和tb = 100 °C。正常熔點和沸點是在 1 個大氣壓壓力下的熔點和沸點溫度。
主要的溫度刻度是攝氏 (°C)、華氏 (°F) 和開爾文 (K) 刻度。注意開爾文沒有°符號——它不是開爾文度,而是開爾文,拼寫時不使用大寫字母,並使用英語的正常複數形式,該複數形式在開爾文作為修飾該單位的形容詞時新增到度中。
不同的溫度計用於不同的溫度範圍。正如讀者可能現在已經猜到的那樣,這意味著不同的溫度計只會同意固定點。但是,已經仔細選擇和校準了一組溫度計,因此在實踐中這不是一個大問題。
在這種情況下,標準是國際溫標,該溫標於 1927 年引入,並在 1948 年、1968 年和 1990 年進行了修訂。最新的刻度用開爾文刻度的T90表示,從 0.65 K 向上定義。例如,在 0.65 K 到 5.0 K 之間,T90 是根據3He 和4He 的蒸氣壓溫度關係來定義的。不同材料的範圍重疊,任何有效的材料都可以在重疊區域用作標準。
回顧一下,熱力學系統可能包含某種物質,其數量可以用質量或摩爾數來表示,並佔據一定的體積。這些是系統的廣延性質。如果物質在所討論的體積內均勻分佈,那麼每物質量的體積值可以作為強度性質使用。例如,對於一個稱為“摩爾”的量,每摩爾的體積通常被稱為“摩爾體積”。類似地,某種物質的每單位質量的體積可能被稱為比容。在這種情況下,狀態方程可以用來聯絡三個強度性質:溫度、壓力和摩爾體積或比容。
一個簡單但非常有用的狀態方程是理想氣體的狀態方程。理想氣體在熱力學中是一個非常有用的概念,因為它是一個只依賴於兩個獨立性質的簡單系統。理想氣體是指在除與其他分子完全彈性碰撞之外,沒有其他分子間相互作用的氣體。對於包含理想氣體的封閉系統,其狀態可以透過給出壓力、溫度和摩爾體積中的任何兩個值來確定。
考慮一個系統,一個封閉在容器中的理想氣體。從初始狀態 1 開始,氣體的溫度為 T1,透過恆壓過程將溫度改變為 T2,然後進行恆摩爾體積過程,則發現壓力的比率與摩爾體積的比率相同。假設初始壓力和摩爾體積的值分別為 p1 和 V1,最終壓力和摩爾體積的值分別為 p2 和 V2。需要注意的是,我們還沒有選擇溫度的特定標度(例如攝氏溫標)。現在,假設我們選擇一個標度,使得 T1/T2 = p1/p2,我們可以證明對於理想氣體,pV/T 的值是恆定的,因此它遵循氣體方程 pV = RT,其中 p 是絕對壓力,V 是摩爾體積,R 是一個稱為“普適氣體常數”的常數。溫度 T 是理想氣體溫標中的絕對溫度,該溫標與熱力學溫標一致。熱力學溫標將在熱力學第二定律的陳述之後定義。
這個方程 pV = RT 被稱為理想氣體的狀態方程,也被稱為理想氣體方程。大多數常見的氣體在沒有被壓縮或冷卻到極端狀態的情況下,都遵循理想氣體方程,因此這是一個非常有用的關係式。我們可以寫一個類似的方程,其中對於特定型別的氣體,使用比容代替摩爾體積,並使用特定氣體常數代替普適氣體常數。這樣寫成 pv = mrT。
在上圖中,理想氣體在兩個不同壓力 p1 和 p2 下的體積,針對攝氏溫度進行了繪製。如果我們外推這兩條直線圖,它們會在溫度軸上相交於一點 t0,其中 t0 = −273.15 °C。
透過實驗,很容易證明熱力學溫度 T 與攝氏溫度 t 之間的關係為:T = t + 273.15。熱力學溫標的零點是 0 K,當我們討論熱力學第二定律時,它的意義將變得清晰。