定義

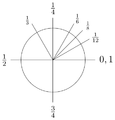
以周為單位測量的角度
倍增對映

角度倍增對映^[1]^[2]

T(r)=(2r){\bmod {1}}

輸入：真分數 $r$ 的形式

十進位制比率（如果 r 不是無理數）
十進位制數字序列和基數
二進位制數字序列和基數

輸出：真分數

二進位制分數上的倍增對映

倍增對映 d 對分數 x 的二進位制表示的影響是簡單地移位 x 的位到左側，丟棄移位到一位的位 = 左移。^[3]

$x=0.b_{1}b_{2}b_{3}\dots .$

$d(x)=0.b_{2}b_{3}\dots .$

示例

$2*{\frac {11}{31}}=2*0.01011=0.10110={\frac {22}{31}}$

軌道

對映的迭代給出軌道（角度序列）

週期性（輸入是有奇數分母的有理數 $d=2^{p}-1$ ）
前週期性（輸入是有偶數分母的有理數）
非週期性（當輸入是無理數時）

以上所有型別都是無限的。有限二進位制展開具有相等的無限前週期表示。

週期性

角度在倍增對映下的週期軌道

注意，這裡連線單位圓上 2 個點 z1 和 z2 的弦意味著 $z_{2}=z_{1}^{2}$ 。它並不意味著這些點是同一條射線的著陸點。

有些軌道不會交叉

週期為 2 的軌道（角度在倍增對映下）
週期為 3 的軌道（角度在倍增對映下）
週期為 4 的軌道（角度在倍增對映下）
週期為 5 的軌道（角度在倍增對映下）
週期為 6 的軌道（角度在倍增對映下）
週期 9

但有些軌道會交叉

11/63 在倍增對映下的週期為 6 的軌道
74/511 在倍增對映下的週期為 9 的軌道

角度 $r={\frac {n}{d}}$ 的週期軌道，其中分母 d 為奇數

 $r={\frac {n}{d}}={\frac {n}{2^{p}-1}}$

其中

n 是分數的分子 = 從 0 到 (d-1) 的整數
d 是分數的分母 = 正整數
p 是週期 = 正整數

週期為 1（1 個軌道）的角度 = ${\frac {n}{2^{1}-1}}={\frac {n}{1}}$

{0/1 = 1/1 }

週期 2 (1 軌道) 對應角度 = ${\frac {n}{2^{2}-1}}={\frac {n}{3}}$

{1/3, 2/3}

週期 3 (2 軌道) 對應角度 = ${\frac {n}{2^{3}-1}}={\frac {n}{7}}$

{1/7, 2/7, 4/7 }
{3/7, 6/7, 5/7 }

週期 4 (3 軌道) 對應角度 = ${\frac {n}{2^{4}-1}}={\frac {n}{15}}$

{1/15,  2/15,  4/15,  8/15 }
{3/15,  6/15, 12/15,  9/15 }
{7/15, 14/15, 13/15, 11/15 }

週期 5 (6 軌道) 對應角度 = ${\frac {n}{2^{5}-1}}={\frac {n}{31}}$

{ 1/31,  2/31,  4/31,  8/31, 16/31}
{ 3/31,  6/31, 12/31, 24/31, 17/31}
{ 5/31, 10/31, 20/31,  9/31, 18/31}
{ 7/31, 14/31, 28/31, 25/31, 19/31}
{11/31, 22/31, 13/31, 26/31, 21/31}
{15/31, 30/31, 29/31, 27/31, 23/31}

週期 6 (9 軌道) 對應角度 = ${\frac {n}{2^{6}-1}}={\frac {n}{63}}$ , 僅分子

{ 1, 2, 4, 8,16,32}
{ 3, 6,12,24,48,33}
{ 5,10,20,40,17,34}
{ 7,14,28,56,49,35}
[11,22,44,25,50,37}
[13,26,52,41,19,38}
[15,30,60,57,51,39}
[23,46,29,58,53,43]
[31,62,61,59,55,47]

週期 = 7 對應角度 = ${\frac {n}{2^{7}-1}}={\frac {n}{127}}$

週期 = 8 對應角度 = ${\frac {n}{2^{8}-1}}={\frac {n}{255}}$

週期 = 9 對應角度 = ${\frac {n}{2^{9}-1}}={\frac {n}{511}}$

參見

引數平面上的根點（鍵點）的外部射線
動態平面
- 落在拋物固定點上的外部射線。（第一個角度是尾流的角度）

前週期

這裡分數 r 的分母 d

r={\frac {n}{d}}

是偶數

d=2^{t}q

並且 q 是奇數。

這裡

t 是前週期

示例軌道

前週期 1 和週期 1 對應角度 ${\frac {n}{2}}$

{1/2 , (0/2)}

參見

Misiurewicz 點在引數平面上
動態平面上的樹枝狀朱利亞集

非週期

比較

實現

整數
- 2 個整數（分子和分母）
- 有理數
  - GMP 庫中的 mpq 型別
浮點數
- double

向前

使用 32 位有符號整數將最大前週期限制在約 30
使用 double 表示分數將最大精確位數限制在約 53 位

C 使用整數

#include <stdio.h>
#include <stdlib.h> // malloc
#include <limits.h> // INT_MAX
#include <assert.h>
#include <math.h>

/* 

 gcc d.c -Wall -Wextra -lm
 
 
 example input fractions
 wikibooks Fractals/Mathematics/binary
 
*/

int nMax;

/*
https://stackoverflow.com/questions/19738919/gcd-function-for-c
The GCD function uses Euclid's Algorithm. 
It computes A mod B, then swaps A and B with an XOR swap.
*/
int gcd(int a, int b)
{
    int temp;
    while (b != 0)
    {
        temp = a % b;

        a = b;
        b = temp;
    }
    return a;
}


/*
 n/d -> n_new/d_new
 
*/

int give_reduced_fraction(const int n, const int d, int * n_new, int *d_new){


	int divisor = gcd(n,d);
	if (divisor != 1) {
		*n_new = n / divisor;
		*d_new = d / divisor;}
		
		else {
			*n_new = n;
         		*d_new = d;
		}
	return 0;
}
/*
Binary expansion can be :
* finite - decimal ratio number with even denominator which is a power of 2. Note that it has also equal infinite preperiodic representation
* infinite
** periodic : preperiod = 0, period > 0, rational number with odd denominator which is not a power of 2
** preperiodic ( = eventually periodic) : preperiod > 0, period > 0, rational number with even denominator
** aperiodic : preperiod = 0, period = 0 ( or infinity), irrational number

input is a rational number t = n/d so 
here  are only 2 types of result:
* 0 = preperiodic ( = eventually periodic) : preperiod > 0, period > 0, rational number with even denominator
* 1 = periodic : preperiod = 0, period > 0, rational number with odd denominator which is not a power of 2
*/

int give_dynamic_type(const int n, const int d){

	// boolean flag
	int is_odd = 0;
	int is_POT = 0;
	
	if (d % 2) 
		{	// d % 2 > 0  	
			fprintf(stdout, "denominator %d is odd\n", d); // parzysty
			is_odd = 1;
		
		}
		else { // d % 2  = 0 
			fprintf(stdout, "denominator %d is even\n", d); // nieparzysty
			is_odd = 0;
		}
		
	if (d>0 && ((d & (d-1)) == 0))
		{ 
			fprintf(stdout, "denominator %d is power of 2 ( POT) = 2^%d\n", d, (int) log2(d));
			is_POT = 1;}
		else { 
			fprintf(stdout, "denominator %d is not the power of 2\n", d);
			is_POT = 0;}
	
	// wikibooks Fractals/Mathematics/binary#preperiod_and_period
	if ( is_odd == 0 && is_POT == 1)
		{
			fprintf(stdout, "Binary expansion of %d/%d is finite and has equal infinite preperiodic representation\n", n,d);
			//fprintf(stdout, "denominator is even and POT\n");
			return 0;
			}
	
	// preperiodic ( = eventually periodic) : preperiod > 0, period > 0, rational number with even denominator
	if (is_odd == 0 && is_POT == 0) 
		{
			fprintf(stdout, "Binary expansion of %d/%d is preperiodic\n", n,d);
			//fprintf(stdout, "denominator is even and not POT\n");
			return 0;
		}
	
	// periodic : preperiod = 0, period > 0, rational number with odd denominator which is not a power of 2
	if (is_odd == 1 && is_POT == 0) 
		{
			fprintf(stdout, "Binary expansion of %d/%d is periodic\n", n,d);
			//fprintf(stdout, "denominator is not even (odd) and not POT\n");
			return 1;
		}
		
		
	return 0;
}




int give_period(const int n0, const int d0){

	int n = n0;
	int d = d0;
	
	int i;
	int iMax = 20; // period_max 
	
	int period = 0;

	// printf(" i\t numerator/denominator \n"); // header 

	for ( i=0 ; i< iMax; i++){
		// printf("%3d:\t %3d / %3d \n", i, n, d);
     
     
		// check signed integer overflow before it will happen
		if ( n > nMax ) 
		{printf(" signed integer overflow will happen = wrap; use extended precision \n"); return 1;}
                               
		// angle doubling map modulo 1 
		n = 2*n;
		n = n % d;   
		 // 
		if (n == n0) {
			period = i+1; 
			// printf(" preperiod = 0 and period of fraction under doubling map is %d\n", period); 
			return period;}
	
	}
	return 0; // period not found, maybe period > iMax
}

int give_periodic_orbit(const int period, int n, int d,  int orbit[]){
	
	int i;
	int iMax = period; // 
	for ( i=0 ; i< iMax; i++){
		orbit[i] = n;
     
     
		// check signed integer overflow before it will happen
		if ( n > nMax ) 
		{printf(" signed integer overflow will happen = wrap; use extended precision \n"); return 1;}
                               
		// angle doubling map modulo 1 
		n = 2*n;
		n = n % d;   
		 
	}
	return 0;


}

int give_preperiod(const int period, const int n0, const int d0,  int orbit[]){

	int n = n0;
	int d = d0;
	
	int i;
	int iMax = period; // 
	for ( i=0 ; i< iMax; i++){
		if (orbit[i] == n) return i;
		// angle doubling map modulo 1 
		n = 2*n;
		n = n % d; }
		
	return 0;

}




/*
input : reduced proper rational fraction in t = n0/d0
output
* perperiod as a result
* period as a pointer

*/
int give_preperiod_and_period(const int n0, const int d0, int *period){
	
	int n = n0;
	int d = d0;
	
	*period = 0;
	int preperiod = 0;
	int preperiod_max = 1000; 
	if ( preperiod_max > INT_MAX  - *period ){printf("give_preperiod_and_period error: preperiod_max > INT_MAX  - period, signed integer overflow will happen = ; use extended precision \n"); return -1;}
	
	
	int i;
	int iMax = preperiod_max; // preperiod_max 
	
	// go thru preperiodic part to periodic part
	for ( i=0 ; i< iMax; i++){
		//printf("%3d:\t %3d / %3d \n", i, n, d);
     
     
		// check signed integer overflow before it will happen
		if ( n > nMax ) 
		{printf("give_preperiod_and_period error: signed integer overflow will happen = wrap; use extended precision \n"); return 1;}
                               
		// angle doubling map modulo 1 
		n = 2*n;
		n = n % d; }
	
	// now it should be periodic part 
	
	*period = give_period (n,d);
	
	// periodic orbit
	int *orbit; // only numerators
	orbit = (int *) malloc( *period * sizeof(* orbit)); 
	give_periodic_orbit(*period, n, d, orbit);
	
	
	preperiod = give_preperiod( *period, n0, d0,  orbit);
	
	
	
	
	free(orbit);
	
	return preperiod;
}


void give_orbit(const int n0, const int d0, const int preperiod, const int period){

	int n = n0;
	int d = d0;

	int i;
	int iMax = preperiod+period; // preperiod_max 
	
	
	
	for ( i=0 ; i< iMax; i++){
		if ( i < preperiod) 
			{ printf("%3d:\t %3d / %3d \t preperiodic part \n", i, n, d);}
			else {printf("%3d:\t %3d / %3d \t periodic part \n", i, n, d);}
			

		// angle doubling map modulo 1 
		n = 2*n;
		n = n % d; }
		
		
	
}



/*
Algorithm:[36]

Multiply the input decimal fraction by two
from above result
take integer part as the binary digit
take the fractional part as the starting point for the next step
repeat until you either get to 0 or a periodic number
read the number starting from the top - the first binary digit is the first digit after the comma

*/
void print_binary_expansion(const int n0, const int d0, const int preperiod, const int period){

	int n = n0;
	int d = d0;
	
	int i_max = preperiod+period;
	int i;
	double t = (double) n/d;
	double t_fractional;
    	double t_integer;
    	
    	int binary_digit;

    	
	printf("formated infinite binary expansion of %d/%d is 0.",  n0,d0);
	for (i = 0; i < i_max; ++i){
	
		// doubling map
		t *= 2.0; 
				
		// split 
		t_fractional = modf(t, &t_integer);
	
		//
		binary_digit = (int) t_integer;
		
		if (i== preperiod) {printf("(");}
		printf("%d", binary_digit);
		
		// take the fractional part as the starting point for the next step
		t = t_fractional;
		
		
		
	
	}
	printf(")\n");



}


int describe_fraction(const int n0, const int d0){

	// proper decimal fraction
	// t = n/d 
	//int n0 = 1; // 
	//int d0 = 66; // 
	
	// tr = n0r/d0r = t after reduction
	int n0r ; // 
	int d0r ; // 

	int n;
	int d;
	
	
	int period = 0;  
	int preperiod = 0;

	
	assert(n0 > 0);
	assert(d0 > 1);
	assert(n0 < d0);  // proper fraction



	// ------------ 	Reducing Fractions to Lowest Terms -------------------------------
	//  ----------- wikipedia Irreducible_fraction ----------------------------
	give_reduced_fraction(n0, d0, &n0r, &d0r);
	
	if (n0 == n0r && d0 ==d0r )
		{printf(" fraction = %d/%d\t is irreducible = in lowest terms \n", n0, d0 ); }
		else {printf(" fraction = %d/%d\t after reduction is %d/%d \n", n0, d0, n0r,d0r); }
	
	
	n = n0r;
	d = d0r;

	assert(n > 0);
	assert(d > 1);
	assert(n < d);

	int type = give_dynamic_type(n,d);
	
	
	// ------------------compute preperiod and period under doubling map -------------------------
	printf("fraction %d/%d under doubling map has: \n", n0r, d0r);
	if (type ==0 ){
		
		preperiod = give_preperiod_and_period( n0r, d0r, &period);
		
		if (preperiod > 0) {
			printf("\t preperiod = %d and period  = %d\n", preperiod, period);
			if (period == 0 )
				{printf("period = 0 means period NOT  FOUND !!!\n\t  maybe period > iMax in give_period \n\tor maybe preperiod_max in give_preperiod_and_period is to big \n");}}}
			
		 // --------------
		
		else { 
			period = give_period(n,d);
			if (period > 0)
				{printf(" preperiod = 0 and period = %d\n", period); }
				else {printf(" preperiod = 0 and period of fraction under doubling map > 0 but  period NOT  FOUND !!!  maybe period > iMax in give_period \n");}}
	// -------------------------------------------------
	
	
	give_orbit( n0, d0, preperiod, period);
	
	// ----------formated infinite binary expansion ---------------------
	print_binary_expansion( n0r, d0r, preperiod, period);
	return 0;

}

int main(void) {

	nMax = INT_MAX / 2; // signed integer 
	
	describe_fraction(1,22);


		

	return 0; 
}

使用雙精度數的 C 語言

使用雙精度數可以得到精度為 53 位二進位制數擴充套件（雙精度浮點數的精度位數）。

t *= 2.0; // t = 2*t
if (t > 1.0) t--; // t = t modulo 1

/*

*/
#include <stdio.h> // printf
#include <math.h> // fabs


#define iMax  8 //

int main(){

	double t0 ;
	double t ;
	double ti; // final t after iMax iterations
	double tr; //
	double dt;
	
	int itinerary[iMax]= {0};
	
	
	
	
	
	int i;
	
	
	t0 = (double) 1/7;
	t = t0;
	
	// check the input : it should be   0.0 <= t < 1.0
	if (t>1.0) {printf("t is > 1.0\n"); return 1;}
	if (t<0.0) {printf("t is < 0.0\n"); return 1;}
	
	
	printf("forward iteration of doubling map\n");
	for(i=0; i<iMax; i++){
	        
	        printf("t%d = %f", i, t);
	       
		t = t*2.0; // doubling 
		if (t>1.0) {	
			
			itinerary[i]= 1;
			t = t - 1.0; 
			printf(" wrap\n");} // modulo 1 
			else printf("\n");
		}
	printf("t%d = %f\n", i, t);	
		
	//		
	ti = t;	
	
	printf("\nbackward iteration of doubling map = halving map \n");
	
	//
	for(i=iMax; i>0; i--){ // reverse counting
	        
	        printf("t%d = %f", i, t);
	        
	        if (itinerary[i-1]==1) { // i-1 !!! 
	        	 
	        	t = t + 1.0; 
	        	printf(" unwrap\n");} // modulo 1 
			else printf("\n");
	        t = t/2.0; // halving 
		
		}
	printf("t%d = %f\n", i, t);	
		
			
         tr = t;		
		
		
	//
	printf("\n\nresults \n");
	printf("t0 = %f\n", t0);	
	printf("t%d = %f\n", iMax, ti);
	
	dt = fabs(t0- tr);
	printf("tr = %f\n", tr);
	printf("dt = fabs(t0- tr) = %f\n", dt );
	printf("\nitinerary:\n");
	for(i=0; i<iMax; i++) printf("itinerary[%d] = %d \n", i, itinerary[i]);
	
	
	printf("\ndecimal %f has binary expansion = 0.", t0);
	for(i=0; i<iMax; i++) printf("%d", itinerary[i]);
	printf("\n");
	
	if (dt < 0.0000000001) printf("program works good !\n");
		else printf("program fails !\n");
	
		

	return 0;}

使用 GMP 庫中的有理數型別 mpq 的 C 語言（任意精度）

C 函式（使用 GMP 庫）^[4]

// rop = (2*op ) mod 1 
void mpq_doubling(mpq_t rop, const mpq_t op)
{
  mpz_t n; // numerator
  mpz_t d; // denominator
  mpz_inits(n, d, NULL);

 
  //  
  mpq_get_num (n, op); // 
  mpq_get_den (d, op); 
 
  // n = (n * 2 ) % d
  mpz_mul_ui(n, n, 2); 
  mpz_mod( n, n, d);
  
      
  // output
  mpq_set_num(rop, n);
  mpq_set_den(rop, d);
    
  mpz_clears(n, d, NULL);

}

/*

C programme using gmp  

gcc r.c -lgmp

http://gmplib.org/manual/Rational-Number-Functions.html#Rational-Number-Functions


*/



#include <stdio.h>
#include <gmp.h>

// input = num/den
unsigned int num = 1;
unsigned int den = 6;

int main ()
{
        
        
        
        
        mpq_t q;   // rational number; 
        int b =2 ; // base of numeral system
        mpz_t  n ;
        mpz_t  d ;
        mpf_t  f ;
        char  *sr;
        char  *sf;
        mp_exp_t exponent ; // holds the exponent for the result string

        // init and set variables 
        mpq_init (q); // Initialize r and set it to 0/1.
        mpf_init (f);
        mpz_init_set_ui(n,num);
        mpz_init_set_ui(d,den);
        mpq_set_num(q,n);
        mpq_set_den(q,d);
        mpq_canonicalize (q); // It is the responsibility of the user to canonicalize the assigned variable before any arithmetic operations are performed on that variable. 
        mpf_set_q(f,q); 
        
        
        
        // convertions
        sr = mpq_get_str (NULL, b, q); // rational number = fraction : from decimal to binary
        // If str is NULL, the result string is allocated using the current allocation function
        sf = mpf_get_str (NULL, &exponent, b, 0, f); // floating point number : from decimal to binary
        //  If n_digits is 0 then that accurate maximum number of digits are generated. 
        
        // print 
        gmp_printf ("a rational number %Zd / %Zd is in a canonical form ( decimal fraction) : %Qd\n",n,d, q); // 
        gmp_printf(" numerator of rational number = %Zd \n", mpq_numref(q)); //
        gmp_printf(" denominator of rational number = %Zd \n", mpq_denref(q)); //
        gmp_printf ("  binary rational (  string ) : %s \n", sr); // 
        gmp_printf ("  decimal floating point number : %.Ff \n", f); // 
        
        // The output of the GMP programme is in the form mantissa,'e',exponent where the value is
        // 0.mantissa * 2^exponent
        // GMP represents the floating point numbers (for base 2) as a pair of exponent  and mantissa (and sign). 
        
        //The generated string is a fraction, with an implicit radix point immediately to the left of the first digit. 
        //  Trailing zeros are not returned.
        // For example, the number 3.1416 would be returned as string "31416" and exponent 1 so :
        // 3.1416 = 0.31416*10^1
        // another example : 1/6 as a exponential form of binary  number will be :
        // mantissa = 101010101010101010101010101010101010101010101010101010101010101011
        // exponet = -2
        // so 1/6 = 0.101010101010101010101010101010101010101010101010101010101010101011 * 2 ^(-2) = 0.0(01) 
        gmp_printf ("  mantissa of binary floating (  string ) : %s \n", sf); //  
        gmp_printf ("  exponent : %ld \n", exponent); //
        printf ("binary floating number in exponential form =0.%s*%d^%ld\n", sf,b, exponent); 
        
        
        // clear memory
        mpq_clear (q);
        mpz_clear (n);
        mpz_clear (d);
        mpf_clear (f);
        
        return 0;
}

編譯

gcc r.c -lgmp

執行

./a.out

結果

a rational number 1 / 6 is in a canonical form ( decimal fraction) : 1/6
numerator of rational number = 1 
denominator of rational number = 6 
 binary rational (  string ) : 1/110 
 decimal floating point number : 0.166666666666666666667 
 mantissa of binary floating (  string ) : 101010101010101010101010101010101010101010101010101010101010101011 
 exponent : -2 
binary floatin in exponential form =0.101010101010101010101010101010101010101010101010101010101010101011*2^-2

Maxima CAS

使用分子和分母作為輸入的 Maxima CAS 函式

doubling_map(n,d):=mod(2*n,d)/d $

或使用有理數作為輸入

DoublingMap(r):=
  block([d,n],
        n:ratnumer(r),
        d:ratdenom(r),
        mod(2*n,d)/d)$

Common Lisp 函式

(defun doubling-map (ratio-angle)
" period doubling map =  The dyadic transformation (also known as the dyadic map, 
 bit shift map, 2x mod 1 map, Bernoulli map, doubling map or sawtooth map "
(let* ((n (numerator ratio-angle))
       (d (denominator ratio-angle)))
  (setq n  (mod (* n 2) d)) ; (2 * n) modulo d
  (/ n d))) ; result  = n/d

Haskell

Haskell 函式^[5]

-- by Claude Heiland-Allen
-- type Q = Rational
 double :: Q -> Q
 double p
   | q >= 1 = q - 1
   | otherwise = q
   where q = 2 * p

C++

//  mndcombi.cpp  by Wolf Jung (C) 2010. 
//   http://mndynamics.com/indexp.html 
// n is a numerator
// d is a denominator
// f = n/d is a rational fraction (angle in turns)
// twice is doubling map = (2*f) mod 1
// n and d are changed (arguments passed to function by reference)

void twice(unsigned long long int &n, unsigned long long int &d)
{  if (n >= d) return;
   if (!(d & 1)) { d >>= 1; if (n >= d) n -= d; return; }
   unsigned long long int large = 1LL; 
   large <<= 63; //avoid overflow:
   if (n < large) { n <<= 1; if (n >= d) n -= d; return; }
   n -= large; 
   n <<= 1; 
   large -= (d - large); 
   n += large;
}

倍增對映的反函式

每個角度 α ∈ R/Z（以轉數表示）都具有

一個像 = 2α mod 1 在倍增對映下
“在倍增對映下有兩個原像：α/2 和 (α + 1)/2。”^[6] 倍增對映的反函式是一個多值函式。

在 Maxima CAS 中

InvDoublingMap(r):= [r/2, (r+1)/2];

請注意這兩個原像之間的差

{\frac {\alpha }{2}}-{\frac {\alpha +1}{2}}={\frac {1}{2}}

是半圈 = 180 度 = Pi 弧度。

倍增對映 d 下的像和原像
$\alpha$	$d^{1}(\alpha )$	$d^{-1}(\alpha )$
${\frac {1}{2}}$	${\frac {1}{1}}$	$\left\{{\frac {1}{4}},{\frac {3}{4}}\right\}$
${\frac {1}{3}}$	${\frac {2}{3}}$	$\left\{{\frac {1}{6}},{\frac {4}{6}}\right\}$
${\frac {1}{4}}$	${\frac {1}{2}}$	$\left\{{\frac {1}{8}},{\frac {5}{8}}\right\}$
${\frac {1}{5}}$	${\frac {2}{5}}$	$\left\{{\frac {1}{10}},{\frac {6}{10}}\right\}$
${\frac {1}{6}}$	${\frac {1}{3}}$	$\left\{{\frac {1}{12}},{\frac {7}{12}}\right\}$
${\frac {1}{7}}$	${\frac {2}{7}}$	$\left\{{\frac {1}{14}},{\frac {4}{7}}\right\}$

問答

分析

查詢擴充套件型別
查詢前週期和週期
轉換十進位制小數為二進位制展開式
格式化展開式

如何查詢擴充套件型別

十進位制小數的二進位制展開式

/*
 gcc i.c -Wall -Wextra -lm

 https://stackoverflow.com/questions/108318/how-can-i-test-whether-a-number-is-a-power-of-2
 (n>0 && ((n & (n-1)) == 0))

 https://stackoverflow.com/questions/160930/how-do-i-check-if-an-integer-is-even-or-odd
if (x % 2) {  } //  x is odd 
 An integer is even if it is a multiple of two, power of 2, true if num is perfectly divisible by 2 :  mod(24,2) = 0
 and odd if it is not.

*/


#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <assert.h>




int main(void)
{
	int n = 1;
	int d = 4; // 
	// boolean flag
	int is_odd = 0;
	int is_POT = 0;
	//int type; 
	
	//
	assert( n > 0); 
	assert( d > 0);
	assert( n < d); // proper fraction
	
	
	if (d % 2) 
		{	// d % 2 > 0  	
			fprintf(stdout, "denominator %d is odd\n", d); // parzysty
			is_odd = 1;
		
		}
		else { // d % 2  = 0 
			fprintf(stdout, "denominator %d is even\n", d); // nieparzysty
			is_odd = 0;
		}
		
	if (d>0 && ((d & (d-1)) == 0))
		{ 
			fprintf(stdout, "denominator %d is power of 2 ( POT) = 2^%d\n", d, (int) log2(d));
			is_POT = 1;}
		else { 
			fprintf(stdout, "denominator %d is not the power of 2\n", d);
			is_POT = 0;}
	
	// https://wikibook.tw/wiki/Fractals/Mathematics/binary#preperiod_and_period
	if ( is_odd == 0 && is_POT == 1)
		{
			fprintf(stdout, "Binary expansion of %d/%d is finite and has equal infinite representation\n", n,d);
			fprintf(stdout, "denominator is even and POT\n");
			}
	
	// preperiodic ( = eventually periodic) : preperiod > 0, period > 0, rational number with even denominator
	if (is_odd == 0 && is_POT == 0) 
		{
			fprintf(stdout, "Binary expansion of %d/%d is preperiodic\n", n,d);
			fprintf(stdout, "denominator is even and not POT\n");
		}
	
	// periodic : preperiod = 0, period > 0, rational number with odd denominator which is not a power of 2
	if (is_odd == 1 && is_POT == 0) 
		{
			fprintf(stdout, "Binary expansion of %d/%d is periodic\n", n,d);
			fprintf(stdout, "denominator is not even (odd) and not POT\n");
		}	
		
		
	return 0;
}

如何查詢前週期和週期？

週期和倍增對映

如何查詢週期角度下的倍增對映

視覺
數值
- 從十進位制小數的分母（約化有理分數 m/n）中讀取週期
- 在二進位制展開式（二進位制序列）中查詢週期/前週期
  - 字串匹配演算法，例如，樸素或暴力搜尋，Knuth-Morris-Pratt 演算法^[7]
  - 離散傅立葉變換
- 從角度在倍增對映下的行程中讀取它

約化有理分數 m/n 的二進位制展開式的週期等於2 模n 的乘法階

$Period_{2}(m/n)={ord}_{n}(2)$

角度 5/31 在倍增對映下的軌道

C 版本

雙精度：正向和逆向倍增對映

/*


doubling map 


2*t mod 1 



how to invert doubling map  



Inverse of doubling map is multivalued function: 2 preimages
t/2 and  (t+1)/2
to choose proper preimage one needs extra information from forward iteration = itinerary





itinerary : list of symbols 
for  coding the orbits of a given dynamical system 
by partitioning the space X and forming an itinerary 



http://www.maths.qmul.ac.uk/~sb/cf_chapter4.pdf


see also how to convert proper decimal fraction to binary fraction

commons :Binary_decomposition_of_dynamic_plane_for_f0(z)_%3D_z%5E2.png



---------- git -------------------- 
cd existing_folder
git init
git remote add origin git@gitlab.com:adammajewski/doubling_map.git
git add .
git commit -m "Initial commit"
git push -u origin master



*/
#include <stdio.h> // printf
#include <math.h> // fabs


#define iMax  8 //

int main(){

	double t0 ;
	double t ;
	double ti; // final t after iMax iterations
	double tr; //
	double dt;
	
	int itinerary[iMax]= {0};
	
	
	
	
	
	int i;
	
	
	t0 = (double) 1/7;
	t = t0;
	
	// check the input : it should be   0.0 <= t < 1.0
	if (t>1.0) {printf("t is > 1.0\n"); return 1;}
	if (t<0.0) {printf("t is < 0.0\n"); return 1;}
	
	
	printf("forward iteration of doubling map\n");
	for(i=0; i<iMax; i++){
	        
	        printf("t%d = %f", i, t);
	        // wikipedia Dyadic_transformation
		t = t*2.0; // doubling 
		if (t>1.0) {	
			
			itinerary[i]= 1;
			t = t - 1.0; 
			printf(" wrap\n");} // modulo 1 
			else printf("\n");
		}
	printf("t%d = %f\n", i, t);	
		
	//		
	ti = t;	
	
	printf("\nbackward iteration of doubling map = halving map \n");
	
	//
	for(i=iMax; i>0; i--){ // reverse counting
	        
	        printf("t%d = %f", i, t);
	        
	        if (itinerary[i-1]==1) { // i-1 !!! 
	        	 
	        	t = t + 1.0; 
	        	printf(" unwrap\n");} // modulo 1 
			else printf("\n");
	        t = t/2.0; // halving 
		
		}
	printf("t%d = %f\n", i, t);	
		
			
         tr = t;		
		
		
	//
	printf("\n\nresults \n");
	printf("t0 = %f\n", t0);	
	printf("t%d = %f\n", iMax, ti);
	
	dt = fabs(t0- tr);
	printf("tr = %f\n", tr);
	printf("dt = fabs(t0- tr) = %f\n", dt );
	printf("\nitinerary:\n");
	for(i=0; i<iMax; i++) printf("itinerary[%d] = %d \n", i, itinerary[i]);
	
	
	printf("\ndecimal %f has binary expansion = 0.", t0);
	for(i=0; i<iMax; i++) printf("%d", itinerary[i]);
	printf("\n");
	
	if (dt < 0.0000000001) printf("program works good !\n");
		else printf("program fails !\n");
	
		

	return 0;}

任意精度

// gcc d.c -lgmp -Wall

#include <stdio.h>
#include <gmp.h>

//  a multiple precision integer, as defined by the GMP library. The C data type for such integers is mpz_t

int print_z(mpz_t  z, int base, char *s){
  printf("%s= ", s);
  mpz_out_str (stdout, 10, z);
  printf (" for base = %d\n", base);
  return 0;
}

// rop = (2*op) mod 1
// wikipedia : dyadic_transformation or doubling map
void mpq_doubling(mpq_t rop, const mpq_t op)
{
  mpz_t n; // numerator
  mpz_t d; // denominator
  mpz_inits(n, d, NULL);

 
  //  
  mpq_get_num (n, op); // 
  mpq_get_den (d, op); 
 
  // n = (n * 2 ) % d
  mpz_mul_ui(n, n, 2); 
  mpz_mod( n, n, d);
  
      
  // output
  mpq_set_num(rop, n);
  mpq_set_den(rop, d);
    
  mpz_clears(n, d, NULL);

}

int main ()
{

        int i;
        //
        unsigned long int e = 89; // exponent is also a period of doubling map 
        unsigned long int b = 2;
       
        // arbitrary precision variables from GMP library
        mpz_t  n ; // numerator of q
        mpz_t  d ; // denominator of q
        mpq_t q;   // rational number q = n/d

        // init and set variables 
        mpz_init_set_ui(n, 1);

        // d = (2^e) -1 
        // http://fraktal.republika.pl/mset_external_ray.html
        mpz_init(d);
        mpz_ui_pow_ui(d, b, e) ;  // d = b^e
        mpz_sub_ui(d, d, 1);   // d = d-1

        //   q = n/d
        mpq_init (q); //
        mpq_set_num(q,n);
        mpq_set_den(q,d);
        mpq_canonicalize (q); // It is the responsibility of the user to canonicalize the assigned variable before any arithmetic operations are performed on that variable.

        // print 
        //print_z(d, 10, "d ");
        //print_z(n, 10, "n ");
        gmp_printf ("q = %Qd\n",q); //  
        
        // 
        for (i=0; i<(1+2*e) ; i++){  
          mpq_doubling(q, q);
          gmp_printf ("q = %Qd\n",q); // 
        }   
         
       
        
        
        // clear memory
        mpq_clear (q);
        mpz_clears(n, d, NULL);
        
        
        return 0;
}

C++ 版本

/*
based on : 
   mndcombi.cpp  by Wolf Jung (C) 2010. 
   http://mndynamics.com/indexp.html 
   which is the part of Mandel 5.5 
   multiplatform C++ GUI program using QT 
   on the same licence as above

 "The function is computing the preperiod and period (of n/d under doubling map)
 and setting the denominator to  2^preperiod*(2^period - 1) if possible.
 So 1/5 becomes 3/15 and 2/10 becomes 3/15 as well.
 The period is returned as the value of the function, 
 n and d are changed ( Arguments passed to function by reference)
 and the preperiod is returned in k." (Wolf Jung)
 Question : if result is >=0 why do not use unsigneg char or unsigned int for type of result ???

*/
int normalize(unsigned long long int &n, unsigned long long int &d, int &k)
{  if (!d) return 0; // d==0 error
   n %= d; 
   while (!(n & 1) && !(d & 1)) { n >>= 1; d >>= 1; }
   int p; 
   unsigned long long int n0, n1 = n, d1 = d, np;
   k = 0; 
   while (!(d1 & 1)) { k++; d1 >>= 1; if (n1 >= d1) n1 -= d1; }
   n0 = n1;
   for (p = 1; p <= 65 - k; p++) 
	{ twice(n1, d1); 
	  if (n1 == n0) break; }
   if (k + p > 64) return 0; // more then max unsigned long long int
   np = 1LL; 
   np <<= (p - 1); 
   np--; np <<= 1; 
   np++; //2^p - 1 for p <= 64
   n0 = np; 
   d >>= k; n1 = d; 
   if (n1 > n0) { n1 = n0; n0 = d; }
   while (1) { d1 = n0 % n1; if (!d1) break; 
   n0 = n1; n1 = d1; } //gcd n1
   n /= d/n1; 
   n *= np/n1; 
   d = np << k;
   return p;
}

Lisp 版本

(defun give-period (ratio-angle)
	"gives period of angle in turns (ratio) under doubling map"
	(let* ((n (numerator ratio-angle))
	       (d (denominator ratio-angle))
	       (temp n)) ; temporary numerator
	  
	  (loop for p from 1 to 100 do 
		(setq temp  (mod (* temp 2) d)) ; (2 x n) modulo d = doubling)
		when ( or (= temp n) (= temp 0)) return p )))

Maxima CAS 版本

DoublingMap(r):=
block([d,n],
 n:ratnumer(r),
 d:ratdenom(r),
 mod(2*n,d)/d)$

/*
Tests : 
GivePeriod (1/7)
3
GivePeriod (1/14) 
0
GivePeriod (1/32767)
15
GivePeriod (65533/65535)
16

Gives 0 if :
* not periodic ( preperiodic )
* period >pMax
*/

GivePeriod (r):=
block([rNew, rOld, period, pMax, p],
      pMax:100,
      period:0,
       
      p:1, 
      rNew:DoublingMap(r),
      while ((p<pMax) and notequal(rNew,r)) do
        (rOld:rNew,
         rNew:DoublingMap(rOld),
         p:p+1
        ),
      if equal(rNew,r) then period:p,
      period
);

Haskell 版本

Haskell 版本^[8]

從整數型別（Int 或 Integer）到任何其他型別的轉換透過“fromIntegral”完成。目標型別會自動推斷

-- by Claude Heiland-Allen
-- import Data.List (findIndex, groupBy)
-- type N = Integer
-- type Q = Rational
 period :: Q -> N
 period p =
  let Just i = (p ==) `findIndex` drop 1 (iterate double p)
  in  fromIntegral i + 1

轉換

所有十進位制小數都能精確地轉換為二進位制嗎？

並非所有小數都能精確地轉換為二進位制。只有分母為 2 的冪 (有限) 的那些小數才具有精確的十進位制表示。“在其他所有情況下，表示中都會存在誤差。誤差的大小取決於用於表示它的位數。” ^[9]

十進位制轉換為二進位制

#include <stdio.h>
#include <stdlib.h> // malloc
#include <limits.h> // INT_MAX
#include <assert.h>
#include <math.h>

/* 

 gcc d.c -Wall -Wextra -lm
 
 
 example input fractions in wikibooks
 /Fractals/Mathematics/binary
 
*/

int nMax;

/*
https://stackoverflow.com/questions/19738919/gcd-function-for-c
The GCD function uses Euclid's Algorithm. 
It computes A mod B, then swaps A and B with an XOR swap.
*/
int gcd(int a, int b)
{
    int temp;
    while (b != 0)
    {
        temp = a % b;

        a = b;
        b = temp;
    }
    return a;
}


/*
 n/d -> n_new/d_new
 
*/

int give_reduced_fraction(const int n, const int d, int * n_new, int *d_new){


	int divisor = gcd(n,d);
	if (divisor != 1) {
		*n_new = n / divisor;
		*d_new = d / divisor;}
		
		else {
			*n_new = n;
         		*d_new = d;
		}
	return 0;
}
/*
Binary expansion can be :
* finite - decimal ratio number with even denominator which is a power of 2. Note that it has also equal infinite preperiodic representation
* infinite
** periodic : preperiod = 0, period > 0, rational number with odd denominator which is not a power of 2
** preperiodic ( = eventually periodic) : preperiod > 0, period > 0, rational number with even denominator
** aperiodic : preperiod = 0, period = 0 ( or infinity), irrational number

input is a rational number t = n/d so 
here  are only 2 types of result:
* 0 = preperiodic ( = eventually periodic) : preperiod > 0, period > 0, rational number with even denominator
* 1 = periodic : preperiod = 0, period > 0, rational number with odd denominator which is not a power of 2
*/

int give_dynamic_type(const int n, const int d){

	// boolean flag
	int is_odd = 0;
	int is_POT = 0;
	
	if (d % 2) 
		{	// d % 2 > 0  	
			fprintf(stdout, "denominator %d is odd\n", d); // parzysty
			is_odd = 1;
		
		}
		else { // d % 2  = 0 
			fprintf(stdout, "denominator %d is even\n", d); // nieparzysty
			is_odd = 0;
		}
		
	if (d>0 && ((d & (d-1)) == 0))
		{ 
			fprintf(stdout, "denominator %d is power of 2 ( POT) = 2^%d\n", d, (int) log2(d));
			is_POT = 1;}
		else { 
			fprintf(stdout, "denominator %d is not the power of 2\n", d);
			is_POT = 0;}
	
	//  wikibooks: Fractals/Mathematics/binary#preperiod_and_period
	if ( is_odd == 0 && is_POT == 1)
		{
			fprintf(stdout, "Binary expansion of %d/%d is finite and has equal infinite preperiodic representation\n", n,d);
			//fprintf(stdout, "denominator is even and POT\n");
			return 0;
			}
	
	// preperiodic ( = eventually periodic) : preperiod > 0, period > 0, rational number with even denominator
	if (is_odd == 0 && is_POT == 0) 
		{
			fprintf(stdout, "Binary expansion of %d/%d is preperiodic\n", n,d);
			//fprintf(stdout, "denominator is even and not POT\n");
			return 0;
		}
	
	// periodic : preperiod = 0, period > 0, rational number with odd denominator which is not a power of 2
	if (is_odd == 1 && is_POT == 0) 
		{
			fprintf(stdout, "Binary expansion of %d/%d is periodic\n", n,d);
			//fprintf(stdout, "denominator is not even (odd) and not POT\n");
			return 1;
		}
		
		
	return 0;
}




int give_period(const int n0, const int d0){

	int n = n0;
	int d = d0;
	
	int i;
	int iMax = 20; // period_max 
	
	int period = 0;

	// printf(" i\t numerator/denominator \n"); // header 

	for ( i=0 ; i< iMax; i++){
		// printf("%3d:\t %3d / %3d \n", i, n, d);
     
     
		// check signed integer overflow before it will happen
		if ( n > nMax ) 
		{printf(" signed integer overflow will happen = wrap; use extended precision \n"); return 1;}
                               
		// angle doubling map modulo 1 
		n = 2*n;
		n = n % d;   
		 // 
		if (n == n0) {
			period = i+1; 
			// printf(" preperiod = 0 and period of fraction under doubling map is %d\n", period); 
			return period;}
	
	}
	return 0; // period not found, maybe period > iMax
}

int give_periodic_orbit(const int period, int n, int d,  int orbit[]){
	
	int i;
	int iMax = period; // 
	for ( i=0 ; i< iMax; i++){
		orbit[i] = n;
     
     
		// check signed integer overflow before it will happen
		if ( n > nMax ) 
		{printf(" signed integer overflow will happen = wrap; use extended precision \n"); return 1;}
                               
		// angle doubling map modulo 1 
		n = 2*n;
		n = n % d;   
		 
	}
	return 0;


}

int give_preperiod(const int period, const int n0, const int d0,  int orbit[]){

	int n = n0;
	int d = d0;
	
	int i;
	int iMax = period; // 
	for ( i=0 ; i< iMax; i++){
		if (orbit[i] == n) return i;
		// angle doubling map modulo 1 
		n = 2*n;
		n = n % d; }
		
	return 0;

}




/*
input : reduced proper rational fraction in t = n0/d0
output
* perperiod as a result
* period as a pointer

*/
int give_preperiod_and_period(const int n0, const int d0, int *period){
	
	int n = n0;
	int d = d0;
	
	*period = 0;
	int preperiod = 0;
	int preperiod_max = 1000; 
	if ( preperiod_max > INT_MAX  - *period ){printf("give_preperiod_and_period error: preperiod_max > INT_MAX  - period, signed integer overflow will happen = ; use extended precision \n"); return -1;}
	
	
	int i;
	int iMax = preperiod_max; // preperiod_max 
	
	// go thru preperiodic part to periodic part
	for ( i=0 ; i< iMax; i++){
		//printf("%3d:\t %3d / %3d \n", i, n, d);
     
     
		// check signed integer overflow before it will happen
		if ( n > nMax ) 
		{printf("give_preperiod_and_period error: signed integer overflow will happen = wrap; use extended precision \n"); return 1;}
                               
		// angle doubling map modulo 1 
		n = 2*n;
		n = n % d; }
	
	// now it should be periodic part 
	
	*period = give_period (n,d);
	
	// periodic orbit
	int *orbit; // only numerators
	orbit = (int *) malloc( *period * sizeof(* orbit)); 
	give_periodic_orbit(*period, n, d, orbit);
	
	
	preperiod = give_preperiod( *period, n0, d0,  orbit);
	
	
	
	
	free(orbit);
	
	return preperiod;
}


void give_orbit(const int n0, const int d0, const int preperiod, const int period){

	int n = n0;
	int d = d0;

	int i;
	int iMax = preperiod+period; // preperiod_max 
	
	
	
	for ( i=0 ; i< iMax; i++){
		if ( i < preperiod) 
			{ printf("%3d:\t %3d / %3d \t preperiodic part \n", i, n, d);}
			else {printf("%3d:\t %3d / %3d \t periodic part \n", i, n, d);}
			

		// angle doubling map modulo 1 
		n = 2*n;
		n = n % d; }
		
		
	
}



/*
Algorithm:[36]

Multiply the input decimal fraction by two
from above result
take integer part as the binary digit
take the fractional part as the starting point for the next step
repeat until you either get to 0 or a periodic number
read the number starting from the top - the first binary digit is the first digit after the comma

*/
void print_binary_expansion(const int n0, const int d0, const int preperiod, const int period){

	int n = n0;
	int d = d0;
	
	int i_max = preperiod+period;
	int i;
	double t = (double) n/d;
	double t_fractional;
    	double t_integer;
    	
    	int binary_digit;

    	
	printf("formated infinite binary expansion of %d/%d is 0.",  n0,d0);
	for (i = 0; i < i_max; ++i){
	
		// doubling map
		t *= 2.0; 
				
		// split 
		t_fractional = modf(t, &t_integer);
	
		//
		binary_digit = (int) t_integer;
		
		if (i== preperiod) {printf("(");}
		printf("%d", binary_digit);
		
		// take the fractional part as the starting point for the next step
		t = t_fractional;
		
		
		
	
	}
	printf(")\n");



}


int describe_fraction(const int n0, const int d0){

	// proper decimal fraction
	// t = n/d 
	//int n0 = 1; // 
	//int d0 = 66; // 
	
	// tr = n0r/d0r = t after reduction
	int n0r ; // 
	int d0r ; // 

	int n;
	int d;
	
	
	int period = 0;  
	int preperiod = 0;

	
	assert(n0 > 0);
	assert(d0 > 1);
	assert(n0 < d0);  // proper fraction



	// ------------ 	Reducing Fractions to Lowest Terms -------------------------------
	//  ----------- wikipedia Irreducible_fraction ----------------------------
	give_reduced_fraction(n0, d0, &n0r, &d0r);
	
	if (n0 == n0r && d0 ==d0r )
		{printf(" fraction = %d/%d\t is irreducible = in lowest terms \n", n0, d0 ); }
		else {printf(" fraction = %d/%d\t after reduction is %d/%d \n", n0, d0, n0r,d0r); }
	
	
	n = n0r;
	d = d0r;

	assert(n > 0);
	assert(d > 1);
	assert(n < d);

	int type = give_dynamic_type(n,d);
	
	
	// ------------------compute preperiod and period under doubling map -------------------------
	printf("fraction %d/%d under doubling map has: \n", n0r, d0r);
	if (type ==0 ){
		
		preperiod = give_preperiod_and_period( n0r, d0r, &period);
		
		if (preperiod > 0) {
			printf("\t preperiod = %d and period  = %d\n", preperiod, period);
			if (period == 0 )
				{printf("period = 0 means period NOT  FOUND !!!\n\t  maybe period > iMax in give_period \n\tor maybe preperiod_max in give_preperiod_and_period is to big \n");}}}
			
		 // --------------
		
		else { 
			period = give_period(n,d);
			if (period > 0)
				{printf(" preperiod = 0 and period = %d\n", period); }
				else {printf(" preperiod = 0 and period of fraction under doubling map > 0 but  period NOT  FOUND !!!  maybe period > iMax in give_period \n");}}
	// -------------------------------------------------
	
	
	give_orbit( n0, d0, preperiod, period);
	
	// ----------formated infinite binary expansion ---------------------
	print_binary_expansion( n0r, d0r, preperiod, period);
	return 0;

}

int main(void) {

	nMax = INT_MAX / 2; // signed integer 
	
	describe_fraction(1,22);


		

	return 0; 
}

精度

我需要什麼型別精度的數字來計算倍增對映？

“倍增對映每次迭代都會損失一位精度。”^[10]
將角度儲存為精確的有理數 (例如，使用 libgmp 的 mpq_t) 使其能夠精確到超過 53 次迭代 (雙精度浮點數的精度位數)。僅在需要使用 sin 和 cos 來尋找目標點時才轉換為 double。double 對目標點來說已經足夠精確。Claude Heiland-Allen^[11]

參見

二進位制小數

參考文獻

[1] 關於對映 x↦kx (mod Z) 週期軌道的組合型別。第一部分：實現作者：Carsten L. Petersen，Saeed Zakeri

[2] Mark McClure 的 chaos_and_doubling 對映

[3] Mark McClure 的倍增對映

[4] 波蘭華夏公益教科書中的 UNIX 系統程式設計：GMP

[5] Claude Heiland-Allen 使用 Haskell 和 SVG 輸出的 lavaurs 演算法

[6] 符號動力學和自相似群，作者：VOLODYMYR NEKRASHEVYCH

[7] th stackexchange 問題：有限二進位制序列的週期

[8] Claude Heiland-Allen 使用 Haskell 和 SVG 輸出的 lavaurs 演算法

[9] Davide Borchia 的二進位制小數計算器

[10] Mark McClure 的混沌與分形。2.11 關於計算的一些說明

[11] ractalforums.org : 使用牛頓法求解引數外部射線

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]