交通經濟學/定價

定價

定價的理由

道路擁堵、汽車尾氣汙染以及缺乏為新的地面交通選擇籌集資金的資源，都帶來了挑戰。道路定價，即在行駛時間之外，對使用者徵收貨幣通行費，被認為是解決這些問題的方案。雖然通行費在隧道和橋樑等某些昂貴設施中很常見，但在街道和高速公路上卻不太常見。在美國和其他地方，正在部署新一代私人收費公路。新加坡、倫敦和斯德哥爾摩等地進行過一些區域定價方案的試驗，還有許多其他方案被提議但尚未實施。

簡而言之，定價可以實現幾個目標

• 收入
• 擁堵管理 - 交通擁堵在大城市和主要高速公路上很常見。它既耗時，又給乘客和貨物運輸帶來大量的不可確定性和煩惱。大多數交通擁堵都是由旅行者自私的行為造成的（參見關於路線選擇的討論），因為他們會給其他人帶來延誤，並且沒有支付他們旅行的全部邊際成本。在經濟學中，這被稱為負外部性。為了解決這個問題，一些經濟學家建議對擁堵徵稅。在第一版教科書《福利經濟學》中，庇古（1920）主張對擁堵徵稅，從而開創了擁堵定價的文獻。大多數經濟學家支援擁堵定價作為緩解困境的好方法，但許多人對實施的細節表示擔憂。擁堵收費分配擁堵地區和高峰時段的稀缺道路容量。電子收費系統 (ETC) 和自動車輛識別 (AVI) 技術允許在不延誤旅行者的情況下完成此操作。
• 路面管理 - 路面損壞取決於每軸車輛重量，而不是總車輛重量 - 損壞力隨著每軸負荷的立方呈指數增長（例如，一輛典型 13 噸貨車的後軸造成的損壞是轎車的 1000 多倍）。為了更準確地反映路面損壞成本，Small 和 Winston (1989) 提出了一項“基於軸重的分級每英里稅”。這將鼓勵卡車司機（卡車製造商）透過轉向更多軸的卡車來減少軸重，延長路面使用壽命並減少公路維護。目前實施的燃油稅給卡車司機帶來了相反的激勵措施：該稅隨著車輛軸數的增加而增加，因為更多軸的卡車需要更大的發動機，燃油效率也更低。他們指出，美國州際公路與運輸官員協會 (AASHTO) 的路面厚度指南未能將經濟最佳化納入設計程式。例如，將剛性水泥混凝土路面厚度僅從目前的 11.2 英寸增加到 13.8 英寸，就會使路面使用壽命增加一倍以上。
• 解除安裝成本或重新分配成本（改變誰承擔負擔） - 公路成本分配研究定期嘗試更新汽車和各種卡車類別為道路承擔的負擔量，但他們只有兩種政策工具（汽油和柴油稅）來完成這項工作。更強大的定價策略可以使收費更直接地與來源成正比。
• 能源供應的變化表明燃油稅收入下降
• 鼓勵駕駛以外的交通方式

道路定價沒有更普遍的原因有很多。直到最近，技術問題還很突出，收費站增加了相當大的延誤，並且由於需要收費亭裡的人員，淨收入大幅減少。然而，自動車輛識別和收費技術的進步使得能夠在全速行駛的情況下進行收費，無需人工操作。其他問題本質上是政治性的：對隱私、公平以及雙重徵稅的看法感到擔憂。雖然隱私問題是政治問題，但可能存在技術解決方案，例如使用電子貨幣，電子貨幣不會與其所有者相關聯，而不是使用信用卡或簽帳金融卡或自動識別和車輛計費。公平問題，即認為新系統會產生贏家和輸家，可能無法完全解決。儘管可以證明在某些情況下，道路定價對整個社會來說具有淨效益，但除非存在一種機制可以讓足夠多的道路使用者和投票者受益或感覺到受益，否則這種擔憂將成為實施的障礙。同樣，人們可能認為他們已經透過燃油稅和一般收入支付了道路費用，並且對他們收費類似於雙重徵稅。除非使用者能夠相信籌集到的收入用於維護和擴建，或其他令人信服的公共目的，否則政治上的推銷將很困難。廣泛的道路定價可能需要改變一般的交通運輸融資結構，並且需要提供清晰的效益說明。

擁堵定價理論

標題：擁堵定價帶來有效均衡。

每當一種稀缺且有價值的商品（如道路使用）是免費或價格過低時，需求就會超過供應。道路使用方面的說明很明顯，當嘗試在同一時間使用某段道路的駕駛員數量超過道路容量時，就會出現排隊和交通堵塞。除非高峰使用者支付擴建的全部費用，否則擴大容量以滿足高峰需求會導致非高峰時段的浪費性過剩容量。如果我們看一下長途電話服務，分配是透過市場機制決定的，在高峰時段收取高價，在非高峰時段提供折扣。消費者似乎接受了基於市場的長途電話服務需求分配系統，該系統表明該政策有效。

在道路的情況下，需求由擁堵分配。高峰時段對道路使用的過度需求會導致擁堵。經濟學家認為，旅行行為是由旅行的支出加上所需時間的價值決定的。當擁堵變得足夠嚴重時，一些駕駛員會改變他們的旅行時間，但沒有足夠的駕駛員改變他們的旅行時間以完全緩解擁堵。改變旅行時間的駕駛員數量永遠不足以減少擁堵，因為 - 在沒有對道路使用進行某種定價或配額的情況下 - 在高峰時段使用道路的駕駛員無需支付他們互相造成的延誤。

透過讓駕駛員為他們因旅行而給其他人造成的延誤付費，而不是隻支付他們個人的成本，這將促使一些人做出其他選擇。駕駛員可能會決定改變他們的旅行時間，拼車或使用公共交通工具。擁堵定價將允許駕駛員在交通不太擁擠的情況下進行高峰時段的旅行，但前提是他們願意為他們互相造成的延誤付費。價格將設定在將擁堵減少到最有效水平的水平，這可以證明是高峰時段使用一段道路容量的全部貨幣和時間成本。

道路使用者關於在哪裡以及何時使用車輛的決定是透過將他們從使用道路中獲得的利益與其自身成本進行比較來做出的。這些成本不包括他們給其他旅行者或整個社會造成的成本，例如擁堵和環境破壞。這種行為的結果是，旅行的收益低於社會成本。交通量比合理的還多，並且在時間和容量上沒有得到有效的分配。如果人們因其旅行決定而給其他人造成的成本而被收費，那麼將出現導致最佳效率的旅行模式。

替代性收入機制

道路使用者收費可能或多或少是直接的。一般來說，道路收費的間接方法與車輛所有權和使用有關。例如，擁有汽車的固定費用 - 購買新車的購置稅和年度牌照續簽 - 以及汽車使用的可變費用 - 輪胎油和燃料稅。

燃料稅等道路收費的間接方法是當今社會最常用的方法，因為其使用量大，且易於收取。然而，像燃料稅這樣的收入方法很少將資金直接注入專門用於公路維護或開發的道路或交通基金。在由多個道路使用者造成的擁堵情況下，駕駛員會對其他使用者造成邊際社會成本，包括延遲和更高的運營成本，而他們沒有為此支付費用。

直接收費包括監控車輛行駛的實際時間或距離並進行適當的收費。有很多方法可以進行直接收費。隨著電子技術的不斷發展，既可以實施車外收費機制，也可以實施車內收費機制。車外機制包括手動收費站、硬幣式機器和路邊自動掃描器等裝置。車內機制包括磁卡、智慧卡和應答器。

擁堵定價可以採取多種形式。最直接的例子是在現有的收費站上增加額外費用，或者在沒有收費的路線或橋樑上增加高峰時段的收費。收費可以是一個簡單的峰值溢價或非高峰時段折扣，也可以根據特定時間設施所承受的需求進行調整。

在實踐中，擁堵定價可以採取六種形式

• 點收費，即在特定時間經過某個點的公路使用者需要支付通行費，無論其在指定路線上的行駛距離如何；
• 隔離帶收費，即希望進入擁堵區域的使用者需要在每個入口處支付通行費；
• 區域收費，即在隔離帶區域內行駛的使用者也需要支付通行費；
• 在擁堵區域內停車收費更高，尤其是在最擁堵的時間段內停車；
• 擁堵特定收費，即使用者需要根據其花費的時間和行駛距離支付費用。

這些政策對需求的影響不同。一般稅收不能預期會減少對特定旅行的需求。交通特定稅收應該在一定程度上減少需求，但不會減少對特定道路路段的需求，例如擁堵的設施。隔離帶收費將減少穿越隔離帶的需求，但其本質上比“完美收費”目標性更低。雖然不同的融資機制對它們如何影響需求有不同的影響，但它們也有不同的收取成本。歷史上，目標性越強的機制，成本越高。然而，隨著電子收費系統使用範圍的擴大，這些歷史上的普遍規律可能會發生改變。管理政策的管轄範圍級別的變化會改變福利的感知。地方政府對當地居民（即其選民）負責，並且傾向於不關心非當地居民的福利。因此，需要區分面對不同政府層級的激勵結構。當道路由州擁有和運營時，實施產生的福利可能與相同融資機制由擁有和運營道路並可以保留收費收入的區域大都市規劃組織實施時的福利不同。同樣，大都市規劃組織也不同於縣。造成這些差異的主要原因與誰支付通行費以及通行費支付者是否（或在多大程度上）居住在地方政府機構的邊界內有關。縣對非縣居民的經濟福利的關注程度很低，大都市地區對其他地區居民的關注程度也很低。因此，決策權的下放會影響所選擇的政策。

擁堵定價的影響

橋樑和收費公路過去收費變化的證據表明，駕駛員確實對價格的變化做出反應。在談到個人交通需求的價格彈性時，分析表明彈性約為 -0.10 到 -0.15 作為下限，-0.3 到 -0.4 作為上限，具體取決於收費、當前旅行成本以及替代道路和交通系統的容量。價格上漲後，需求會下降，但消費者對道路使用的需求足夠強勁，以至於需求下降的百分比不會像價格上漲的百分比那麼大。

旅行選擇可能會有很多變化，包括

• 路線，從收費路線切換到不收費路線或更快的收費路線。
• 時間，更改出發時間，以避免收費或收費時段。
• 模式，改為或放棄拼車、公共交通或其他模式。
• 目的地，更改非工作活動的目的地，選擇距離更近的位置。
• 地點，搬家或搬遷工作場所以縮短通勤時間。
• 順序，透過將多個差事合併到一次旅行中來連結旅行。
• 頻率，減少不重要的旅行次數
• 存在，透過遠端辦公進行活動以減少工作相關旅行。
• 所有權，駕駛員也可能放棄汽車所有權以避免通行費。

高速公路上的擁堵定價將對整個交通系統產生廣泛的影響，因為它會將對交通服務的需求從高峰時段高速公路的單人駕駛使用中轉移出去。減少高峰時段駕駛的激勵措施將使一些交通轉移到非高峰時段，這將提高道路系統的效率 - 因此，減少對額外容量的需求。一些駕駛員將繼續在高峰時段駕駛，但會選擇與他人拼車或更改行程目的地。與他人拼車也將透過增加高峰時段每輛車的乘客數量來提高系統使用效率。

一些駕駛員會改乘公共交通。擁堵定價帶來的交通流量改善將提高服務可靠性和速度，因此，使公共交通比汽車更具吸引力。公共交通使用量的增加將增加收入。這些收入可以用來增加服務頻率或路線覆蓋範圍。擁堵定價還會減少對新的高速公路開發的需求。這將減少對道路開發的資本支出需求，以應對人口增長和出行需求。

拆解

圖 2 上部示意性地顯示了駕駛員在瓶頸或容量受限路段上，由於各種接近流量水平而產生的行駛時間（短期平均成本）。行駛時間函式將行駛時間（或延遲）和接近交通流量聯絡起來。接近流量越大，行駛時間越長。在低於容量的流量下（服務水平 A（SA）或 B（SB）），交通流量平穩，而在高於容量的高接近流量下，交通流量是停停走走，被歸類為服務水平 E（SE）或 F（SF）。

圖 2 底部示意性地顯示了路段上對旅行的隱含需求，該需求是接近流量的函式。在所有其他條件相同的情況下（例如向使用者收取的價格），服務水平 A（DA）的路段旅行需求高於服務水平 F（DF）的需求。然而，路段上的需求和行駛時間並不獨立，如圖 2（A）所示。

因此，隱含需求和顯露需求並不相同，而是顯露需求是透過將給定流量下的行駛時間投影到隱含需求曲線上形成的。例如，當向使用者收取的價格很高時，顯露需求與服務水平 A（DA）下的隱含需求一致。隨著價格降低，顯露需求在服務水平 B（DB）處與隱含需求曲線交叉，然後是 DC、DD、DE，最後在零貨幣價格時，它與 DF 相交。雖然產生特定需求水平的實際價格因地而異，並受當地情況、需求偏好和市場條件的影響，但總體趨勢（更高的價格導致更低的接近流量導致更好的服務水平）僅僅是經濟學中需求規律與交通流量理論的應用。

換句話說，擁堵定價對福利的影響不僅取決於價格和數量的變化，還取決於保留價格的變化。保留價格是指旅行者在給定服務水平下願意支付的金額。在更好的服務水平下，旅行者（和潛在旅行者）的保留價格更高。

福利分析

沿揭示需求曲線移動遵循上述曲線形狀，這是因為交通流量（需求量）與旅行時間之間的關係。例如，假設每個服務水平類別代表旅行時間比前一個服務水平類別高一分鐘。因此，在圖中，將一分鐘旅程的服務水平表示為 SA，六分鐘旅程的服務水平表示為 SF。從 1 分鐘到 2 分鐘所需的交通流量超過從 2 分鐘到 3 分鐘所需的交通流量。換句話說，在時間方面存在上升的平均（因此是邊際）成本。

圖 2 中的概念可用於制定圖 3 中所示的福利分析。圖 3 中有幾個值得關注的區域。第一個區域由左下角三角形（藍色 + 綠色）（三角形 VOZ）定義，表示道路未定價時的消費者剩餘。第二個區域是道路定價後公路管理部門的生產者剩餘（利潤），由左下角形成的矩形（黃色 + 綠色）（矩形 OVWY）表示。第三個區域是道路定價時的消費者剩餘，用灰色表示（三角形 UVW）。這種消費者剩餘代表了比其他剩餘更高的保留價格，因為當流量較低時，服務水平更高。

第一個區域需要與第二個區域和第三個區域的總和進行比較。如果第二個區域和第三個區域的總和（OUWY）大於第一個區域（OVZ），那麼定價比保持未定價具有更高的福利。類似地，可以比較兩個價格水平。換句話說，定價帶來的福利增益等於黃色 + 灰色區域（VUWX）減去藍色區域（XYZ）。在這個特定的圖中，當商品免費時，消費者剩餘最大化，但整體福利（包括生產者剩餘）並不最大化。在給定情況下，消費者剩餘是否實際上更高，取決於各種需求曲線的斜率。

最大的福利是透過最大化生產者剩餘矩形和消費者剩餘“三角形”（它可能不是真正的三角形）的總和來實現的。這必須認識到消費者剩餘三角形的斜邊必須遵循潛在的需求曲線，而不是揭示的需求曲線。區分服務水平（例如，以兩種不同的價格提供兩種不同的服務水平）可能會導致更高的整體福利（雖然不一定對每個人來說都是更高的福利）。

收入的使用

福利的衡量方式和感知方式是兩回事。如果生產者剩餘沒有以某種方式返還給系統的使用者，使用者將感知到整體福利增益為個人損失，因為它將起著額外的稅收作用。這筆錢可以透過返還其他稅收或再投資於交通運輸的方式返還。應該注意的是，整個論證可以反過來進行，其中消費者和生產者剩餘用時間而不是金錢來衡量，而服務水平是旅行的貨幣成本。然而，這在實踐中應用較少。

定價和成本回收

在低流量的情況下，即沒有擁堵的情況下，邊際成本擁堵定價帶來的收入不太可能收回長期固定成本。這是因為當流量很低時，一輛額外汽車的邊際影響幾乎為零，因此透過邊際成本定價可以籌集的額外收入也為零。想象一下一條只有一輛車的道路——這輛車的邊際影響為零，邊際成本價格也為零，因此其收入為零，小於固定成本。

新增第二輛車，邊際影響仍然幾乎為零——這種現象在接近容量之前一直存在。

維克裡的擁堵型別

• 簡單互動——交通流量小，一輛車被另一輛車擋住，延誤與 Q^2 成正比
• 多重互動——0.5 < V/C < 0.9

$Z=t-t_{o}=1/s-1/s_{o}=ax^{k}$

t 實際時間，to 自由流時間，K ~ 3-5

• 瓶頸見下文
• 觸發頸——溢位影響其他交通
• 網路和控制——交通管制裝置轉移延誤
• 總體密度——總體交通水平高

邊際成本定價

交通運輸是一個廣泛的領域，吸引了具有工程、經濟學和規劃背景的個人，以及其他對交通擁堵沒有共同模型或世界觀的人。經濟學家尋找可以分析的已接受的技術功能，但有誤解它們的風險。工程師尋求基本的經濟概念來管理交通，他們認為這是他們自己的職責範圍。這兩個領域在擁堵定價領域交叉。然而，許多工程師對定價持懷疑態度，認為許多經濟學家高估了它的效力，而經濟學家則對工程的固執感到沮喪，並認為工程師缺乏對基本市場原則的理解。

本節應用了微觀交通擁堵模型，該模型用於擁堵定價，並允許我們批評文獻中出現的幾種擁堵經濟模型的合理性。

本節使用排隊和瓶頸的概念來解釋擁堵。如果沒有瓶頸（可能是物理的和永久性的，例如車道減少或陡坡，或者可變的，例如交通管制裝置，或者由於事故而造成的臨時性），擁堵將很少。在暢通無阻的道路上行駛的車輛會導致相對較小的延誤，並且不再考慮（Vickery 1969，Daganzo 1995）。我們將擁堵或擁堵期定義為存在排隊的時間。這超過了到達量超過離開量的時間，因為每輛車都必須等待所有之前的車輛離開佇列的前部才能離開。

前面一節介紹了擁堵的排隊模型。

單個車輛級別的輸入輸出圖

單個車輛級別的邊際延誤

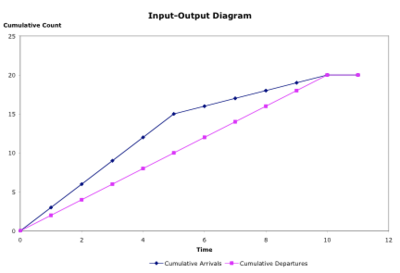
我們的排隊模型對邊際成本定價有何影響？

首先，使用每小時平均時間與流量函式，如公共道路局函式（我們在路線選擇討論中介紹了該函式）（該函式近似於排隊模型的每小時平均延誤），忽略了該小時內不同的車輛具有不同的旅行時間。它們充其量只能用於粗略的宏觀分析，但永遠不應該應用於單個車輛級別。

其次，車輛透過瓶頸的旅行時間取決於之前到達的車輛數量，但與之後到達的車輛數量無關。類似地，一輛車輛造成的邊際延誤只施加在之後的車輛上。這意味著佇列中的第一輛車造成最大的邊際延誤，而佇列中的最後一輛車造成最小的邊際延誤。從右側（頂部）所示的典型輸入輸出圖生成的邊際延誤函式類似於右側（底部）的圖。如果邊際成本等於邊際延誤，那麼我們的定價函式將是不尋常的，甚至可能不穩定。透過讓需求對價格做出反應，而不是假設它是固定的（Rafferty 和 Levinson 2003），以及透過認識到到達和離開模式的隨機性，可能會抑制這種不穩定性，這種隨機性將使到達曲線更平坦，更接近於離開曲線，從而使邊際延誤曲線更平坦。

然而，第一個車輛“導致”延誤的想法是一個有爭議的觀點。經濟學家有時會爭論科斯（1992）的立場——即需要兩個人才會產生負外部性，如果沒有後續車輛的到來，就不會存在擁堵外部性。科斯當然是對的。此外，他們會指出，對後續車輛徵收通行費會阻止該車輛到來，也可能消除擁堵外部性。這也有可能是真的。然而，這將是給擁堵的受害者徵收兩次費用（一次是時間，一次是通行費），而擁有更快的行程（排在佇列前面的人）則根本不用付費。此外，已經將擁堵外部性納入決策過程中的是後續者，因此對他們徵收通行費相當於對他們徵收兩次費用，與對領先者徵收通行費形成對比。鑑於對任何一方徵收費用都可以消除外部性，對延誤者而不是被延誤者徵收費用將更合理，這與環保主義者提倡的“汙染者付費原則”非常類似。這也更公平，因為現在所有旅行者的總成本（擁堵延誤+通行費）將趨於一致。這樣做的缺點是，在第一個旅行者透過時，造成的延誤量是未知的，最多隻能估計。

隱含地，這優先考慮了“暢通無阻的旅行權利”而不是“免費旅行權利”。這是一個哲學問題，但考慮到需要某種機制來資助公路，我們可以完全消除免費旅行的概念，剩下的問題是如何實施融資：採用像燃油稅或固定通行費這樣的不敏感價格，還是採用與時間相關（或與流量相關）的擁堵價格。

邊際成本等於邊際延誤公式忽略了時間表延誤問題。在邊際成本價格中不包含時間表延誤有實際原因。與延誤不同，時間表延誤不容易衡量。雖然道路管理人員可以根據交通流量告訴你某個旅行者造成了多少延誤，但管理人員並不知道造成了多少時間表延誤。其次，如果遲到（早到）的懲罰很大，那麼它將主導排程。旅行者可以決定他們寧願忍受提前到達（沒有延誤）還是準時到達，並承受一定的延誤（或兩者兼而有之），從而儘可能地將相關成本降到最低。如果他們選擇延誤，那麼延誤是成本更低的替代方案。他們所遭受的較低成本就是他們所遭受的成本，因此可以作為歸因於其他旅行者的邊際成本的下限。如果他們選擇時間表延誤（這將成為他們面臨的成本）並避免延誤，他們也會受到其他旅行者的影響，但這種影響對定價機構來說是未知的。他們被“排擠出市場”，這種事情經常發生。簡而言之，將時間表延誤內生化是件好事，但這需要比實際可用資訊更多資訊。

利潤最大化定價

一個現實的公路網路在經濟學家的術語中並非完全競爭的。由於一條公路佔據了獨一無二的空間，它獲得了某種程度的壟斷力量。雖然在大多數情況下使用者可以切換到其他路線和線路，但這些替代方案對使用者的旅行時間成本更高。理論表明，超額利潤會吸引新進入者進入市場，但建造一條新公路的成本很高，這表明進入壁壘難以克服。

雖然公路通常被視為公共產品，但在擁堵時它們是競爭性的，並且在許多情況下是可排除的。這表明將它們私有化是可行的。私有化帶來的優勢很多：透過公路定價提高交通系統的效率，為設施運營商提供透過創新和創業精神改進服務的激勵，以及減少基礎設施建設和擴建的時間和成本。

一個很少被提及的問題是實施。大多數公路定價試驗假設要麼是對單一設施徵收通行費，要麼是區域控制。理論研究通常假設對路段實施邊際成本定價，並沒有討論所有權結構。然而，在經濟的其他部門，無論是透過政府所有制還是監管，對價格的中央控制已被證明不如分散控制在快速變化的環境中滿足客戶需求方面有效。全系統範圍內統一的價格系統無法提供像特定路段價格那樣的資訊。僅以邊際成本定價的路段，是最佳環境下完全競爭的最佳解決方案，會限制利潤。雖然短期內超額利潤在社會上並非最優，但從長期來看，它會吸引資本和企業家進入該經濟部門。新的資本將更多地投資於現有技術，以便進一步部署它，並以競爭者的身份進入該部門，試圖從空間壟斷或寡頭壟斷中獲益。此外，新的資本家也可能會進行創新，從而改變該行業的供求曲線。

透過從分散的角度考察公路定價和私有化，可以更全面地探討與公路市場相關的各種問題，包括短期和長期分配後果以及整體社會福利。本研究的主要貢獻將是，從理論和概念層面以及透過進行模擬實驗來解決這個問題。該分析將確定決定系統性能的顯著經驗因素和關鍵引數。在可獲得近期公路定價實驗的資料的情況下，可以將其用於與模型結果進行比較。

案例 1. 簡單壟斷

最簡單的例子是壟斷路段 $I-J$

該路段具有彈性需求 $Q_{d}$

$Q_{d}=f(P)$

這裡用線性方程給出

$Q_{d}=\beta _{0}-\beta _{1}P$ 對於所有 $\beta _{0}$ 和 $\beta _{1}>0$  

該連結的目標是最大化利潤 $\pi =PQ_{d}(P)$。 我們假設沒有擁堵效應。 利潤在當一階導數等於零且二階導數為負時被最大化。 $\pi =PQ_{d}(P)=P(\beta _{0}-\beta _{1}P)=\beta _{0}P-\beta _{1}P^{2}$ 給出以下一階條件 (f.o.c.)： $\delta \pi /dP=\beta _{0}-2\beta _{1}P=0$

$P=\beta _{0}/2\beta _{1}$

檢查二階條件 (s.o.c.)，我們發現它們小於零，正如最大值所要求的那樣。

$\delta ^{2}\pi /\delta P^{2}=-2\beta _{1}<0$

對於這個例子，如果 $\beta _{0}=1000$ 且 $\beta _{1}=1$，$P=500$ 給出 $Q_{d}(P)=500$，且 $profit=250,000$。 這種情況顯然沒有最大化社會福利，社會福利定義為利潤和消費者剩餘之和。 在 $P=500$ 的情況下，該需求曲線的消費者剩餘為 125,000，從而產生 375,000 的社會福利 (SW)。 社會福利的潛在最大值在 $P=0$ （當連結沒有成本時）將是 $500,000>375,000$，所有這些都來自消費者剩餘。

案例 2. 壟斷完全互補

在第二個簡單的例子中，我們想象兩個獨立的連結，$I-J$ 和 $J-K$，它們是純粹的壟斷和完全的互補，一個不能被消費而另一個也不能被消費（駕駛）。這些連結是串聯的。

在這種情況下，需求取決於兩個連結的價格，因此我們可以使用以下一般表示式和線性示例來進行說明：$Q_{d}=f(P_{ij},P_{kl})$

$Q_{d}=\beta _{0}-\beta _{1}(P_{ij}+P_{jk})$

我們再次假設沒有擁塞成本。當我們利潤最大化時，我們得到一個系統，它產生了一個納什均衡，該均衡對於鏈路所有者來說更糟糕，他們面臨著更低的利潤，對於鏈路使用者來說也更糟糕，他們面臨著更高的集體利潤，而不是壟斷。簡而言之，鏈路不會像在壟斷情況下那樣遭受其自身定價策略的全部影響，在壟斷情況下，定價外部性被內化了。

$\pi _{ij}=P_{ij}Q_{d}(P)=P_{ij}(\beta _{0}-\beta _{1}P_{ij}-\beta _{1}P_{jk})=\beta _{0}P_{ij}-\beta _{1}P_{ij}^{2}-\beta _{1}P_{ij}P_{jk}$

$\pi _{jk}=P_{jk}Q_{d}(P)=P_{jk}(\beta _{0}-\beta _{1}P_{ij}-\beta _{1}P_{jk})=\beta _{0}P_{jk}-\beta _{1}P_{jk}^{2}-\beta _{1}P_{ij}P_{jk}$

f.o.c. $\delta \pi /dP_{ij}=\beta _{0}-2\beta _{1}P_{ij}-\beta _{1}P_{jk}=0$

$P_{ij}=(\beta _{0}-\beta _{1}P_{jk})/2\beta _{1}$

$\delta \pi /\delta P_{jk}=\beta _{0}-2\beta _{1}P_{jk}-\beta _{1}P_{ij}=0$

$P_{jk}=(\beta _{0}-\beta _{1}P_{ij})/2\beta _{1}$

同時求解f.o.c.得到

$P_{ij}=P_{jk}=\beta _{0}(2\beta _{1}-1)/(4\beta _{1}^{2}-\beta _{1})$

檢查s.o.c.: $\delta ^{2}\pi /\delta P_{ij}^{2}=-2\beta _{1}<0$

$\delta ^{2}\pi /\delta P_{jk}^{2}=-2\beta _{1}<0$

當 $\beta _{0}=1000$ 且 $\beta _{1}=1$ 時，解為 $P_{ij}=P_{jk}=333.33$，這將導致 $Q_{d}(P)=333.33$，$\pi _{ij}=\pi _{jk}=111,111$，這比簡單壟斷情況下的總利潤要低。這種情況導致兩家公司的總利潤為222,222，消費者剩餘為55,555，社會福利總額為277,000，這低於簡單壟斷情況下的結果。類似的論證也適用於三個（或更多）完全互補的產品，如果獨立運營，它們將變得越來越不可行。 對於具有線性需求和 $\beta _{1}=1$ 的 N 個獨立的完全互補鏈路，其一般公式為

$P=Q_{d}(P)=\beta _{0}/(N+1).$

案例 3. 完全替代品的雙寡頭壟斷

在第三個例子中，我們假設有兩個平行的獨立鏈路，$I-J$ 和 $K-L$，它們服務於同一個同質市場。  它們是完全替代品（平行運營）。

此案例的最佳定價取決於對使用者如何在供應商之間分配以及鏈路之間關係的假設。 首先，假設不存在擁塞成本，並且時間成本在其他方面是相等的，並且不是決策中的因素。 使用者是否簡單地確定性地選擇最低成本的鏈路，或者是否有其他因素影響了這種選擇，從而導致價格的微小降低不會吸引所有使用者從另一條鏈路轉移？ 在這個例子中，我們假設確定性路線選擇，因此需求選擇最低成本的鏈路，或者在鏈路釋出相同價格的情況下在鏈路之間分配。 這裡，需求定義如下

$Q_{d}=f(P_{ij},P_{kl})$

$Q_{d}=\beta _{0}-\beta _{1}min(P_{ij},P_{kl}).$

與之前一樣，令 $\beta _{0}=1000$，$\beta _{1}=1$。  也假設競爭性連結可以立即做出響應。  假設每個連結可以服務整個市場，因此不存在容量限制。很明顯，存在一個（福利最大化）穩定均衡點，即 $P=0$（假設連結的成本相同且為零），這是競爭體系的結果。  證明：假設每個連結設定價格為 500，擁有 250 個使用者。  如果連結 IJ 將其價格降低一個單位至 499，它將獲得所有 501 個使用者，而 IJ 連結的利潤將從 125,000 增加至 249,999。  但是，KL 連結的利潤將降至 0。  KL 的最有利可圖的決策是將其價格降低至 498，獲得 502 個使用者，並獲得 249,996 的利潤。  這種價格戰可以持續下去，直到利潤被消除。  在該過程中的任何時刻，一個連結獨自提高價格都會導致其失去所有需求。

但是，在只有兩個連結的情況下，這種情況似乎不太可能發生。  因此，如果連結能夠協調其行動，他們會希望這樣做。  即使沒有正式的卡特爾，戰略博弈和各種價格訊號方法也是可能的。    例如，具有遠見的連結 KL 看到價格戰最終會損害兩家公司，因此它可能只會匹配降價，而不是反擊時進行降價。  如果 IJ 沒有跟隨降價，那麼價格就會維持。  有人認為（Chamberlin 1933），雙頭壟斷將像壟斷一樣運作，兩個連結將收取壟斷價格並將需求平均分配，因為這是每個連結的最佳結果，因為降價會導致價格戰，其中一個連結要麼匹配要麼降價另一個連結，這兩種情況下都會導致利潤減少。

情況 4. 壟斷與擁堵

前三種情況沒有利用交通系統的任何特殊特徵。  在本例中，在情況 1 中使用的網路上引入了旅行時間。  這裡，需求是價格 ($P$) 和時間 ($T$) 的函式。

$Q_{d}=f(P,T)$

對於本例，它由線性形式給出

$Q_{d}=\beta _{0}-\beta _{1}P-\beta _{2}T$

其中，旅行時間透過以下表達式進行評估，該表示式包含距離效應和擁堵（在一定時間內，在固定時間段內，穩定的需求導致瓶頸處的排隊）。

如果 $(Q_{d}/Q_{o})<1$

$T=T_{f}$

如果 $(Q_{d}/Q_{o})\geq 1$

$T=T_{f}+(C/2)((Q_{d}/Q_{o})-1)$

其中：$T_{f}$ = 自由流旅行時間，$C$ = 擁堵期長度，$Q_{o}$ = 透過瓶頸的最大流量。

因為 $T_{f}$ 是一個常數，並且我們只處理單個連結，它可以與 $\beta _{0}$ 組合用於分析，不會進一步考慮。 觀察可知，如果 $Q_{o}$ 很大，它也不會出現在分析中。 從情況 1 可以看出，當 $\beta$ 給定後，$Q_{o}$ 只有在小於 $Q_{d}=500$ 時才重要。 因此，對於此示例，我們將設定 $Q_{o}$ 為小於 500 的值，在本例中，假設 $Q_{o}=250$.

與之前一樣，連結的目標是最大化利潤 $\pi =PQ_{d}(P)$。當一階導數設為零且二階導數為負時，利潤最大化。

$\pi =PQ_{d}(P)=P(\beta _{0}-\beta _{1}P-\beta _{2}T)=\beta _{0}P-\beta _{1}P^{2}-\beta _{2}P(C/2)((Q_{d}/Q_{o})-1)$

給出以下一階條件 (f.o.c.)

$\delta \pi /dP=\beta _{0}-2\beta _{1}P-\beta _{2}(C/2)((Q_{d}/Q_{o})-1)=0$

$P=(\beta _{0}-\beta _{2}(C/2)((Q_{d}/Q_{o})-1))/(2\beta _{1})$

聯立求解方程 (4.2) 和 (4.6)，在以下值時：$\beta _{0}=1000$，$\beta _{1}=\beta _{2}=1$，反映了在所選單位集中，所有同質旅行者的旅行時間為 1， $C=1800$，表示 1800 個時間單位（如秒）的擁堵，我們得到以下答案：$P=Q_{d}=339.3,T=320.4$。  因此，在短期內，當產能固定時，壟斷企業有利於允許擁堵（延誤）繼續存在，而不是將價格提高到足以完全消除擁堵的程度。 從長遠來看，產能擴張（減少延誤）將使壟斷企業能夠收取更高的價格。 在這種情況下，$\pi =115,600$，並且$consumersurplus=57,800$。 與案例 1 相比，擁堵造成的無謂損失很大。

模擬

更復雜的網路不容易用上述方式進行分析。 道路在同一時間既是互補品又是替代品。 模擬模型針對更復雜的網路，回答了分析模型中提出的相同問題，即在不同的模型引數和場景下，效能指標和市場組織是什麼。 其次，我們可以考慮模型框架內的市場組織，因此問題變成：在不同的假設下，會形成什麼樣的市場組織，這種組織的社會福利後果是什麼？

競爭道路限制了自主道路所能收取的能夠最大化利潤的價格。 此外，政府法規可能會最終限制價格，儘管法規的水平可能為所有者提供很大的自由度。 預計每條道路都會有一個利潤最大化的目標函式。  然而，根據企業是否完全瞭解市場需求以及企業如何看待競爭對手行動的假設，問題的納什均衡解可能不是唯一的，甚至可能不存在。

由於一條道路上的需求取決於上游和下游道路（其互補品）的價格，因此，互補道路之間的收益分成以及隨之而來的價格協調，可能更好地服務於所有道路，增加它們的利潤並提高社會福利。高度互補道路之間的垂直整合是帕累託效率的。

人們普遍認識到，公路網路至少在一定程度上受密度經濟的影響。 這意味著，在其他條件相同的情況下，隨著一條道路上的交通流量增加，該道路的平均運營成本會下降。  至於道路是否受規模經濟的影響，即建設和管理兩條道路、更長道路或更寬道路的每單位產出（例如，每乘客公里行駛里程）的成本是否比建設和管理單條道路、更短道路或更窄道路的成本更低，這一點尚不清楚。  如果有這樣的規模經濟，則道路成本函式應該反映這一點。

不同類別使用者（富人或窮人；或汽車、公共汽車或卡車）對時間的價值不同。 在一條道路上花費的時間取決於該道路上的流量，而流量又取決於價格。 因此，對於某些道路來說，將價格定高並服務於對時間價值較高的較少使用者，而另一些道路則將價格定低並服務於對時間價值較低的更多使用者，可能是一種可行的策略。 據推測，在一個足夠複雜的網路中，這樣的不同定價策略應該從簡單的利潤最大化規則和有限的協調中產生。

在這樣的模擬模型中，需要考慮許多引數和規則，以下列出一些引數和規則。 

引數

網路規模和形狀。 必須考慮的第一個問題是網路的規模，即道路和節點的數量，以及這些道路如何連線，由網路的形狀決定（對稱：網格狀、輻射狀； 非對稱）。 雖然研究將從一個小規模網路開始，但有限網路上發現的均衡條件可能不會在更復雜的網路上出現，因此有必要考慮更現實的系統。

需求規模和形狀。 第二個問題是網路服務的起源-目的地市場的數量、需求水平以及使用者類別的數量（每個類別都有不同的時間價值）。 同樣，雖然研究將從非常簡單的假設開始，但在簡單條件下的結果可能與在略微複雜的情況下下的結果截然不同。

規則

利潤追求。 在動態情況下，自主道路如何確定能夠最大化利潤的價格？  每條自主道路決策的背後，是一個目標函式，即在一定資訊量下，利潤最大化，以及一個行為規則，該規則規定了根據某些因素，價格變化的數量和方向。 一旦一條道路找到了一種既不能提高也不能降低而不會損失利潤的收費標準，它就會傾向於堅持下去。然而，更明智的道路可能會意識到，雖然它可能已經找到了一個區域性最大值，但由於構成複雜網路的非線性，它可能沒有達到全域性最大值。 此外，其他道路可能不會像這樣堅定地堅持自己的決策，因此有必要透過測試替代價格來定期探查市場格局。 這也需要規則。

收益分成。 互補道路之間形成聯盟以協調行動，以最大化利潤，這可能是有利的。 這些聯盟是如何形成的？ 透過將其他道路的一部分利潤納入一條道路的目標函式，這條道路可以更合理地定價。在 0 到 100% 之間，哪種比例的收益分成最好？ 這些問題需要用模型進行測試。 需要開發一個道路間談判流程。

成本分攤。與收益分成類似的是，分攤每條道路面臨的某些費用。 道路會定期面臨鉅額支出，例如重新鋪設路面或冬季清雪，這些支出具有規模經濟效益。 這些規模經濟效益可以透過對大量道路的單一所有權或透過形成經濟網路來實現。 正如道路之間的收益分成是一個可以協商的變數，成本分攤也是如此。

規則評估和傳播。 最後要考慮的一組問題是規則之間競爭的可能性。 如果我們認為規則與擁有道路或道路股份並制定定價政策的企業相關聯，那麼這些規則就可以競爭。 積累的利潤可以被更成功的規則用來從不太成功的規則手中購買股份。 出售的決定將比較當前管理下的未來預期利潤與競爭企業支付的總額。 需要對道路股份的公開市場進行建模，以測試這些問題。 同樣，也可以對能夠學習並迭代獲得更多智慧的規則進行建模。

討論

正如航空網路似乎已經演變為樞紐和輻條的層次結構一樣，私人公路網路中可能存在一種最佳幾何形狀。 初步分析表明，高度互補道路的垂直整合對私人和社會福利都有好處。 然而，整合對公共和私人利益都有利的互補程度還有待確定。 其他需要研究的問題包括替代品的影響以及透過需求交叉彈性、基礎設施供應的規模經濟、具有不同時間價值的多種使用者類別、“免費”道路與收費道路的競爭以及監管約束的影響對定價政策的影響。 利用分析方法中提出的原則，將開發一個自主道路透過自適應預期學習系統行為的重複道路定價博弈。

其他問題

• 作業

參考文獻

• Chamberlin, E (1933) "壟斷競爭". 哈佛大學出版社
• 科斯，羅納德（1992），"社會成本問題，以及社會成本問題的一些註解"，轉載自公司、市場與法律，芝加哥：芝加哥大學出版社。
• Daganzo，Carlos。（1995）。交通流理論的非正式介紹。加州大學伯克利分校交通研究中心。加州伯克利。
• Levinson，David 和 Peter Rafferty（2004）延誤付費原則：檢驗帶補償的擁堵定價。國際交通經濟學雜誌 31:3 295-311
• 維克裡，威廉（1969）擁堵理論與交通投資。美國經濟評論 59，第 251-260 頁。