交通基礎/路線選擇

路線分配、路線選擇或交通分配涉及在交通網路中選擇起點和目的地之間的路線（稱為路徑）。它是傳統的交通預測模型中的第四步，緊隨出行生成、目的地選擇和出行方式選擇。出行分配的區域間互動分析提供了起點-目的地出行表。出行方式選擇分析表明哪些出行者將使用哪種出行方式。為了確定設施需求以及成本效益，我們需要知道網路中每條路線和每條鏈路上的出行者數量（路線只是起點和目的地之間的一系列鏈路）。我們需要進行交通（或出行）分配。假設有一個公路和公共交通系統網路，以及一個擬議中的擴建專案。我們首先需要知道當前的出行時間和出行流量模式，然後是如果擴建專案完成會發生什麼。

鏈路效能函式

駕駛員給其他人帶來的成本被稱為邊際成本。然而，在做決定時，駕駛員只面對自己的成本（平均成本），而忽略了給其他人帶來的任何成本（邊際成本）。

$AverageCost=S_{T}/Q$
$MarginalCost=\delta S_{T}/\delta Q$

其中 $S_{T}$ 是總成本， $Q$ 是流量。

BPR鏈路效能函式

假設我們正在考慮一個公路網路。對於每條鏈路，都存在一個函式表明阻力與交通流量之間的關係。美國公共道路局 (BPR) 開發了一個鏈路（弧）擁塞（或流量-延遲，或鏈路效能）函式，我們將其稱為S_a(Q_a)

$S_{a}\left({Q_{a}}\right)=t_{a}\left({1+0.15\left({\frac {Q_{a}}{c_{a}}}\right)^{4}}\right)\,\!$

t_a = 鏈路 a 的自由流出行時間，單位為時間

Q_a = 鏈路 a 上的交通流量（或體積），單位為時間（更準確地說：嘗試使用鏈路 a 的流量）

c_a = 鏈路 a 的容量，單位為時間

S_a(Q_a) 是車輛在鏈路 a 上的平均出行時間

還有其他擁塞函式。CATS 長期使用與 BPR 不同的函式，但當比較 CATS 和 BPR 函式時，結果似乎沒有太大差異。

流量可以超過容量嗎？

在一條鏈路上，容量被認為是“流出”。需求是流入。

如果一段時間內流入 > 流出，就會出現排隊（以及延誤）。

例如，在 1 小時內，如果 2100 輛車到達，2000 輛車離開，那麼還有 100 輛車仍在鏈路上。鏈路效能函式試圖以一種簡單的方式來表示這種現象。

沃德羅普的均衡原理

使用者均衡

每個使用者都採取行動來最小化自己的成本，前提是其他所有使用者也這樣做。所有使用路線的出行時間相同，並且低於任何未使用的路線的出行時間。

系統最優

每個使用者都採取行動來最小化系統上的總出行時間。

無政府狀態的價格

我們之所以出現擁塞，是因為人們是自私的。這種自私的成本（當人們根據自己的利益而不是社會的利益行事時）就是無政府狀態的價格。

使用者均衡條件下系統範圍內的出行時間與系統最優條件下系統範圍內的出行時間的比率。

無政府狀態的價格 = $UE/SO>1$

對於具有線性鏈路效能函式（延遲函式）的雙鏈路網路，無政府狀態的價格小於4/3。

這是否過高？是否應該採取措施，或者33%的浪費是可以接受的？ [在其他情況下，在不同的假設下，損失可能更大/更小，等等。]

流量守恆

道路分配中一個重要的因素是流量守恆。這意味著在給定的時間段內，進入交叉路口（鏈路段）的車輛數量等於離開交叉路口的車輛數量（源點和匯點除外）。

類似地，進入鏈路後部的車輛數量等於離開前部的車輛數量（在很長一段時間內）。

自動分配

長期技術

以上示例適用於雙鏈路問題，但實際網路要複雜得多。估計每條路線上的使用者數量問題由來已久。隨著高速公路和快速路（高速公路）的建設，規劃者開始對此問題進行深入研究。高速公路比當地街道系統提供更優良的服務水平，並將交通從當地系統中轉移出去。最初，轉移是主要的技術。使用出行時間的比率，並輔以成本、舒適度和服務水平的考慮。

芝加哥地區交通研究 (CATS) 的研究人員開發了高速公路與當地街道的轉移曲線。加州也做了很多工作，因為加州在高速公路規劃方面有早期經驗。除了轉移型別的研究之外，CATS 還針對在處理複雜網路時出現的一些技術問題進行了研究。其中一項成果是用於查詢網路上最短路徑的摩爾演算法。

轉移方法無法處理的問題是鏈路和路線上的交通量對出行時間的影響。如果大量車輛試圖使用某項設施，該設施就會變得擁擠，出行時間就會增加。在沒有考慮反饋機制的情況下，早期的規劃研究（實際上，大多數研究是在 1960 年至 1975 年期間）忽略了反饋。他們使用摩爾演算法確定最短路徑，並將所有交通分配到最短路徑。這就是所謂的全或無分配，因為從 i 到 j 的所有交通都沿著某條路線行駛，或者根本不行駛。

從技術計算的角度來看，全或無或最短路徑分配並非微不足道。每個交通區域都連線到 n-1 個區域，因此需要考慮許多路徑。此外，我們最終關注的是鏈路上的交通流量。一條鏈路可能是幾條路徑的一部分，並且需要將沿著路徑的交通流量逐鏈路相加。

可以提出一個支援全或無方法的論點。該論點如下：規劃研究旨在支援投資，以便所有鏈路都提供良好的服務水平。使用與計劃的服務水平相關的出行時間，計算結果表明改進到位後交通將如何流動。瞭解鏈路上的交通流量，就可以計算出滿足所需服務水平所需的容量。

啟發式程式

為了考慮交通負荷對出行時間和交通均衡的影響，開發了若干啟發式計算程式。一種啟發式方法按增量進行。要分配的交通量被分成幾部分（通常為 4 部分）。分配第一部分交通量。計算新的出行時間，然後分配下一部分交通量。重複最後一步，直到分配完所有交通量。CATS 使用了該方法的變體；它按行分配 OD 表中的資料。

FHWA 收集的計算機程式中包含的啟發式方法採用另一種方式。

步驟 0：首先使用全或無程式載入所有交通流量。
步驟 1：計算由此產生的出行時間，然後重新分配交通流量。
步驟 2：現在，開始使用權重進行重新分配。計算前兩次載入中的加權出行時間，並將其用於下一次分配。最新的迭代獲得 0.25 的權重，之前的迭代獲得 0.75 的權重。
步驟 3. 繼續進行。

這些程式似乎“執行良好”，但並不精確。

弗蘭克-沃爾夫演算法

Dafermos（1968）應用了弗蘭克-沃爾夫演算法（1956 年，Florian 1976），該演算法可用於處理交通均衡問題。

均衡分配

為了將交通流量分配到路徑和鏈路，我們必須制定規則，並且存在著名的沃德羅普均衡（1952 年）條件。這些條件的實質是，旅行者會努力尋找從起點到終點的最短（阻力最小）路徑，並且當沒有旅行者可以透過切換到新路徑來減少出行努力時，就會發生網路均衡。這些被稱為使用者最優條件，因為一旦系統處於均衡狀態，任何使用者都不會從更改出行路徑中獲益。

使用者最優均衡可以透過解決以下非線性規劃問題來找到

$\min \sum _{a}{\int _{0}^{v_{a}}{S_{a}\left(Q_{a}\right)}}dx\,\!$

受制於

$Q_{a}=\sum _{i}{\sum _{j}{\sum _{r}{\alpha _{ij}^{ar}Q_{ij}^{r}}}}\,\!$

$\sum _{r}{Q_{ij}^{r}=Q_{ij}}\,\!$

$Q_{a}\geq 0,\;Q_{ij}^{r}\geq 0\,\!$

其中 $Q_{ij}^{r}\,\!$ 是從起點 i 到終點 j 的路徑 r 上的車輛數量。因此，約束 (2) 表明所有旅行必須發生：i = 1 ... n; j = 1 ... n

$\alpha _{ij}^{ar}\,\!$ = 1 當且僅當連結 a 在從 i 到 j 的路徑 r 上；否則為零。

因此，約束 (1) 對每個連結上的流量求和。網路上的每個連結都有一個約束。約束 (3) 確保沒有負流量。

公共交通分配

也有一些方法被開發用來將乘客分配到公共交通工具。^[1]為了提高公共交通分配估計的準確性，通常會做出一些假設。這些假設的示例包括以下內容

所有公共交通出行都按照既定且預先定義的時間表執行，該時間表是已知的或對使用者容易獲得的。
公共交通服務（汽車/有軌電車/公交車容量）具有固定容量。^[2]

示例

示例 1

T問題

問題

如果連結 a 上的連結效能函式

$S_{a}=5+2*Q_{a}\,\!$

而連結 b 上的函式

$S_{b}=10+Q_{b}\,\!$

其中起點和終點之間的總流量為 1000 次旅行。求解兩條並聯連結的簡單網路中連結 a 和 b 上的流量。

示例

解決方案

時間（成本）在所有使用過的路線中都相等，因此 $S_{a}=S_{b}$

我們還有流量守恆，因此 $Q_{a}+Q_{b}=Qo=Qd=1000$

$5+2*(1000-Q_{b})=10+Q_{b}$

$1995=3Q_{b}$

$Q_{b}=665;Q_{a}=335$

示例 2

T問題

問題

Eash、Janson 和 Boyce（1979 年）的一個示例將說明非線性規劃問題的解決方案。從節點 1 到節點 2 有兩條連結，每條連結都有一個阻力函式（參見圖 1）。圖 2 中曲線下的區域對應於公式 1 中從 0 到 a 的積分，它們加起來等於 220,674。請注意，連結 b 的函式是反方向繪製的。

$S_{a}=15\left({1+0.15\left({\frac {Q_{a}}{1000}}\right)^{4}}\right)\,\!$

$S_{b}=20\left({1+0.15\left({\frac {Q_{b}}{3000}}\right)^{4}}\right)\,\!$

$Q_{a}+Q_{b}=8000\,\!$

請用圖形顯示均衡結果。

示例

解決方案

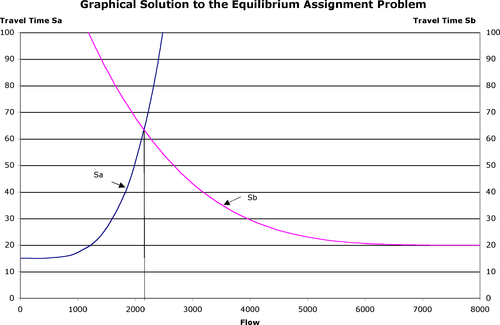
在均衡狀態下，路線 *a* 上有 2152 輛車，路線 *b* 上有 5847 輛車。每條路線的旅行時間相同：大約 63 分鐘。

圖 3 說明了與均衡解不一致的車輛分配。曲線保持不變，但隨著車輛在路線上的重新分配，陰影區域必須包含在解中，因此圖 3 中的解比圖 2 中的解大陰影區域的面積。

例 3

T問題

問題

Assume the traffic flow from Milwaukee to Chicago, is 15000 vehicles per hour. The flow is divided between two parallel facilities, a freeway and an arterial. Flow on the freeway is denoted  $Q_{f}$ , and flow on the two-lane arterial is denoted  $Q_{a}$ .

高速公路的旅行時間（以分鐘計）（ $C_{f}$ ) 由下式給出

$C_{f}=10+Q_{f}/1500\,\!$

幹線的旅行時間（ $C_{a}$ ) 由下式給出

$C_{a}=15+Q_{a}/1000\,\!$

應用沃德羅普的使用者均衡原理，確定兩條路線的流量和旅行時間。

示例

解決方案

旅行時間彼此相等

$C_{f}=C_{a}$

$10+Q_{f}/1500=15+Q_{a}/1000$

總交通流量等於 15000

$Q_{f}+Q_{a}=15000$

$Q_{a}=15000-Q_{f}$

$10+Q_{f}/1500=15+(15000-Q_{f})/1000$

求解 $Q_{f}$

$Q_{f}=60000/5=12000$

$Q_{a}=15000-Q_{f}=3000$

$C_{f}=18$

$C_{a}=18$

思考題

我們如何讓駕駛員考慮他們的邊際成本？
或者：我們如何讓駕駛員以“系統最優”的方式行事？

示例問題

問題 (解答)
問題 (解答)

變數

$C_{T}$ - 總成本
$C_{k}$ - 路段 $k$ 的旅行成本
$Q_{k}$ - 路段 $k$ 的流量（體積）

縮略語

VDF - 交通量延遲函式
LPF - 路段效能函式
BPR - 公路局
UE - 使用者均衡
SO - 系統最優
DTA - 動態交通分配
DUE - 確定性使用者均衡
SUE - 隨機使用者均衡
AC - 平均成本
MC - 邊際成本

關鍵詞

路線分配，路線選擇，汽車分配
交通量延遲函式，路段效能函式
使用者均衡
系統最優
流量守恆
平均成本
邊際成本

外部練習

使用 STREET 網站上的 ADAM 軟體，嘗試 Assignment #3，瞭解網路特徵的變化如何影響路線選擇。

其他問題

影片

參考文獻

Dafermos, Stella. C. 和 F.T. Sparrow “一般網路的交通分配問題”。國家標準局研究雜誌，73B，第 91-118 頁。 1969 年。
Florian, Michael 編輯，交通均衡方法，施普林格出版社，1976 年。
Wardrop, J. C. “道路交通研究的某些理論方面”。土木工程師學會會刊第二部分，9，第 325-378 頁。 1952 年
Eash, Ronald, Bruce N. Janson 和 David Boyce 均衡出行分配：實際應用的優勢和意義，交通研究記錄 728，第 1-8 頁，1979 年。
Evans, Suzanne P. . “結合出行分配和路徑分配的某些模型的推導和分析”。交通研究，第 10 卷，第 37-57 頁，1976 年
Hendrickson, C.T. 和 B.N. Janson，“幾種土木工程問題的通用網路流公式”。土木工程系統 1(4)，第 195-203 頁，1984 年

進一步閱讀

背景

[1] Spiess (1993) 基於最優策略的交通均衡分配

[2] Paolo Carraresi, Federico Malucelli, Stefano Pallottino (1995) 關於區域公共交通分配

[1]

[2]