交通運輸基礎/排隊論

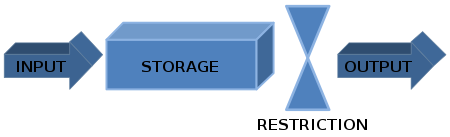
排隊系統的示意圖

排隊論研究的是在需求超過可用容量的特定路段附近的交通行為。排隊現象在許多常見情況下都能看到：乘坐公共汽車、火車或飛機，高速公路瓶頸，購物結賬，下課時離開教室門口，等待實驗室的電腦，麥當勞的漢堡包，或者理髮店的理髮。在交通工程中，排隊可能發生在紅綠燈、停車標誌、瓶頸或任何基於設計或交通的流量收縮處。如果處理不當，排隊會導致嚴重的網路擁堵或“交通堵塞”情況，因此工程師必須對其進行研究和理解。

累積輸入輸出圖（Newell曲線）

顯示排隊累積輸入和輸出的Newell曲線

基於出發率和到達率對資料，可以得到每輛車的延遲。利用圖中所示的輸入輸出 (I/O) 排隊圖，可以找到每輛車的延遲：第$i^{th}$輛車的延遲是出發時間減去到達時間（$t_{2}-t_{1}$）。總延遲是每輛車延遲的總和，也就是到達（A(t)）和離開（D(t)）曲線之間三角形的面積。

分佈

到達分佈 - 確定性（均勻）或隨機（例如泊松）

服務分佈 - 確定性或隨機

服務方式

• 先到先服務（FCFS）或先進先出（FIFO）
• 後到先服務（LCFS）或後進先出（LIFO）
• 優先順序（例如，匝道計量器上的HOV繞行）

排隊特徵

佇列長度特徵 - 有限或無限

通道數量 - 等待佇列的數量（例如，匝道=2，超市=12）

我們使用以下符號

• 到達率 = $\lambda$
• 離開率 = $\mu$

利用率 $\rho ={\frac {\lambda }{\mu }}\,\!$

飽和度

過飽和：$\lambda >\mu$

欠飽和 $\lambda <\mu$

飽和 $\lambda =\mu$

Little公式

交通佇列

Little 公式: $E(n)=\lambda E(v)$

這意味著平均佇列長度（以車輛為單位）等於到達率（每單位時間車輛數）乘以平均等待時間（包括排隊延遲時間和服務時間）（以時間單位計）。該結果與特定的到達分佈無關，雖然可能很明顯，但這是一個重要的基本原理，直到 1961 年才被證明。

更多應用請參閱維基百科文章。

無容量約束佇列 (M/D/1) 和 (M/M/1)

隨機排隊佇列長度.png

隨機排隊和確定性排隊以及 BPR 的比較。

隨機排隊與 BPR 和 Akcelik 公式的比較。

已經表明，M/D/1 和 M/M/1 排隊的佇列長度、等待時間和延遲不同。這些差異體現在公式中，並在下面顯示。請注意兩者之間的細微差異。

M/D/1 和 M/M/1 佇列屬性的比較

	M/D/1	M/M/1
E(w)（平均等待時間）	$E(w)={\frac {\rho }{2\mu \left({1-\rho }\right)}}\,\!$	$E(w)={\frac {\lambda }{\mu \left({\mu -\lambda }\right)}}\,\!$
E(v)（平均總延遲）	$E(v)={\frac {2-\rho }{2\mu \left({1-\rho }\right)}}\,\!$	$E(v)={\frac {1}{\left({\mu -\lambda }\right)}}\,\!$
E(n)（系統中單位（包括正在服務的車輛）的預期數量）	$E(n)={\frac {(2-\rho )\rho }{2(1-\rho )}}\,\!$	$E(n)={\frac {\rho }{1-\rho }}\,\!$

註釋

• 平均等待時間 (E(w)) 不包括服務時間。
• 平均總延遲 (E(v)) 為（等待時間 + 服務時間）。由於瓶頸的存在，有時也將其稱為平均延遲時間。
• 系統中單位的預期數量 (E(n)) 包括當前正在服務的客戶（以單位數計）。根據 Little 公式，這是到達率乘以在系統中花費的平均時間$E(n)=\lambda *E(v)$。
• 有時需要請求佇列中單位的預期數量 (E(m))，不包括正在服務的客戶，這需要使用不同的公式（到達率乘以平均等待時間$E(m)=\lambda *E(w)$），並且顯然會得到一個較小的數字。

無容量約束佇列 (M/M/1)（隨機到達和隨機服務）

除了之前提到的屬性外，M/M/1 排隊還有一些其他需要注意的屬性。

其他 M/M/1 佇列屬性

	M/M/1
系統中 n 個單位的機率	$P\left(n\right)=\rho ^{n}\left({1-\rho }\right)\,\!$
到達的平均等待時間，包括排隊和服務	$E\left(v\right)={\frac {1}{\left({\mu -\lambda }\right)}}\,\!$
佇列中的平均等待時間（不包括正在服務的車輛）	$E\left(w\right)={\frac {\lambda }{\mu \left({\mu -\lambda }\right)}}\,\!$
系統中單位數量的期望值（包括正在服務的車輛）	$E\left(n\right)=\lambda E(v)={\frac {\lambda }{\mu -\lambda }}\,\!$
平均排隊長度（不包括正在服務的車輛）	$E\left(m\right)=\lambda E(w)={\frac {\lambda ^{2}}{\mu \left({\mu -\lambda }\right)}}\,\!$
在系統中花費時間小於或等於t的機率	$P\left({v\leq t}\right)=1-e^{-\left({1-\rho }\right)\mu t}\,\!$
在排隊中花費時間小於或等於t的機率	$P\left({w\leq t}\right)=1-\rho e^{-\left({1-\rho }\right)\mu t}\,\!$
在排隊中花費時間超過t的機率，前提是排隊不為空	$P\left({w>t}\right|{w>0})=e^{-\left({1-\rho }\right)\mu t}\,\!$
排隊車輛數量超過N的機率	$P\left({n>N}\right)=\rho ^{N+1}\,\!$

等待時間如何隨容量利用率變化

容量受限的排隊（有限）

容量受限的排隊允許最多一定數量的車輛等待，因此與無容量限制的排隊具有不同的特性。對於單通道欠飽和有限排隊，其中系統中最大單位數量指定為$N$，並且具有隨機到達和離開($\lambda ,\mu$)，我們有

其他 M/M/1 佇列屬性

	M/M/1
系統中n個單位的機率	$P(n)={\frac {\left({1-\rho }\right)}{1-\rho ^{N+1}}}\left(\rho \right)^{n}\,\!$
系統中單位數量的期望值	$E(n)={\frac {\left(\rho \right)}{\left({1-\rho }\right)^{}}}{\frac {1-\left({N+1}\right)\left(\rho \right)^{N}+N\rho ^{N+1}}{1-\rho ^{N+1}}}\,\!$

佇列產生的現實原因

道路:

• 幾何瓶頸（車道減少、急彎、坡道）
• 事故和事件
• 交通訊號燈和交叉路口控制
• 與其他交通方式平交（鐵路道口、活動橋等）
• 收費站
• 匝道計量器
• “圍觀”效應
• 惡劣天氣

火車和公交:

• 站臺容量
• 檢票口
• 售票視窗/售票機
• 火車最小安全間隔
• 安檢點
• 火車進出站效率（軌道數量、道岔等）

航空和機場:

• 跑道
• 飛機指定最小安全跟隨距離（政府規定）
• 飛機物理最小安全跟隨距離（湍流產生等）
• 進近和離場的可用空域
• 售票櫃檯/值機手續
• 安檢點
• 行李系統
• 航站樓飛機容量
• 航站樓內部乘客容量
• 惡劣天氣

水運和海運:

• 船閘和水壩
• 港口容量
• 最小“安全”距離（由政府和物理學決定）
• 惡劣天氣

太空飛行:

• 發射能力
• 軌道飛行器之間的最小間距
• 地球上的惡劣天氣
• 不利的天體條件

示例

示例1

問題

問題

在克拉斯提漢堡店，如果顧客到達率是每分鐘1人，服務率是每45秒1人，求平均排隊人數、平均等待時間和平均總延遲時間。假設為M/M/1過程。

示例

解決方案

首先，我們將所有資料轉換為分鐘。

服務時間

${45/60}=0.75minutes\,\!$ 每位顧客。或者，您可以說服務員可以處理60/45 = 1/0.75 = 1.33位顧客/分鐘。

到達率為每分鐘1位顧客。

利用率$\rho =(60/60)/(60/45)=0.75$，這意味著服務員平均75%的時間都在忙碌。

平均排隊人數 (E(n))

$E(n)={\frac {\rho }{1-\rho }}={\frac {0.75}{(1-0.75)}}=3\,\!$

$E(n)=\lambda E(v)=1*3.00$ 利特爾公式

平均等待時間

$E(w)={\frac {\lambda }{\mu \left({\mu -\lambda }\right)}}={\frac {1}{1.33\left({1.33-1}\right)}}=2.25\,\!$

平均延遲時間

$E(v)={\frac {1}{\left({\mu -\lambda }\right)}}={\frac {1}{\left({1.33-1}\right)}}=3=E(w)+servicetime=2.25+0.75\,\!$

比較

我們可以使用M/D/1方程計算相同的結果，結果如下表所示。

M/D/1 和 M/M/1 佇列屬性的比較

	M/D/1	M/M/1
E(n)（平均排隊人數）	1.875	3
E(w)（平均等待時間）	1.125	2.25
E(v)（平均總延遲）	1.875	3

可以看出，與更隨機的情況（M/M/1，既有隨機到達又有隨機服務）相關的延遲大於較不隨機的情況（M/D/1），這是預料之中的。

示例2

問題

問題

荷馬在不到1分鐘、2分鐘或3分鐘內拿到他的漢堡包的可能性有多大？

示例

解決方案

$P\left({t\leq 1}\right)=1-e^{-\left({1-\rho }\right)\mu T}=1-e^{-\left({1-0.75}\right)1.333*1}=1-e^{-0.333}=0.283\,\!$

$P\left({t\leq 2}\right)=1-e^{-\left({1-\rho }\right)\mu T}=1-e^{-\left({1-0.75}\right)1.333*2}=1-e^{-0.667}=0.487\,\!$

$P\left({t\leq 3}\right)=1-e^{-\left({1-\rho }\right)\mu T}=1-e^{-\left({1-0.75}\right)1.333*3}=1-e^{-1}=0.631\,\!$

示例 3

問題

問題

在遇到為他做漢堡的“滿臉青春痘的少年”之前，荷馬等待超過 3 分鐘的可能性是多少？

示例

解決方案

$P\left({w\leq 3}\right)=1-\rho e^{-\left({1-\rho }\right)\mu T}=1-0.75e^{-\left({1-0.75}\right)1.333*3}\,\!$

$P\left({w>3}\right)=1-P\left({w\leq 3}\right)\,\!$

示例 4

問題

問題

荷馬前面有超過 5 個顧客的可能性有多大？

示例

解決方案

$P\left({n>5}\right)=\rho ^{N+1}=0.75^{6}=0.178\,\!$

思考題

問題

如何最小化排隊等待時間？

解決方案

插隊總是能起到作用，但這個問題將在不違反任何規則的情況下得到解答。想象一下，你出去吃飯，卻發現你最喜歡的餐廳門口排著長隊。你會怎麼辦？也許當時什麼也做不了，但下次再去這家餐廳的時候，你可能會選擇一個不同的時間。也許是更早的時間，以避免午餐或晚餐的高峰時段。在交通中也可以看到類似的決策。那些厭倦了在上班途中排隊的人可能會嘗試比高峰時段更早或（如果可能）更晚出發，以減少自己的出行時間。這通常效果不錯，直到其他所有司機都想到了同樣的辦法，並將擁堵轉移到不同的時間。

美國加州的兩名摩托車騎手正在實施車道穿梭

為了最小化道路上排隊的等待時間，一些地方允許在特定情況下進行車道過濾甚至車道穿梭。其他一些地方也曾考慮過這些措施，但沒有成功。

“有證據（Hurt，1981）表明，在多車道道路（如州際公路）上穿梭於停著或緩慢行駛的汽車之間（即車道穿梭），與留在車道內並與其他車輛一起行駛相比，可以略微降低事故發生頻率。”

示例問題

示例問題 1：收費站排隊

問題 (解答)

示例問題 2：匝道計量排隊

問題 (解答)

示例問題 3：匝道計量排隊

問題 (解答)

變數

• A(t) = λ - 到達率
• D(t) = μ - 離開率
• 1/μ - 服務時間
• ρ = λ/ μ - 利用率
• Q - 平均排隊長度，包括當前正在服務的顧客（以單位數量表示）
• w - 平均等待時間
• t - 平均延遲時間（排隊時間 + 服務時間）

關鍵詞

• 排隊論
• 累積輸入輸出圖（Newell 圖）
• 平均排隊長度
• 平均等待時間
• 系統平均總延遲時間
• 到達率，離開率
• 不飽和，飽和
• D/D/1，M/D/1，M/M/1
• 通道
• 泊松分佈
• 服務率
• 有限（有容量）佇列，無限（無容量）佇列

外部練習

本次作業旨在為學生提供機會，讓他們更好地理解兩種排隊理論：M/D/1 和 M/M/1。為了幫助計算本練習中所需的數值，提供了兩個預格式化的電子表格。雖然這些電子表格提供了計算結果，但為了參考，下面列出了公式

$WT_{q}=({\frac {C_{\lambda }^{2}+C_{\mu }^{2}}{2C_{\lambda }^{2}}})({\frac {\rho }{1-\rho }}){\frac {1}{\mu }}\,\!$

其中

• $WT_{q}\,\!$：佇列中客戶的平均延遲
• $C_{\lambda }\,\!$：到達分佈的變異係數（CV）
• $C_{\mu }\,\!$：離開分佈的變異係數
• $CV\,\!$：標準差/均值；對於泊松過程，CV = (1/SqRt (均值))，對於恆定分佈，CV = 0
• $\mu \,\!$：平均離開率
• $\lambda \,\!$：平均到達率
• $\rho \,\!$：利用率 = 到達率/服務率 $(\rho =\lambda /\mu )\,\!$

M/D/1 排隊

從明尼蘇達大學的 STREET 網站下載 M/D/1 排隊的檔案：M/D/1 佇列電子表格

使用此電子表格，針對 10 種場景中的每一種執行 5 次模擬，使用下表中列出的到達和離開資訊。換句話說，將相同的資料輸入電子表格 5 次以捕獲變化的種子，從而由於模型的敏感性而產生略微不同的答案。總共將執行 50 次模擬。

場景	1	2	3	4	5	6	7	8	9	10
到達率	0.01	0.025	0.05	0.1	0.2	0.3	0.4	0.5	0.6	0.7
服務率	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5

此外，找到所有十個場景的利用率。根據利用率和分佈變異性，使用上述方程計算所有利用率值小於 1 的場景的平均延遲。

最後，在同一延遲-利用率圖中總結從模擬和 WTq 方程獲得的平均延遲。解釋您的結果。隨著利用率的增加，平均使用者延遲如何變化？上述方程是否提供了平均延遲的令人滿意的近似值？

M/M/1 排隊

從明尼蘇達大學的 STREET 網站下載 M/M/1 排隊的檔案：M/M/1 佇列電子表格

使用此電子表格，針對 10 種場景中的每一種執行 5 次模擬，使用下表中列出的到達和離開資訊。換句話說，將相同的資料輸入電子表格 5 次以捕獲變化的種子，從而由於模型的敏感性而產生略微不同的答案。總共將執行 50 次模擬。

場景	1	2	3	4	5	6	7	8	9	10
到達率	0.01	0.025	0.05	0.1	0.2	0.3	0.4	0.5	0.6	0.7
服務率	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5

同樣，您需要為每個場景使用五個不同的隨機種子。在延遲-利用率圖中總結結果。解釋您的結果（您不需要使用上面給出的 WTq 方程來計算 M/M/1 佇列的延遲）。

其他問題

• 最後比較 M/M/1 佇列和 M/D/1 佇列。你能得出什麼結論？（對於相同的平均到達率，使用者在這兩個排隊系統中是否會遇到相同的延遲？為什麼或為什麼不？）
• 提供一個簡短的示例，說明 M/M/1 可能是在何種情況下使用合適的模型。
• 提供一個簡短的示例，說明 M/D/1 可能是在何種情況下使用合適的模型。

其他問題

• 其他問題
• 作業

影片

• 排隊論導論
• 確定性佇列
• 岩石漏斗實驗
• 隨機佇列
• 隨機佇列 - 機率分佈
• 排隊 - 收費站示例