線性代數/行列式作為大小函式

線性代數
← 行列式的幾何意義	行列式作為大小函式	行列式的其他公式 →

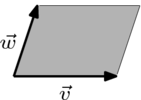
這個平行四邊形圖

是我們從兩個向量的和的構造中熟悉的。計算它所包圍的面積的一種方法是畫出這個矩形，然後減去每個子區域的面積。

${\begin{array}{l}{\text{area of parallelogram}}\\\quad ={\text{area of rectangle}}-{\text{area of }}A-{\text{area of }}B\\\qquad -\cdots -{\text{area of }}F\\\quad =(x_{1}+x_{2})(y_{1}+y_{2})-x_{2}y_{1}-x_{1}y_{1}/2\\\qquad -x_{2}y_{2}/2-x_{2}y_{2}/2-x_{1}y_{1}/2-x_{2}y_{1}\\\quad =x_{1}y_{2}-x_{2}y_{1}\end{array}}$

面積等於行列式的值

{\begin{vmatrix}x_{1}&x_{2}\\y_{1}&y_{2}\end{vmatrix}}=x_{1}y_{2}-x_{2}y_{1}

並非巧合。行列式定義中的性質為衡量矩陣中向量所包圍區域大小的函式提供了合理的假設。

例如，這顯示了將一個定義方框的向量乘以一個標量（使用的標量為 $k=1.4$ ）。

由 $k{\vec {v}}$ 和 ${\vec {w}}$ 所形成的區域比由 ${\vec {v}}$ 和 ${\vec {w}}$ 所圍成的陰影區域大 $k$ 倍。也就是說， ${\text{size}}\,(k{\vec {v}},{\vec {w}})=k\cdot {\text{size}}\,({\vec {v}},{\vec {w}})$ ，一般來說，我們期望大小度量具有 ${\text{size}}\,(\dots ,k{\vec {v}},\dots )=k\cdot {\text{size}}\,(\dots ,{\vec {v}},\dots )$ 的性質。當然，這個假設已經是我們熟知的行列式定義中的性質之一。

行列式的另一個性質是它們不受旋轉的影響。以下是旋轉前後的盒子（使用的標量是 $k=0.35$ ）。

雖然右邊的區域，由 $v$ 和 $k{\vec {v}}+{\vec {w}}$ 所形成的盒子，比陰影區域更傾斜，但它們具有相同的底邊和高度，因此面積也相同。這說明了 ${\text{size}}\,({\vec {v}},k{\vec {v}}+{\vec {w}})={\text{size}}\,({\vec {v}},{\vec {w}})$ 。推廣來說， ${\text{size}}\,(\dots ,{\vec {v}},\dots ,{\vec {w}},\dots )={\text{size}}\,(\dots ,{\vec {v}},\dots ,k{\vec {v}}+{\vec {w}},\dots )$ ，這是行列式假設的另一種說法。

當然，這張圖片

表明 ${\text{size}}\,({\vec {e}}_{1},{\vec {e}}_{2})=1$ ，我們自然地將其擴充套件到任意維數 ${\text{size}}\,({\vec {e}}_{1},\dots ,{\vec {e}}_{n})=1$ ，這是單位矩陣行列式為 1 的性質的另一種說法。

有了這一點，因為行列式的性質 (2) 是多餘的（正如在定義之後立即提到的），所以我們得出，所有行列式的性質都是對一個給出盒子大小的函式的合理預期。現在，我們可以引用上一節中所做的工作來證明行列式的存在性和唯一性，以確保這些假設是一致且充分的（我們不需要任何更多的假設）。也就是說，我們得到了一個直觀的理由來解釋 $\det({\vec {v}}_{1},\dots ,{\vec {v}}_{n})$ 作為由這些向量形成的盒子的大小。（註釋。 一種更基本的方法，它也導致下面的定義，在 (Weston 1959) 中。）

例 1.1

這個平行六面體的體積可以透過高中幾何中的通常公式求得，為 $12$ 。

${\begin{vmatrix}2&0&-1\\0&3&0\\2&1&1\end{vmatrix}}=12$

備註 1.2

雖然定義中的性質 (2) 是多餘的，但它提出了一個重要的觀點。考慮這兩個。


${\begin{vmatrix}4&1\\2&3\end{vmatrix}}=10$	${\begin{vmatrix}1&4\\3&2\end{vmatrix}}=-10$

它們之間唯一的區別是向量被取的順序。如果我們首先取 ${\vec {u}}$ ，然後轉到 ${\vec {v}}$ ，沿著所示的逆時針弧線，那麼符號為正。沿著順時針弧線會得到負號。大小函式返回的符號反映了盒子的“方向”或“意義”。（如果我們想象一個負標量乘以一個標量的效果，我們會看到同樣的事情。）

雖然方向的概念既有趣又重要，但它實際上很棘手。在下面的開發過程中不需要它，所以我們將跳過它。（見問題 20。）

定義 1.3

由 $\langle {\vec {v}}_{1},\dots ,{\vec {v}}_{n}\rangle$ (其中每個向量來自 $\mathbb {R} ^{n}$ ) 所形成的箱子（或平行六面體）包含集合 $\{t_{1}{\vec {v}}_{1}+\dots +t_{n}{\vec {v}}_{n}\,{\big |}\,t_{1},\ldots ,t_{n}\in [0..1]\}$ 的所有元素。箱子的體積是將這些向量作為列的矩陣的行列式的絕對值。

示例 1.4

體積，由於它是絕對值，因此不依賴於向量的給出順序。示例 1.1 中的平行六面體的體積也可以計算為該行列式的絕對值。

{\begin{vmatrix}0&2&-1\\3&0&0\\1&2&1\end{vmatrix}}=-12

體積的定義為空間中的某事物提供了幾何解釋，即由向量構成的箱子。下一個結果將幾何與作用於空間的函式聯絡起來。

定理 1.5

變換 $t:\mathbb {R} ^{n}\to \mathbb {R} ^{n}$ 以相同因子改變所有箱子的尺寸，即箱子 $\left|t(S)\right|$ 的影像的大小是 $\left|T\right|$ 倍的箱子 $\left|S\right|$ 的大小，其中 $T$ 是相對於標準基表示 $t$ 的矩陣。也就是說，對於所有 $n\!\times \!n$ 矩陣，乘積的行列式等於行列式的乘積 $\left|TS\right|=\left|T\right|\cdot \left|S\right|$ 。

這兩句話表達了同一個意思，第一句話用對映的術語，第二句話用矩陣的術語。雖然我們傾向於使用對映的觀點，但第二句話，矩陣的版本，在證明中更方便，也是我們以後使用該結果的方式。（備選證明見問題 16和問題 21）。

證明

這兩個表示式是等價的，因為 $\left|t(S)\right|=\left|TS\right|$ ，它們都表示單位立方體 ${\mathcal {E}}_{n}$ 在複合變換 $t\circ s$ 下的像的體積（其中 $s$ 是由 $S$ 關於標準基表示的對映）。

現在考慮這種情況， $\left|T\right|\neq 0$ ，即 $T$ 是非奇異的。回想一下，任何非奇異矩陣都可以分解成初等矩陣的乘積，因此 $TS=E_{1}E_{2}\cdots E_{r}S$ 。在接下來的論證中，我們將驗證如果 $E$ 是一個初等矩陣，則 $\left|ES\right|=\left|E\right|\cdot \left|S\right|$ 。結果將隨之而來，因為然後 $\left|TS\right|=\left|E_{1}\cdots E_{r}S\right|=\left|E_{1}\right|\cdots \left|E_{r}\right|\cdot \left|S\right|=\left|E_{1}\cdots E_{r}\right|\cdot \left|S\right|=\left|T\right|\cdot \left|S\right|$ .

如果初等矩陣 $E$ 是 $M_{i}(k)$ ，那麼 $M_{i}(k)S$ 等於 $S$ ，除了第 $i$ 行被乘以 $k$ 。那麼行列式函式的第三個性質就表明 $\left|M_{i}(k)S\right|=k\cdot \left|S\right|$ 。但 $\left|M_{i}(k)\right|=k$ ，同樣由第三個性質得出，因為 $M_{i}(k)$ 是透過將單位矩陣的第 $i$ 行乘以 $k$ 得到的，因此 $\left|ES\right|=\left|E\right|\cdot \left|S\right|$ 對 $E=M_{i}(k)$ 成立。 $E=P_{i,j}=-1$ 和 $E=C_{i,j}(k)$ 的檢驗類似。

示例 1.6

用標準基表示的對映 $t$ 的應用

{\begin{pmatrix}1&1\\-2&0\end{pmatrix}}

將使盒子的尺寸翻倍，例如從以下

${\begin{vmatrix}2&1\\1&2\end{vmatrix}}=3$

到以下

${\begin{vmatrix}3&3\\-4&-2\end{vmatrix}}=6$

推論 1.7

如果一個矩陣可逆，那麼它的逆矩陣的行列式等於其行列式的倒數 $\left|T^{-1}\right|=1/\left|T\right|$ .

證明

$1=\left|I\right|=\left|TT^{-1}\right|=\left|T\right|\cdot \left|T^{-1}\right|$

回想一下，行列式不是加法同態， $\det(A+B)$ 不一定等於 $\det(A)+\det(B)$ 。相反，上述定理說明行列式是乘法同態： $\det(AB)$ 等於 $\det(A)\cdot \det(B)$ .

練習

問題 1

求形成的區域的體積。

$\langle {\begin{pmatrix}1\\3\end{pmatrix}},{\begin{pmatrix}-1\\4\end{pmatrix}}\rangle$
$\langle {\begin{pmatrix}2\\1\\0\end{pmatrix}},{\begin{pmatrix}3\\-2\\4\end{pmatrix}},{\begin{pmatrix}8\\-3\\8\end{pmatrix}}\rangle$
$\langle {\begin{pmatrix}1\\2\\0\\1\end{pmatrix}},{\begin{pmatrix}2\\2\\2\\2\end{pmatrix}},{\begin{pmatrix}-1\\3\\0\\5\end{pmatrix}},{\begin{pmatrix}0\\1\\0\\7\end{pmatrix}}\rangle$

建議所有讀者做這道練習。

問題 2

是

{\begin{pmatrix}4\\1\\2\end{pmatrix}}

在由這三個向量形成的箱子裡？

{\begin{pmatrix}3\\3\\1\end{pmatrix}}\quad {\begin{pmatrix}2\\6\\1\end{pmatrix}}\quad {\begin{pmatrix}1\\0\\5\end{pmatrix}}

建議所有讀者做這道練習。

問題 3

求該區域的體積。

建議所有讀者做這道練習。

問題 4

假設 $\left|A\right|=3$ 。這些變換改變體積的比例是多少？

$A$
$A^{2}$
$A^{-2}$

建議所有讀者做這道練習。

問題 5

每個變換改變盒子大小的比例是多少？

${\begin{pmatrix}x\\y\end{pmatrix}}\mapsto {\begin{pmatrix}2x\\3y\end{pmatrix}}$
${\begin{pmatrix}x\\y\end{pmatrix}}\mapsto {\begin{pmatrix}3x-y\\-2x+y\end{pmatrix}}$
${\begin{pmatrix}x\\y\\z\end{pmatrix}}\mapsto {\begin{pmatrix}x-y\\x+y+z\\y-2z\end{pmatrix}}$

問題 6

在該矩陣作用下，矩形 $[2..4]\times [2..5]$ 的影像的面積是多少？

{\begin{pmatrix}2&3\\4&-1\end{pmatrix}}

問題 7

如果 $t:\mathbb {R} ^{3}\to \mathbb {R} ^{3}$ 將體積改變了 $7$ 倍，而 $s:\mathbb {R} ^{3}\to \mathbb {R} ^{3}$ 將體積改變了 $3/2$ 倍，那麼它們的複合變換將體積改變多少倍？

問題 8

盒子的定義與生成空間的定義有何區別？

建議所有讀者做這道練習。

問題 9

為什麼這張圖沒有與定理 1.5 矛盾？

	${\xrightarrow[{}]{\scriptstyle {\begin{pmatrix}2&1\\0&1\end{pmatrix}}}}$
面積為 $2$	行列式為 $2$	面積為 $5$

建議所有讀者做這道練習。

問題 10

問題 11

假設 $\left|A\right|=3$ 且 $\left|B\right|=2$ 。求 $\left|A^{2}\cdot {{B}^{\rm {trans}}}\cdot B^{-2}\cdot {{A}^{\rm {trans}}}\right|$ 。
假設 $\left|A\right|=0$ 。證明 $\left|6A^{3}+5A^{2}+2A\right|=0$ 。

建議所有讀者做這道練習。

問題 12

設 $T$ 是表示將平面向量逆時針旋轉 $\theta$ 弧度的對映（相對於標準基）的矩陣。 $T$ 將大小改變了多少倍？

建議所有讀者做這道練習。

問題 13

一個保持面積的變換 $t:\mathbb {R} ^{2}\to \mathbb {R} ^{2}$ 是否也必須保持長度？

建議所有讀者做這道練習。

問題 14

在 $\mathbb {R} ^{3}$ 中，由線性相關集所包圍的平行六面體的體積是多少？

建議所有讀者做這道練習。

問題 15

在 $\mathbb {R} ^{3}$ 中，端點為 $(1,2,1)$ 、 $(3,-1,4)$ 和 $(2,2,2)$ 的三角形的面積是多少？（面積，而不是體積。該三角形定義了一個平面——該平面上的三角形的面積是多少？）

建議所有讀者做這道練習。

問題 16

對定理 1.5 的另一種證明使用行列式函式的定義。

注意，構成 $S$ 的向量構成線性相關集當且僅當 $\left|S\right|=0$ ，並檢查結果在這種情況下是否成立。
對於 $\left|S\right|\neq 0$ 的情況，為了證明對所有變換都成立 $\left|TS\right|/\left|S\right|=\left|T\right|$ ，考慮由 $T\mapsto \left|TS\right|/\left|S\right|$ 給出的函式 $d:{\mathcal {M}}_{n\!\times \!n}\to \mathbb {R}$ 。證明 $d$ 具有行列式的第一個性質。
證明 $d$ 具有行列式函式的其餘三個性質。
由此得出結論， $\left|TS\right|=\left|T\right|\cdot \left|S\right|$ .

問題 17

給出一個非單位矩陣，該矩陣具有 ${{A}^{\rm {trans}}}=A^{-1}$ 的性質。證明如果 ${{A}^{\rm {trans}}}=A^{-1}$ ，那麼 $\left|A\right|=\pm 1$ 。反之是否成立？

問題 18

行列式的代數性質表明，從單個行中分解一個標量將使行列式乘以該標量，這表明當 $H$ 是 $3\!\times \!3$ 時， $cH$ 的行列式是 $c^{3}$ 乘以 $H$ 的行列式。用幾何方式解釋，即使用定理 1.5。

建議所有讀者做這道練習。

問題 19

如果存在一個非奇異矩陣 $P$ 使得 $H=P^{-1}GP$ （我們將在第五章研究這種關係），則稱矩陣 $H$ 和 $G$ **相似**。證明相似矩陣具有相同的行列式。

問題 20

我們通常用標準基表示 $\mathbb {R} ^{2}$ 中的向量，因此第一象限中的向量具有兩個正座標。

${\rm {Rep}}_{{\mathcal {E}}_{2}}({\vec {v}})={\begin{pmatrix}+3\\+2\end{pmatrix}}$

沿原點逆時針方向移動，我們會迴圈遍歷四個區域

\cdots \;\longrightarrow {\begin{pmatrix}+\\+\end{pmatrix}}\;\longrightarrow {\begin{pmatrix}-\\+\end{pmatrix}}\;\longrightarrow {\begin{pmatrix}-\\-\end{pmatrix}}\;\longrightarrow {\begin{pmatrix}+\\-\end{pmatrix}}\;\longrightarrow \cdots \,.

使用此基

$B=\langle {\begin{pmatrix}0\\1\end{pmatrix}},{\begin{pmatrix}-1\\0\end{pmatrix}}\rangle$

給出了相同的逆時針迴圈。我們說這兩個基具有相同的 *方向*。

為什麼它們給出相同的迴圈？
軸上單位向量的哪些其他配置給出相同的迴圈？
找到從這些（有序）基形成的矩陣的行列式。
還有哪些逆時針迴圈是可能的，以及它們相關的行列式是什麼？
在 $\mathbb {R} ^{1}$ 中會發生什麼？
在 $\mathbb {R} ^{3}$ 中會發生什麼？

關於方向的引人入勝的普通觀眾討論見 (Gardner 1990)。

問題 21

這個問題使用了可選的行列式函式存在子部分中的材料。使用行列式的排列展開公式證明定理 1.5。

建議所有讀者做這道練習。

問題 22

證明這給出了 $\mathbb {R} ^{2}$ 中過 $(x_{2},y_{2})$ 和 $(x_{3},y_{3})$ 的直線的方程。
${\begin{vmatrix}x&x_{2}&x_{3}\\y&y_{2}&y_{3}\\1&1&1\end{vmatrix}}=0$
(Peterson 1955) 證明頂點為 $(x_{1},y_{1})$ ， $(x_{2},y_{2})$ 和 $(x_{3},y_{3})$ 的三角形的面積為
${\frac {1}{2}}{\begin{vmatrix}x_{1}&x_{2}&x_{3}\\y_{1}&y_{2}&y_{3}\\1&1&1\end{vmatrix}}.$
(Bittinger 1973) 證明頂點在 $(x_{1},y_{1})$ , $(x_{2},y_{2})$ , 和 $(x_{3},y_{3})$ 的座標都是整數的三角形的面積為 $N$ 或 $N/2$ ，其中 $N$ 是一個正整數。

解決方案

參考資料

Bittinger, Marvin (proposer) (1973), "Quickie 578", Mathematics Magazine, 美國數學學會, 46 (5): 286, 296 {{citation}}: 未知引數 |month= 被忽略了 (幫助).
Gardner, Martin (1990), The New Ambidextrous Univers, W. H. Freeman and Company {{citation}}: 未知引數 |editition= 被忽略了 (幫助).
Peterson, G. M. (1955), "Area of a triangle", American Mathematical Monthly, 美國數學學會, 62 (4): 249 {{citation}}: 未知引數 |month= 被忽略了 (幫助).
Weston, J. D. (1959), "Volume in Vector Spaces", American Mathematical Monthly, 美國數學學會, 66 (7): 575–577 {{citation}}: 未知引數 |month= 被忽略了 (幫助).

線性代數
← 行列式的幾何意義	行列式作為大小函式	行列式的其他公式 →