線性代數/Gram-Schmidt 正交化

本小節為可選內容。它需要前一個小節的內容，前一個小節也是可選內容。這裡完成的工作只在第五章的最後兩個部分需要。

前一個小節表明，投影到由 ${\vec {s}}$ 張成的直線上將向量 ${\vec {v}}$ 分解成兩個部分

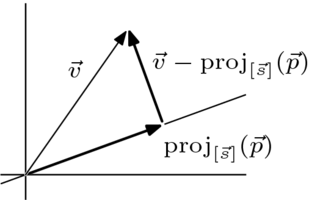
$\displaystyle {\vec {v}}={\mbox{proj}}_{[{\vec {s}}\,]}({\vec {v}})\,+\,\left({\vec {v}}-{\mbox{proj}}_{[{\vec {s}}\,]}({\vec {v}})\right)$

它們是正交的，所以是“不互動的”。我們現在將發展這個建議。

定義 2.1

向量 ${\vec {v}}_{1},\dots ,{\vec {v}}_{k}\in \mathbb {R} ^{n}$ 當任何兩個向量正交時是 **相互正交** 的：如果 $i\neq j$ 那麼點積 ${\vec {v}}_{i}\cdot {\vec {v}}_{j}$ 為零。

定理 2.2

如果集合 $\{{\vec {v}}_{1},\dots ,{\vec {v}}_{k}\}\subset \mathbb {R} ^{n}$ 中的向量是相互正交且非零的，那麼這個集合是線性無關的。

證明

考慮線性關係 $c_{1}{\vec {v}}_{1}+c_{2}{\vec {v}}_{2}+\dots +c_{k}{\vec {v}}_{k}={\vec {0}}$。 如果 $i\in [1..k]$，那麼對等式兩邊與 ${\vec {v}}_{i}$ 進行點積

${\begin{array}{rl}{\vec {v}}_{i}\cdot (c_{1}{\vec {v}}_{1}+c_{2}{\vec {v}}_{2}+\dots +c_{k}{\vec {v}}_{k})&={\vec {v}}_{i}\cdot {\vec {0}}\\c_{i}\cdot ({\vec {v}}_{i}\cdot {\vec {v}}_{i})&=0\end{array}}$

表明，因為 ${\vec {v}}_{i}$ 不為零，則 $c_{i}$ 為零。

推論 2.3

如果一個 $k$ 維空間中的大小為 $k$ 的向量子集是相互正交且非零的，那麼該集合是該空間的基底。

證明

任何線性無關的大小為 $k$ 的 $k$ 維空間的子集是一個基底。

當然，推論 2.3 的逆命題不成立——並非所有 $\mathbb {R} ^{n}$ 的子空間的基底都由相互正交的向量組成。然而，我們可以得到一個部分逆命題，即對於 $\mathbb {R} ^{n}$ 的每一個子空間，至少存在一個由相互正交的向量組成的基底。

示例 2.4

該基底 $\mathbb {R} ^{2}$ 的成員 ${\vec {\beta }}_{1}$ 和 ${\vec {\beta }}_{2}$ 不是正交的。

$\displaystyle B=\left\langle {\begin{pmatrix}4\\2\end{pmatrix}},{\begin{pmatrix}1\\3\end{pmatrix}}\right\rangle$

然而，我們可以從 $B$ 中推匯出同一個空間的新基，該基具有相互正交的成員。對於新基的第一個成員，我們只需使用 ${\vec {\beta }}_{1}$。

${\vec {\kappa }}_{1}={\begin{pmatrix}4\\2\end{pmatrix}}$

對於新基的第二個成員，我們從 ${\vec {\beta }}_{2}$ 中減去其在 ${\vec {\kappa }}_{1}$ 方向上的部分，

$\displaystyle {\vec {\kappa }}_{2}={\begin{pmatrix}1\\3\end{pmatrix}}-{\mbox{proj}}_{\scriptstyle [{\vec {\kappa }}_{1}]}({\begin{pmatrix}1\\3\end{pmatrix}})={\begin{pmatrix}1\\3\end{pmatrix}}-{\begin{pmatrix}2\\1\end{pmatrix}}={\begin{pmatrix}-1\\2\end{pmatrix}}$

這留下了上面圖示的 ${\vec {\kappa }}_{2}$ 部分，它是 ${\vec {\beta }}_{2}$ 的一部分，它與 ${\vec {\kappa }}_{1}$ 正交（根據投影到 ${\vec {\kappa }}_{1}$ 的跨度上的定義，它是正交的）。請注意，根據推論，$\{{\vec {\kappa }}_{1},{\vec {\kappa }}_{2}\}$ 是 $\mathbb {R} ^{2}$ 的基。

定義 2.5

向量空間的正交基是指由相互正交的向量組成的基。

示例 2.6

為了將 $\mathbb {R} ^{3}$ 的

$\left\langle {\begin{pmatrix}1\\1\\1\end{pmatrix}},{\begin{pmatrix}0\\2\\0\end{pmatrix}},{\begin{pmatrix}1\\0\\3\end{pmatrix}}\right\rangle$

轉換成正交基，我們將第一個向量保留原樣。

${\vec {\kappa }}_{1}={\begin{pmatrix}1\\1\\1\end{pmatrix}}$

我們透過從給定的第二個向量 ${\vec {\beta }}_{2}$ 開始，並減去其在 ${\vec {\kappa }}_{1}$ 方向上的部分來獲得 ${\vec {\kappa }}_{2}$。

${\vec {\kappa }}_{2}={\begin{pmatrix}0\\2\\0\end{pmatrix}}-{\mbox{proj}}_{[{\vec {\kappa }}_{1}]}({\begin{pmatrix}0\\2\\0\end{pmatrix}})={\begin{pmatrix}0\\2\\0\end{pmatrix}}-{\begin{pmatrix}2/3\\2/3\\2/3\end{pmatrix}}={\begin{pmatrix}-2/3\\4/3\\-2/3\end{pmatrix}}$

最後，我們得到了 ${\vec {\kappa }}_{3}$，方法是取第三個給定的向量，並減去它在 ${\vec {\kappa }}_{1}$ 方向上的分量，以及它在 ${\vec {\kappa }}_{2}$ 方向上的分量。

${\vec {\kappa }}_{3}={\begin{pmatrix}1\\0\\3\end{pmatrix}}-{\mbox{proj}}_{[{\vec {\kappa }}_{1}]}({\begin{pmatrix}1\\0\\3\end{pmatrix}})-{\mbox{proj}}_{[{\vec {\kappa }}_{2}]}({\begin{pmatrix}1\\0\\3\end{pmatrix}})={\begin{pmatrix}-1\\0\\1\end{pmatrix}}$

再次，推論表明

$\left\langle {\begin{pmatrix}1\\1\\1\end{pmatrix}},{\begin{pmatrix}-2/3\\4/3\\-2/3\end{pmatrix}},{\begin{pmatrix}-1\\0\\1\end{pmatrix}}\right\rangle$

是該空間的一個基。

下一個結果驗證了在這些例子中使用的方法適用於 $\mathbb {R} ^{n}$ 的任何子空間的任何基（我們僅限於 $\mathbb {R} ^{n}$，因為我們還沒有給出其他向量空間的正交性定義）。

定理 2.7（Gram-Schmidt 正交化）

如果 $\left\langle {\vec {\beta }}_{1},\ldots {\vec {\beta }}_{k}\right\rangle$ 是 $\mathbb {R} ^{n}$ 的一個子空間的基，則，其中

${\begin{array}{rl}{\vec {\kappa }}_{1}&={\vec {\beta }}_{1}\\{\vec {\kappa }}_{2}&={\vec {\beta }}_{2}-{\mbox{proj}}_{[{\vec {\kappa }}_{1}]}({{\vec {\beta }}_{2}})\\{\vec {\kappa }}_{3}&={\vec {\beta }}_{3}-{\mbox{proj}}_{[{\vec {\kappa }}_{1}]}({{\vec {\beta }}_{3}})-{\mbox{proj}}_{[{\vec {\kappa }}_{2}]}({{\vec {\beta }}_{3}})\\&\vdots \\{\vec {\kappa }}_{k}&={\vec {\beta }}_{k}-{\mbox{proj}}_{[{\vec {\kappa }}_{1}]}({{\vec {\beta }}_{k}})-\cdots -{\mbox{proj}}_{[{\vec {\kappa }}_{k-1}]}({{\vec {\beta }}_{k}})\end{array}}$

的${\vec {\kappa }}\,$構成同一個子空間的正交基。

證明

我們將使用歸納法來驗證每個 ${\vec {\kappa }}_{i}$ 不為零，且位於 $\left\langle {\vec {\beta }}_{1},\ldots {\vec {\beta }}_{i}\right\rangle$ 的張成空間內，並且與所有前面的向量正交： ${\vec {\kappa }}_{1}\cdot {\vec {\kappa }}_{i}=\cdots ={\vec {\kappa }}_{i-1}\cdot {\vec {\kappa }}_{i}=0$。結合這些，以及 推論 2.3，我們將得到 $\left\langle {\vec {\kappa }}_{1},\ldots {\vec {\kappa }}_{k}\right\rangle$ 是與 $\left\langle {\vec {\beta }}_{1},\ldots {\vec {\beta }}_{k}\right\rangle$ 相同的空間的基。

我們將討論直到 $i=3$ 的情況，這將有助於理解這個論證。完成細節是 問題 15。

當 $i=1$ 時，這個情況是平凡的——設定 ${\vec {\kappa }}_{1}$ 等於 ${\vec {\beta }}_{1}$ 使其成為一個非零向量，因為 ${\vec {\beta }}_{1}$ 是基中的一個成員，它顯然位於所需的張成空間中，並且“與所有前面的向量正交”的條件是空虛成立的。

對於 $i=2$ 的情況，展開 ${\vec {\kappa }}_{2}$ 的定義。

${\vec {\kappa }}_{2}={\vec {\beta }}_{2}-{\mbox{proj}}_{[{\vec {\kappa }}_{1}]}({{\vec {\beta }}_{2}})={\vec {\beta }}_{2}-{\frac {{\vec {\beta }}_{2}\cdot {\vec {\kappa }}_{1}}{{\vec {\kappa }}_{1}\cdot {\vec {\kappa }}_{1}}}\cdot {\vec {\kappa }}_{1}={\vec {\beta }}_{2}-{\frac {{\vec {\beta }}_{2}\cdot {\vec {\kappa }}_{1}}{{\vec {\kappa }}_{1}\cdot {\vec {\kappa }}_{1}}}\cdot {\vec {\beta }}_{1}$

這個展開式表明 ${\vec {\kappa }}_{2}$ 不為零，否則這將是在 ${\vec {\beta }}$ 之間的非平凡線性依賴關係（因為 ${\vec {\beta }}_{2}$ 的係數為 $1$）。它也表明 ${\vec {\kappa }}_{2}$ 在我們期望的生成空間中。最後， ${\vec {\kappa }}_{2}$ 與它前面唯一的向量正交

${\vec {\kappa }}_{1}\cdot {\vec {\kappa }}_{2}={\vec {\kappa }}_{1}\cdot ({\vec {\beta }}_{2}-{\mbox{proj}}_{[{\vec {\kappa }}_{1}]}({{\vec {\beta }}_{2}}))=0$

因為這個投影是正交的。

$i=3$ 的情況與 $i=2$ 的情況相同，除了一個細節。和 $i=2$ 的情況一樣，展開定義

${\begin{array}{rl}{\vec {\kappa }}_{3}&={\vec {\beta }}_{3}-{\frac {{\vec {\beta }}_{3}\cdot {\vec {\kappa }}_{1}}{{\vec {\kappa }}_{1}\cdot {\vec {\kappa }}_{1}}}\cdot {\vec {\kappa }}_{1}-{\frac {{\vec {\beta }}_{3}\cdot {\vec {\kappa }}_{2}}{{\vec {\kappa }}_{2}\cdot {\vec {\kappa }}_{2}}}\cdot {\vec {\kappa }}_{2}\\&={\vec {\beta }}_{3}-{\frac {{\vec {\beta }}_{3}\cdot {\vec {\kappa }}_{1}}{{\vec {\kappa }}_{1}\cdot {\vec {\kappa }}_{1}}}\cdot {\vec {\beta }}_{1}-{\frac {{\vec {\beta }}_{3}\cdot {\vec {\kappa }}_{2}}{{\vec {\kappa }}_{2}\cdot {\vec {\kappa }}_{2}}}\cdot {\bigl (}{\vec {\beta }}_{2}-{\frac {{\vec {\beta }}_{2}\cdot {\vec {\kappa }}_{1}}{{\vec {\kappa }}_{1}\cdot {\vec {\kappa }}_{1}}}\cdot {\vec {\beta }}_{1}{\bigr )}\end{array}}$

表明${\vec {\kappa }}_{3}$ 不為零，並且在該空間內。計算表明${\vec {\kappa }}_{3}$ 與前面的向量${\vec {\kappa }}_{1}$ 正交。

${\begin{array}{rl}{\vec {\kappa }}_{1}\cdot {\vec {\kappa }}_{3}&={\vec {\kappa }}_{1}\cdot {\bigl (}{\vec {\beta }}_{3}-{\mbox{proj}}_{[{\vec {\kappa }}_{1}]}({{\vec {\beta }}_{3}})-{\mbox{proj}}_{[{\vec {\kappa }}_{2}]}({{\vec {\beta }}_{3}}){\bigr )}\\&={\vec {\kappa }}_{1}\cdot {\bigl (}{\vec {\beta }}_{3}-{\mbox{proj}}_{[{\vec {\kappa }}_{1}]}({{\vec {\beta }}_{3}}){\bigr )}-{\vec {\kappa }}_{1}\cdot {\mbox{proj}}_{[{\vec {\kappa }}_{2}]}({{\vec {\beta }}_{3}})\\&=0\end{array}}$

(此處與 $i=2$ 的情況不同—第二行有兩類項。第一項為零，因為此投影是正交的，如同在 $i=2$ 的情況下。第二項為零，因為 ${\vec {\kappa }}_{1}$ 與 ${\vec {\kappa }}_{2}$ 正交，因此也與 ${\vec {\kappa }}_{2}$ 所跨線的任何向量正交。）檢查 ${\vec {\kappa }}_{3}$ 是否也與另一個前一個向量 ${\vec {\kappa }}_{2}$ 正交類似。

除了使基向量正交之外，我們還可以做更多；我們可以透過將每個向量除以其自身的長度來使每個向量長度為一（我們可以對長度進行 **歸一化**）。

示例 2.8

對 示例 2.6 中正交基的每個向量進行長度歸一化，得到此 **標準正交基**。

$\left\langle {\begin{pmatrix}1/{\sqrt {3}}\\1/{\sqrt {3}}\\1/{\sqrt {3}}\end{pmatrix}},{\begin{pmatrix}-1/{\sqrt {6}}\\2/{\sqrt {6}}\\-1/{\sqrt {6}}\end{pmatrix}},{\begin{pmatrix}-1/{\sqrt {2}}\\0\\1/{\sqrt {2}}\end{pmatrix}}\right\rangle$

除了直觀的吸引力和它與標準基${\mathcal {E}}_{n}$ 在 $\mathbb {R} ^{n}$ 中的類比，正交基還簡化了一些計算。例如，參見 練習 9。

練習

問題 1

對 $\mathbb {R} ^{2}$ 的每個基執行 Gram-Schmidt 過程。

1. $\left\langle {\begin{pmatrix}1\\1\end{pmatrix}},{\begin{pmatrix}2\\1\end{pmatrix}}\right\rangle$
2. $\left\langle {\begin{pmatrix}0\\1\end{pmatrix}},{\begin{pmatrix}-1\\3\end{pmatrix}}\right\rangle$
3. $\left\langle {\begin{pmatrix}0\\1\end{pmatrix}},{\begin{pmatrix}-1\\0\end{pmatrix}}\right\rangle$

然後將這些正交基轉換為標準正交基。

建議所有讀者完成此練習。

問題 2

對 $\mathbb {R} ^{3}$ 的每個基執行 Gram-Schmidt 過程。

1. $\left\langle {\begin{pmatrix}2\\2\\2\end{pmatrix}},{\begin{pmatrix}1\\0\\-1\end{pmatrix}},{\begin{pmatrix}0\\3\\1\end{pmatrix}}\right\rangle$
2. $\left\langle {\begin{pmatrix}1\\-1\\0\end{pmatrix}},{\begin{pmatrix}0\\1\\0\end{pmatrix}},{\begin{pmatrix}2\\3\\1\end{pmatrix}}\right\rangle$

然後將這些正交基轉換為標準正交基。

建議所有讀者完成此練習。

問題 3

找到 $\mathbb {R} ^{3}$ 的這個子空間的標準正交基：平面 $x-y+z=0$。

問題 4

找到 $\mathbb {R} ^{4}$ 的這個子空間的標準正交基。

$\{{\begin{pmatrix}x\\y\\z\\w\end{pmatrix}}\,{\big |}\,x-y-z+w=0{\text{ and }}x+z=0\}$

問題 5

證明 $\mathbb {R} ^{n}$ 中的任何線性無關子集都可以正交化，而不會改變其跨度。

建議所有讀者完成此練習。

問題 6

如果我們將 Gram-Schmidt 正交化過程應用於一個已經正交的基，會發生什麼？

問題 7

令 $\left\langle {\vec {\kappa }}_{1},\dots ,{\vec {\kappa }}_{k}\right\rangle$ 是 $\mathbb {R} ^{n}$ 中的一組互相正交的向量。

1. 證明對於空間中的任何 ${\vec {v}}$，向量 ${\vec {v}}-({\mbox{proj}}_{[{\vec {\kappa }}_{1}]}({{\vec {v}}\,})+\dots +{\mbox{proj}}_{[{\vec {v}}_{k}]}({{\vec {v}}\,}))$ 與 ${\vec {\kappa }}_{1}$，…，${\vec {\kappa }}_{k}$ 中的每一個正交。
2. 用 ${\vec {e}}_{1}$ 作為 ${\vec {\kappa }}_{1}$，用 ${\vec {e}}_{2}$ 作為 ${\vec {\kappa }}_{2}$，並將 ${\vec {v}}$ 的分量設定為 $1$，$2$ 和 $3$ 在 $\mathbb {R} ^{3}$ 中說明前一個專案。
3. 證明 ${\mbox{proj}}_{[{\vec {\kappa }}_{1}]}({{\vec {v}}\,})+\dots +{\mbox{proj}}_{[{\vec {v}}_{k}]}({{\vec {v}}\,})$ 是 ${\vec {\kappa }}$ 集合的跨度中最接近 ${\vec {v}}$ 的向量。提示：在前一部分的圖示中，新增向量 $d_{1}{\vec {\kappa }}_{1}+d_{2}{\vec {\kappa }}_{2}$ 並將畢達哥拉斯定理應用於所得三角形。

問題 8

在 $\mathbb {R} ^{3}$ 中找到一個與這兩個向量都正交的向量。

${\begin{pmatrix}1\\5\\-1\end{pmatrix}}\qquad {\begin{pmatrix}2\\2\\0\end{pmatrix}}$

建議所有讀者完成此練習。

問題 9

正交基的一個優點是它們簡化了尋找向量相對於該基的表示。

1. 對於此向量和此非正交基，用於 $\mathbb {R} ^{2}$

   ${\vec {v}}={\begin{pmatrix}2\\3\end{pmatrix}}\qquad B=\left\langle {\begin{pmatrix}1\\1\end{pmatrix}},{\begin{pmatrix}1\\0\end{pmatrix}}\right\rangle$

   首先，將向量相對於基表示出來。然後將向量投影到每個基向量 $[{{\vec {\beta }}_{1}}]$ 和 $[{{\vec {\beta }}_{2}}]$ 的跨度上。
2. 對於 $\mathbb {R} ^{2}$ 的這個正交基

   $K=\left\langle {\begin{pmatrix}1\\1\end{pmatrix}},{\begin{pmatrix}1\\-1\end{pmatrix}}\right\rangle$

   用相同的向量 ${\vec {v}}$ 相對於基表示出來。然後將向量投影到每個基向量的跨度上。請注意，表示和投影中的係數是相同的。
3. 令 $K=\left\langle {\vec {\kappa }}_{1},\ldots ,{\vec {\kappa }}_{k}\right\rangle$ 為 $\mathbb {R} ^{n}$ 的某個子空間的正交基。證明對於子空間中的任何 ${\vec {v}}$，表示 ${\rm {Rep}}_{K}({\vec {v}}\,)$ 的第 $i$ 個分量是來自 ${\mbox{proj}}_{[{\vec {\kappa }}_{i}]}({{\vec {v}}\,})$ 的標量係數 $({\vec {v}}\cdot {\vec {\kappa }}_{i})/({\vec {\kappa }}_{i}\cdot {\vec {\kappa }}_{i})$。
4. 證明 ${\vec {v}}={\mbox{proj}}_{[{\vec {\kappa }}_{1}]}({{\vec {v}}\,})+\dots +{\mbox{proj}}_{[{\vec {\kappa }}_{k}]}({{\vec {v}}\,})$。

問題 10

貝塞爾不等式。考慮以下正交集

$B_{1}=\{{\vec {e}}_{1}\}\quad B_{2}=\{{\vec {e}}_{1},{\vec {e}}_{2}\}\quad B_{3}=\{{\vec {e}}_{1},{\vec {e}}_{2},{\vec {e}}_{3}\}\quad B_{4}=\{{\vec {e}}_{1},{\vec {e}}_{2},{\vec {e}}_{3},{\vec {e}}_{4}\}$

以及向量 ${\vec {v}}\in \mathbb {R} ^{4}$，其分量為 $4$，$3$，$2$ 和 $1$。

1. 找到 ${\vec {v}}$ 向 $B_{1}$ 中向量所張成的空間的投影的係數 $c_{1}$。驗證 $|{\vec {v}}\,|^{2}\geq |c_{1}|^{2}$。
2. 找到 ${\vec {v}}$ 向 $B_{2}$ 中兩個向量所張成的空間的投影的係數 $c_{1}$ 和 $c_{2}$。驗證 $|{\vec {v}}\,|^{2}\geq |c_{1}|^{2}+|c_{2}|^{2}$。
3. 找到與向量 $B_{3}$ 中相關的 $c_{1}$、$c_{2}$ 和 $c_{3}$，以及與向量 $B_{4}$ 中相關的 $c_{1}$、$c_{2}$、$c_{3}$ 和 $c_{4}$。檢查 $|{\vec {v}}\,|^{2}\geq |c_{1}|^{2}+\dots +|c_{3}|^{2}$ 和 $|{\vec {v}}\,|^{2}\geq |c_{1}|^{2}+\dots +|c_{4}|^{2}$。

證明一般情況下成立：其中 $\{{\vec {\kappa }}_{1},\ldots ,{\vec {\kappa }}_{k}\}$ 是一個標準正交集，而 $c_{i}$ 是向量 ${\vec {v}}$ 在該空間上的投影的係數，則 $|{\vec {v}}\,|^{2}\geq |c_{1}|^{2}+\dots +|c_{k}|^{2}$。提示。一種方法是觀察不等式 $0\leq |{\vec {v}}-(c_{1}{\vec {\kappa }}_{1}+\dots +c_{k}{\vec {\kappa }}_{k})|^{2}$ 並展開 $c$。

問題 11

證明或反駁：$\mathbb {R} ^{n}$ 中的每個向量都屬於某個正交基。

問題 12

證明一個 $n\!\times \!n$ 矩陣的列向量構成一個正交集當且僅當該矩陣的逆矩陣等於其轉置。並給出這樣一個矩陣。

問題 13

在 定理 2.2 的證明中，是否忽略了向量集為空的可能性（即 $k=0$）？

問題 14

定理 2.7 描述了從任何基 $B=\left\langle {\vec {\beta }}_{1},\ldots ,{\vec {\beta }}_{k}\right\rangle$ 到正交基 $K=\left\langle {\vec {\kappa }}_{1},\ldots ,{\vec {\kappa }}_{k}\right\rangle$ 的變換。考慮變換矩陣 ${\rm {Rep}}_{B,K}({\mbox{id}})$。

1. 證明矩陣 ${\rm {Rep}}_{K,B}({\mbox{id}})$ （與定理中變換方向相反的基變換）是上三角矩陣，即主對角線以下的所有元素都為零。
2. 證明上三角矩陣的逆矩陣也是上三角矩陣（如果該矩陣可逆）。這表明矩陣 ${\rm {Rep}}_{B,K}({\mbox{id}})$ （按定理中描述的變換方向的基變換）是上三角矩陣。

問題 15

完成 定理 2.7 證明中的歸納論證。

解答