除了我們熟悉的歐幾里得幾何之外,還有其他幾何。 這種幾何出現在藝術中,人們觀察到,觀察者所看到的不一定是存在的。 這是列奧納多·達·芬奇的《最後的晚餐》。
例如,房間裡天花板與左右牆壁交匯的地方實際上是平行線。 然而,觀察者所看到的是幾條線,如果延長,它們將會相交。 交點被稱為*消失點*。 透視的這種方面也很熟悉,比如長長的鐵軌看起來匯聚在遠處的影像。
為了描繪房間,達·芬奇採用了我們如何觀察、如何將三維場景投射到二維影像的模型。 這個模型只是一個第一近似——它沒有考慮我們的視網膜是彎曲的,我們的晶狀體彎曲了光線,我們具有雙眼視覺,以及我們的大腦處理過程極大地影響了我們所看到的東西——但儘管如此,它仍然很有趣,既有藝術意義,也有數學意義。
投影不是正交的,它是一個從單個點到畫布平面的*中心投影*。

(它不是正交投影,因為從觀察者到 的直線不正交於影像平面。) 正如影像所示,中心投影操作保留了一些幾何屬性——直線投射到直線。 然而,它沒有保留其他一些屬性——等長的線段可以投射到不等長的線段;
的直線不正交於影像平面。) 正如影像所示,中心投影操作保留了一些幾何屬性——直線投射到直線。 然而,它沒有保留其他一些屬性——等長的線段可以投射到不等長的線段; 的長度大於
的長度大於 的長度,因為投影到
的長度,因為投影到 的線段更靠近觀察者,更靠近的東西看起來更大。 研究中心投影的影響就是射影幾何。 我們將看到線性代數如何在這項研究中使用。
的線段更靠近觀察者,更靠近的東西看起來更大。 研究中心投影的影響就是射影幾何。 我們將看到線性代數如何在這項研究中使用。
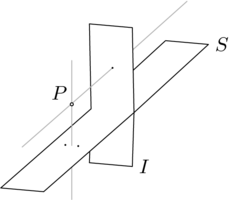
中心投影有三種情況。 第一種是由電影放映機完成的投影。

我們可以認為每個源點都從定義域平面向外“推動”到共域平面中的像點。 這種投影方式與第二種情況有所不同,第二種情況是藝術家將源點“拉回”到畫布上。

在第一種情況下, 在中間,而在第二種情況下,
在中間,而在第二種情況下, 在中間。 還可以使用另一種配置,
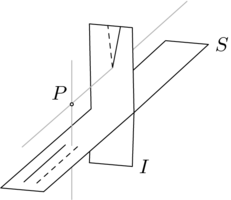
在中間。 還可以使用另一種配置, 在中間。 一個例子就是我們使用針孔將日食的影像照射到一張紙上。
在中間。 一個例子就是我們使用針孔將日食的影像照射到一張紙上。

我們將把這三種情況都視為 對
對 到
到 的中心投影。
的中心投影。
再次考慮鐵軌看起來匯聚到一點的影響。 我們用定義域平面 中的平行線和透過
中的平行線和透過 到共域平面
到共域平面 的投影來模擬這種現象(灰色線平行於
的投影來模擬這種現象(灰色線平行於 ).
).

這裡展示了所有三種投影情況。下面的第一張圖片展示了  像電影放映機一樣,將
像電影放映機一樣,將  的一部分的點投影到
的一部分的點投影到  的下半部分的像點。中間的圖片展示了
的下半部分的像點。中間的圖片展示了  像藝術家一樣,將
像藝術家一樣,將  的另一部分的點拉回到
的另一部分的點拉回到  的中間的像點。在第三張圖片中,
的中間的像點。在第三張圖片中, 像針孔一樣,將
像針孔一樣,將  的點投影到
的點投影到  的上半部分。這幅圖是最難理解的 - 投影到消失點附近的點是那些在
的上半部分。這幅圖是最難理解的 - 投影到消失點附近的點是那些在  的左下角最遠處的點。在
的左下角最遠處的點。在  中靠近垂直灰色線的點被投影到
中靠近垂直灰色線的點被投影到  的高處。
的高處。
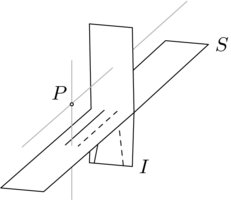

這種情況有兩個尷尬的地方。第一個是,域中兩個最靠近垂直灰色線的點都沒有像,因為從這兩個點進行的投影是沿著與陪域平面平行的灰色線進行的(我們有時說這兩個點被投影“到無窮遠”)。第二個尷尬的地方是,  中的消失點不是來自
中的消失點不是來自  的任何點的像,因為對該點的投影將沿著與域平面平行的灰色線進行(我們有時說消失點是“來自無窮遠”的投影的像)。
的任何點的像,因為對該點的投影將沿著與域平面平行的灰色線進行(我們有時說消失點是“來自無窮遠”的投影的像)。
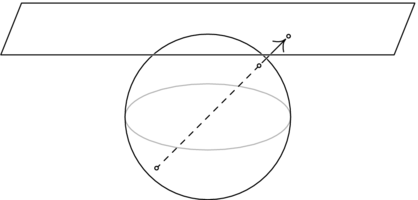
為了獲得更好的模型,將投影儀  放在原點。想象一下
放在原點。想象一下  被一個玻璃半球形圓頂覆蓋。當
被一個玻璃半球形圓頂覆蓋。當  向外看時,視線中的任何物體都會投射到圓頂上的同一個點。這包括
向外看時,視線中的任何物體都會投射到圓頂上的同一個點。這包括  和圓頂之間的線上的物體,例如電影投影儀的投影。它還包括距離
和圓頂之間的線上的物體,例如電影投影儀的投影。它還包括距離  比圓頂更遠的線上的物體,例如畫家進行投影的情況。它還包括位於
比圓頂更遠的線上的物體,例如畫家進行投影的情況。它還包括位於  後面的線上的物體,例如針孔投影的情況。
後面的線上的物體,例如針孔投影的情況。

從這個角度看  ,線上的所有點都被視為同一個點。 因此,對於任何非零向量
,線上的所有點都被視為同一個點。 因此,對於任何非零向量  ,我們定義相關的 投影平面上的點
,我們定義相關的 投影平面上的點  為集合
為集合  ,該集合包含所有非零向量,這些向量與
,該集合包含所有非零向量,這些向量與  在透過原點的同一條直線上。為了描述一個投影點,我們可以給出這條直線的任何代表成員,因此上面顯示的投影點可以用以下三種方式中的任何一種表示。
在透過原點的同一條直線上。為了描述一個投影點,我們可以給出這條直線的任何代表成員,因此上面顯示的投影點可以用以下三種方式中的任何一種表示。

這些都是  的 齊次座標向量。
的 齊次座標向量。
這幅圖以及它所產生的上述定義澄清了中心投影的描述,但圓頂模型中存在一些令人困惑的地方:如果觀察者向下看會怎樣?如果我們畫出 的視線,使得視線朝著我們,即離開頁面的一端,向下延伸到圓頂下方,然後我們可以沿視線方向向後追蹤,向上越過
的視線,使得視線朝著我們,即離開頁面的一端,向下延伸到圓頂下方,然後我們可以沿視線方向向後追蹤,向上越過 ,朝向半球背面,即頁面後面的部分。因此,在圓頂模型中,向下看會得到一個位於觀察者身後的投影點。因此,如果上圖中的觀察者將視線降至圓頂底部,那麼投影點也會下降,並且隨著視線繼續向下延伸穿過赤道,投影點會突然從圓頂正面轉移到圓頂背面。這種圖紙上的不連續性意味著我們通常需要將赤道點視為一個單獨的案例。也就是說,雖然中心投影的鐵路軌道討論有三種情況,但圓頂模型只有兩種。
,朝向半球背面,即頁面後面的部分。因此,在圓頂模型中,向下看會得到一個位於觀察者身後的投影點。因此,如果上圖中的觀察者將視線降至圓頂底部,那麼投影點也會下降,並且隨著視線繼續向下延伸穿過赤道,投影點會突然從圓頂正面轉移到圓頂背面。這種圖紙上的不連續性意味著我們通常需要將赤道點視為一個單獨的案例。也就是說,雖然中心投影的鐵路軌道討論有三種情況,但圓頂模型只有兩種。
我們可以做得更好。考慮一個以原點為中心的球體。透過原點的任何直線都與球體相交於兩點,這兩點被稱為對映點。因為我們將透過原點的每條直線與投影平面上的一個點相關聯,所以我們可以將這樣的點繪製為球體上的兩個對映點。在下圖中,這兩個對映點用虛線連線,以強調它們不是兩個不同的點,這兩個點的組合構成一個投影點。

雖然將點繪製為一對對映點不如每點一個點的圓頂模型自然,但另一方面,圓頂模型的尷尬之處消失了,因為當視線從北向南滑動時,影像上不會出現突然的變化。這種中心投影模型是均勻的——三種情況簡化為一種。
到目前為止,我們已經描述了投影幾何中的點。那麼線呢?觀察者在原點看到的直線在下圖中顯示為一個大圓,即模型球體與透過原點的平面相交的部分。

(這條直線上的一個投影點顯示出一種微妙之處。因為兩個對映點組合構成一個投影點,所以大圓的頁面背面部分與頁面正面部分是同一組投影點。) 正如我們對每個投影點所做的那樣,我們也將用三個實數來描述投影直線。例如,透過 中的原點的這個平面中的成員
中的原點的這個平面中的成員

投影到一條可以用三重數 描述的直線上(我們使用行向量在排版上區分直線和點)。一般來說,對於任何非零的三維行向量
描述的直線上(我們使用行向量在排版上區分直線和點)。一般來說,對於任何非零的三維行向量 ,我們將與之關聯的投影平面上的直線定義為集合
,我們將與之關聯的投影平面上的直線定義為集合 ,它是由
,它是由 的非零倍陣列成的。
的非零倍陣列成的。
將直線描述為三元組的原因在於,在射影平面中,點  和直線
和直線  是 **關聯** 的——點在直線上,直線經過點——當且僅當它們的代表向量
是 **關聯** 的——點在直線上,直線經過點——當且僅當它們的代表向量  的點積為零(問題 4 表明這與代表向量
的點積為零(問題 4 表明這與代表向量  和
和  的選擇無關)。例如,上面由分量為
的選擇無關)。例如,上面由分量為  的列向量描述的射影點位於由
的列向量描述的射影點位於由  描述的射影直線上,僅僅是因為
描述的射影直線上,僅僅是因為  中任何分量比例為
中任何分量比例為  的向量都位於透過原點的平面上,其方程形式為
的向量都位於透過原點的平面上,其方程形式為  ,其中
,其中  為非零值。也就是說,關聯公式是
為非零值。也就是說,關聯公式是  和
和  是三維空間中的直線和平面投影的結果。
是三維空間中的直線和平面投影的結果。
因此,我們可以進行解析射影幾何。例如,射影直線  的方程為
的方程為  ,因為位於直線上的點都具有其代表向量滿足此方程的性質。與熟悉的歐幾里德解析幾何不同的是,在射影幾何中我們討論的是點的方程。對於一個固定的點,例如
,因為位於直線上的點都具有其代表向量滿足此方程的性質。與熟悉的歐幾里德解析幾何不同的是,在射影幾何中我們討論的是點的方程。對於一個固定的點,例如

透過該點的直線(即與該點相交的直線)的特徵是,任何代表直線的向量的分量都滿足  ,因此,這就是
,因此,這就是  的方程。
的方程。
關於直線和點的陳述的對稱性揭示了射影幾何的對偶原理:在任何真命題中,將“點”與“直線”互換,得到的仍然是一個真命題。例如,正如兩點確定一條直線,在射影平面上,兩條直線確定一個點。下圖顯示了兩條直線在對蹠點相交,因此在射影平面上相交於一個點。


將此與歐幾里得幾何進行對比,在歐幾里得幾何中,兩條不同的直線可能有一個唯一的交點,也可能平行。這樣,射影幾何比歐幾里得幾何更簡單、更統一。
這種簡單性很重要,因為歐幾里得幾何和射影幾何之間存在聯絡:射影平面可以看作是歐幾里得平面的擴充套件。以球面模型表示射影平面,即  中的單位球,並將歐幾里得空間視為平面
中的單位球,並將歐幾里得空間視為平面  。這使我們能夠將射影空間中的某些點視為對應於歐幾里得空間中的點,因為平面上所有點都是球面上對蹠點的投影。
。這使我們能夠將射影空間中的某些點視為對應於歐幾里得空間中的點,因為平面上所有點都是球面上對蹠點的投影。

注意,赤道上的射影點不會投影到平面上。相反,它們投影到“無窮遠”。因此,我們可以認為射影空間由歐幾里得平面加上一些附加點組成——歐幾里得平面嵌入在射影平面上。 這些附加點,即赤道上的點,被稱為理想點或無窮遠點,而赤道被稱為理想線或無窮遠線(注意,它不是歐幾里得直線,而是一條射影直線)。
擴充套件到射影平面的優勢在於,歐幾里得幾何中的一些尷尬之處消失了。例如,上面在  中所示的射影直線在球面赤道上,即對蹠點處,相交於一個射影點。如果我們將這些直線放入
中所示的射影直線在球面赤道上,即對蹠點處,相交於一個射影點。如果我們將這些直線放入  中,它們對應於歐幾里得幾何中的平行直線。也就是說,從歐幾里得平面到射影平面的變換,將直線相交或平行兩種情況,統一成了直線相交(可能在無窮遠點相交)一種情況。
中,它們對應於歐幾里得幾何中的平行直線。也就是說,從歐幾里得平面到射影平面的變換,將直線相交或平行兩種情況,統一成了直線相交(可能在無窮遠點相交)一種情況。
在許多方面,射影幾何比歐幾里得幾何更“優雅”,但問題在於我們對它沒有相同的經驗或直覺。這是做解析幾何的一個優勢,解析幾何中方程可以引導我們得出正確的結論。解析射影幾何使用線性代數。例如,對於射影平面上的三個點  ,透過固定表示每個點的向量,建立這些點的方程,可以看出,當且僅當由此得到的三個方程組有無窮多個表示該直線的行向量解時,這三個點是共線的——位於一條直線上。而這又等價於以下行列式為零。
,透過固定表示每個點的向量,建立這些點的方程,可以看出,當且僅當由此得到的三個方程組有無窮多個表示該直線的行向量解時,這三個點是共線的——位於一條直線上。而這又等價於以下行列式為零。

因此,射影平面上的三個點是共線的,當且僅當任何三個代表它們的列向量線性相關。類似地(這也說明了對偶原理),射影平面上的三條直線交於一點,當且僅當任何三個表示它們的列向量線性相關。
以下結果進一步證明了射影平面幾何的“優雅”,與歐幾里得幾何相比。 這兩個三角形被稱為從  透視,因為它們的對應頂點是共線的。
透視,因為它們的對應頂點是共線的。

考慮對應邊的配對:邊  ,邊
,邊  ,以及邊
,以及邊  。德薩格定理指出,當三對對應邊延伸成直線時,它們會相交(這裡顯示為點
。德薩格定理指出,當三對對應邊延伸成直線時,它們會相交(這裡顯示為點  ,點
,點  ,以及點
,以及點  ), 而且,這三個交點是共線的。
), 而且,這三個交點是共線的。
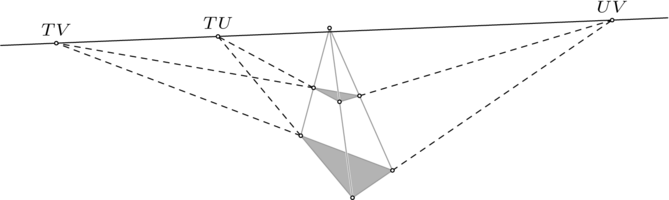
我們將使用射影幾何來證明這個定理。(這些被畫成了歐幾里得圖形,因為這是更熟悉的影像。為了將它們視為射影圖形,我們可以想象,儘管所示的線段是圓弧的一部分,並且是彎曲的,但模型的半徑與圖形大小相比非常大,因此,在這個草圖中,邊看起來是直的。)
對於這個證明,我們需要一個初步的引理 (Coxeter 1974):如果  是射影平面上的四個點(其中沒有三個點是共線的),那麼存在射影點的齊次座標向量
是射影平面上的四個點(其中沒有三個點是共線的),那麼存在射影點的齊次座標向量  ,以及
,以及  的基
的基  ,滿足以下條件。
,滿足以下條件。

證明很簡單。因為 不在同一條射影線上,任何齊次座標向量
不在同一條射影線上,任何齊次座標向量 不在
不在 中透過原點的同一平面上,因此構成
中透過原點的同一平面上,因此構成 的一個生成集。因此,
的一個生成集。因此, 的任何齊次座標向量都可以寫成組合
的任何齊次座標向量都可以寫成組合 。然後,我們可以取
。然後,我們可以取

其中基為 。
。
現在,為了證明德薩格定理,使用引理來固定齊次座標向量和基。

因為投影點  與投影線
與投影線  相交,則
相交,則  的任何齊次座標向量都位於
的任何齊次座標向量都位於  中以原點為起點,由
中以原點為起點,由  和
和  的齊次座標向量所跨越的平面上。
的齊次座標向量所跨越的平面上。

對於一些標量  和
和  。也就是說,線
。也就是說,線  上的成員
上的成員  的齊次座標向量形式如左下方所示,而
的齊次座標向量形式如左下方所示,而  的形式類似。
的形式類似。

投影線  是
是  中過原點的平面的像。一個快速獲得其方程的方法是注意到其中的任何向量都線性依賴於
中過原點的平面的像。一個快速獲得其方程的方法是注意到其中的任何向量都線性依賴於  和
和  的向量,因此該行列式為零。
的向量,因此該行列式為零。

在  中,其像為投影線
中,其像為投影線  的平面的方程如下。
的平面的方程如下。

找到這兩個的交點是例行的。

(當然,這是投影點的齊次座標向量。)另外兩個交點類似。

證明透過注意到這些投影點位於同一條投影線上而完成,因為三個齊次座標向量的和為零。
每個射影定理都可以轉化為歐幾里得版本,雖然歐幾里得結果在陳述和證明上通常更復雜。德扎格定理就很好地說明了這一點。在轉化為歐幾里得空間時,當  位於理想線上時,必須單獨處理,因為此時直線
位於理想線上時,必須單獨處理,因為此時直線  平行。
平行。
德扎格定理陳述後面的括號備註建議將歐幾里得影像視為射影幾何中的圖形,以作為半徑非常大的模型。也就是說,正如地球上的一個小區域對居住在那裡的人來說看起來是平坦的,射影平面也是“區域性歐幾里得”的。
雖然射影平面的區域性性質是熟悉的歐幾里得性質,但它有一個全域性性質與歐幾里得性質完全不同。下面的圖片顯示了一個射影點。在這個點上畫了一個  -軸。這個軸在球體的對極端點處出現的形式非常有趣。在北半球,軸以黑色繪製,右手將手指放在
-軸。這個軸在球體的對極端點處出現的形式非常有趣。在北半球,軸以黑色繪製,右手將手指放在  -軸上,拇指將指向
-軸上,拇指將指向  -軸。但對極軸正好相反:將右手放在
-軸。但對極軸正好相反:將右手放在  -軸上,拇指將指向錯誤的方向,相反,是左手才能正常運作。簡而言之,射影平面不可定向:在這種幾何中,左右手性不是圖形的固定屬性。
-軸上,拇指將指向錯誤的方向,相反,是左手才能正常運作。簡而言之,射影平面不可定向:在這種幾何中,左右手性不是圖形的固定屬性。

下面的一系列圖片戲劇性地展現了這種不可定向性。它們描繪了沿  部分的
部分的  -軸在這個空間中旅行。(警告:顯示的旅行不是半圈,而是全圈。誠然,如果我們把這個變成電影,那麼我們可以看到上面圖畫中北半球的點逐漸繞球體旋轉大約半圈,到達下面最後一張圖片。而且我們可以看到上面圖片中南半球的點滑過南極,向上穿過赤道,到達最後一張圖片。但是:虛線兩端點的點是同一個射影點。我們不需要繼續走很遠;到最後一張圖片時,我們幾乎回到了開始的射影點。)
-軸在這個空間中旅行。(警告:顯示的旅行不是半圈,而是全圈。誠然,如果我們把這個變成電影,那麼我們可以看到上面圖畫中北半球的點逐漸繞球體旋轉大約半圈,到達下面最後一張圖片。而且我們可以看到上面圖片中南半球的點滑過南極,向上穿過赤道,到達最後一張圖片。但是:虛線兩端點的點是同一個射影點。我們不需要繼續走很遠;到最後一張圖片時,我們幾乎回到了開始的射影點。)





在迴路結束時, 部分的
部分的  -軸以相反的方向伸出。因此,在射影平面中,我們無法將圖形描述為右手或左手(另一種表達方式是我們無法將螺旋線描述為順時針或逆時針)。
-軸以相反的方向伸出。因此,在射影平面中,我們無法將圖形描述為右手或左手(另一種表達方式是我們無法將螺旋線描述為順時針或逆時針)。
這種非定向空間存在的展示提出了一個問題,即我們的宇宙是否可定向:宇航員是否有可能以右手狀態離開,以左手狀態返回?一個很好的非技術參考是 (Gardner 1990)。關於方向反轉的經典科幻故事是 (Clarke 1982)。
所以射影幾何在數學上很有趣,除了它在藝術中自然出現的形式之外。它不僅僅是縮短某些證明的技術手段。有關概述,請參見 (Courant & Robbins 1978)。我們在這裡採用的方法,即分析方法,可以得出快速定理,而且——對我們來說最重要的是——它說明了線性代數的力量(參見 Hanes (1990), Ryan (1986), 和 Eggar (1998))。但是,另一種方法,即從公理系統推匯出結果的合成方法,既極其美妙,也是發展的歷史路線。兩種關於這種方法的優秀來源是 (Coxeter 1974) 或 (Seidenberg 1962)。一個有趣且容易的應用是 (Davies 1990)。
- 問題 1
這個點的方程是什麼?

- 問題 2
- 在射影平面上找到經過這兩個點的直線。

- 找到同時經過這兩條射影直線的點。

- 問題 3
找出經過兩個射影點的直線的公式。找出經過兩個射影直線的點的公式。
- 問題 4
證明入射定義與 和
和  代表的選擇無關。也就是說,如果
代表的選擇無關。也就是說,如果  和
和  是
是  的兩個齊次座標三元組,而
的兩個齊次座標三元組,而  和
和  是
是  的兩個齊次座標三元組,證明
的兩個齊次座標三元組,證明  當且僅當
當且僅當  。
。
- 問題 5
畫圖說明中心投影不保持圓形,圓形可能投影成橢圓形。一個(非圓形)橢圓形可以投影成圓形嗎?
- 問題 6
給出射影平面反極點模型的非赤道部分與平面  之間的對應公式。
之間的對應公式。
- 問題 7
(帕普斯定理) 假設  是共線的,並且
是共線的,並且  也是共線的。考慮以下三個點
也是共線的。考慮以下三個點
- 直線
 的交點
的交點 
- 直線
 的交點
的交點 
- 直線
 和
和  的交點
的交點 
- 畫一個(歐幾里得)圖形。
- 應用德薩格定理中使用的引理,為
 和
和  獲取簡單的齊次座標向量。
獲取簡單的齊次座標向量。
- 找到
 的結果齊次座標向量(這些向量必須包含一個引數,例如,
的結果齊次座標向量(這些向量必須包含一個引數,例如, 可以位於
可以位於  線上的任何位置)。
線上的任何位置)。
- 找到
 的結果齊次座標向量。(提示:它包含兩個引數。)
的結果齊次座標向量。(提示:它包含兩個引數。)
- 找到
 的結果齊次座標向量。(它也包含兩個引數。)
的結果齊次座標向量。(它也包含兩個引數。)
- 證明三個引數的乘積為 1。
- 驗證
 是否在
是否在  直線上。
直線上。
解決方案
- 克拉克,亞瑟·C. (1982), 偉大的科幻故事 8:技術錯誤, DAW Books.
- 庫朗,理查德;羅賓斯,赫伯特 (1978), 什麼是數學?, 牛津大學出版社.
- 考克斯特,H.S.M. (1974), 射影幾何 (第二版), 施普林格出版社.
- 戴維斯,托馬斯·D. (1990), “新的證據表明皮爾裡到達了北極”,國家地理雜誌, 177 (1): 44 .
- 埃加,M.H. (1998), “針孔相機、透視和射影幾何”,美國數學月刊, 美國數學學會: 618–630 .
- 加德納,馬丁 (1990), 新左右對稱宇宙 (第三修訂版), W. H. Freeman and Company.
- 漢斯,基特 (1990), “解析射影幾何及其應用”,UMAP 模組 (UMAP UNIT 710): 111.
- 瑞安,帕特里克·J. (1986), 歐幾里得和非歐幾里得幾何:解析方法, 劍橋大學出版社.
- 塞登伯格,A. (1962), 射影幾何講義, 範·諾斯特蘭德.


















































































































