在我們以最廣泛的意義討論拓撲空間之前,我們將首先關注一種特殊的拓撲空間,即度量空間。這個抽象有大量的有用特例,因此值得我們特別關注。此外,這個抽象生動形象且易於理解;它將最終引導我們進入拓撲空間的完整抽象。
一個 度量空間 是一個 笛卡爾對  其中
其中  是一個非空的 集合 並且
是一個非空的 集合 並且  ,是一個被稱為度量的函式,它滿足以下要求:對於所有
,是一個被稱為度量的函式,它滿足以下要求:對於所有 
 當且僅當
當且僅當 
 (對稱性)
(對稱性) (三角不等式)
(三角不等式)
請注意,有些作者不要求度量空間非空。當我們談論具有度量  的度量空間
的度量空間  時,我們將用
時,我們將用  來表示。
來表示。
- 一個重要的例子是離散度量。它可以定義在任何非空集合 X 上,如下所示

- 在實數集
 上,定義
上,定義  (
( 和
和  之間的絕對距離)。
之間的絕對距離)。
為了證明這確實是一個度量空間,我們必須證明  確實是度量。首先,對於任何實數
確實是度量。首先,對於任何實數  和
和  ,
, 。
。


- 將平面
 作為空間,並設
作為空間,並設  .
.
- 這是
 和
和  之間的歐幾里得距離。
之間的歐幾里得距離。
- 我們可以將前面兩個例子進行推廣。設
 為一個 賦範向量空間(在
為一個 賦範向量空間(在  或
或  上)。我們可以定義度量為:
上)。我們可以定義度量為: 。因此每個賦範向量空間都是一個度量空間。
。因此每個賦範向量空間都是一個度量空間。
- 對於向量空間
 ,我們有一個有趣的範數。設
,我們有一個有趣的範數。設  和
和  是
是  的兩個向量。我們定義 p-範數:
的兩個向量。我們定義 p-範數: 。對於每個
。對於每個  -範數,都存在一個基於它的度量。
-範數,都存在一個基於它的度量。 的一些有趣情況是:
的一些有趣情況是:
- 球體上兩點之間的 大圓距離 是一個度量。
- 希爾伯特空間是定義在無限序列空間上的一個度量空間,這個空間包含所有滿足
 收斂的無限序列
收斂的無限序列  。其度量定義為
。其度量定義為  。
。
**埃爾德什數**的概念暗示了在所有數學家集合上定義的度量。假設  是兩位數學家,我們定義
是兩位數學家,我們定義  為:
為:
這個度量很容易推廣到任何自反關係(或無向圖,兩者是一樣的)。
請注意,如果我們改為定義  為
為  的 Erdős 數之和,那麼
的 Erdős 數之和,那麼  將不會是一個度量,因為它將不滿足
將不會是一個度量,因為它將不滿足  。例如,如果
。例如,如果  = Stanisław Ulam,那麼
= Stanisław Ulam,那麼  。
。
在本章中,我們將參考度量空間。每個度量空間都帶有一個度量函式。因此,度量函式可能不會被明確提及。這有幾個原因。
- 我們不想讓文字過於模糊。
- 我們對它沒有特殊之處要說。
- 該空間具有“自然”度量。例如,
 的“自然”度量是歐幾里得度量
的“自然”度量是歐幾里得度量  。
。
由於這是一個維基百科頁面,如果出於某種原因您認為度量值得提及,您可以更改文字(如果您確定自己知道自己在做什麼)或在討論頁面上報告它。
開球是度量空間拓撲的基本要素。我們將透過它來定義直觀的拓撲定義(稍後將轉換為真正的拓撲定義),並將微積分中性質的定義(例如收斂性和連續性)直觀地轉換為拓撲定義。我們將嘗試展示度量空間的許多定義如何也可以用“開球語言”寫出來。然後我們可以立即將定義轉換為拓撲定義。
給定一個度量空間  ,以
,以  為中心、半徑為
為中心、半徑為  的 **開****球** 定義為集合
的 **開****球** 定義為集合

直觀地說,它是空間中所有距離某個點  小於
小於  的所有點。
的所有點。
為什麼這被稱為球?讓我們看看 的情況。
的情況。

因此  正是
正是  – 以
– 以  為中心,半徑為
為中心,半徑為  的球體。在
的球體。在  中,球被稱為 開球,因為它不包含球體 (
中,球被稱為 開球,因為它不包含球體 ( )。
)。
單位球 是半徑為 1 的球。讓我們來看一些
 單位球的例子,它們具有不同的
單位球的例子,它們具有不同的 -範數誘導度量。具有範數
-範數誘導度量。具有範數  的
的  單位球是
單位球是
![{\displaystyle B_{1}{\bigl (}(0,0){\bigr )}={\Big \{}(x,y)\in \mathbb {R} ^{2}:d{\bigl (}(x,y),(0,0){\bigr )}<1{\Big \}}={\Big \{}(x,y):{\bigl \|}(x,y)-(0,0){\bigr \|}_{p}<1{\Big \}}={\Big \{}(x,y):\|(x,y)\|_{p}<1{\Big \}}={\Big \{}(x,y):{\sqrt[{p}]{|x|^{p}+|y|^{p}}}<1{\Big \}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b8ebf9c0bf5f2d66d2fe08844d3548e60e3a9868)
- 由
 誘導的度量,在這種情況下,單位球為:
誘導的度量,在這種情況下,單位球為:
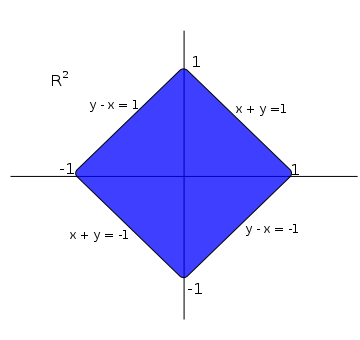
- 由
 誘導的度量,在這種情況下,單位球為:
誘導的度量,在這種情況下,單位球為:

- 由
 誘導的度量,在這種情況下,單位球為:
誘導的度量,在這種情況下,單位球為:

正如我們所見,單位球並不一定像真正的球體。事實上,有時單位球可以是一個點。
- 離散度量,單位球為

定義:我們說 x 是 A 的內部點iff 存在一個 使得:
使得: 。直觀地講,這意味著 x 確實在 A '內部' - 因為它包含在 A 內部的一個球體中 - 它不靠近 A 的邊界。
。直觀地講,這意味著 x 確實在 A '內部' - 因為它包含在 A 內部的一個球體中 - 它不靠近 A 的邊界。
圖示
| 內部點 |
非內部點 |
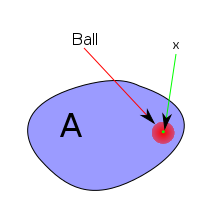
|

|
定義:集合 A 的內部 是 A 中所有內部點的集合。集合 A 的內部用  表示。有用的符號:
表示。有用的符號: 和
和  .
.
int 的一些基本性質(對於任何集合 A,B)




第一個的證明
我們需要證明: 。但這很容易!根據定義,我們有
。但這很容易!根據定義,我們有  ,因此
,因此 
第二個的證明
為了證明  ,我們需要證明
,我們需要證明  和
和  。
。
"  " 方向已經證明:對於任意集合 A,如果
" 方向已經證明:對於任意集合 A,如果  ,那麼把
,那麼把  作為該集合,我們得到
作為該集合,我們得到  。
。
"  " 方向
" 方向
令  。我們需要證明
。我們需要證明  。
。
如果  ,那麼存在一個球
,那麼存在一個球  。現在,球
。現在,球  中的每一個點 y 都是 A 的內部點(在
中的每一個點 y 都是 A 的內部點(在  內部),因為在它周圍存在一個在 A 內部的球:
內部),因為在它周圍存在一個在 A 內部的球: 。
。
我們有 (因為其中的每個點都在
(因為其中的每個點都在 裡面)並且根據定義
裡面)並且根據定義 .
.
提示:為了更好地理解,請自己畫出 .
.
其餘證明留給讀者。
- [a, b] : 所有滿足
 的點 x
的點 x
- (a, b) : 所有滿足
 的點 x
的點 x
對於度量空間 (直線),我們有
(直線),我們有
![{\displaystyle int([a,b])=(a,b)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd3d977333a969ec5d8d06a91b7021d52842188f)
![{\displaystyle int((a,b])=(a,b)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bfed9af226d984832f234c50d6da2f32e3142aed)


讓我們證明第一個例子 (![{\displaystyle int([a,b])=(a,b)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd3d977333a969ec5d8d06a91b7021d52842188f) )。令
)。令  (即:
(即: ),我們將證明
),我們將證明  是一個內點。
是一個內點。
令  。請注意
。請注意  和
和  。因此
。因此  。
。
我們現在已經證明了  中的每個點 x 都是一個內點。現在點
中的每個點 x 都是一個內點。現在點  呢?讓我們證明它們 不是 內點。如果
呢?讓我們證明它們 不是 內點。如果  是
是 ![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) 的一個內點,那麼就存在一個球
的一個內點,那麼就存在一個球 ![{\displaystyle B_{\epsilon }(a)\subset [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b62496930755059267ae3e9c396cba3aca37dd0) 。但這將意味著,點
。但這將意味著,點  位於
位於 ![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) 內部。但由於
內部。但由於  ,這是一個矛盾。我們以類似的方式證明 b 不是內點。
,這是一個矛盾。我們以類似的方式證明 b 不是內點。
總之,集合  包含
包含 ![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) 的 所有 內點。我們可以標記
的 所有 內點。我們可以標記 ![{\displaystyle int([a,b])=(a,b)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd3d977333a969ec5d8d06a91b7021d52842188f)
在度量空間中,如果一個集合等於它的內部 ( ),則稱該集合在度量空間中是開集。當我們遇到拓撲空間時,我們將對開集的定義進行推廣。然而,在度量空間中開集的定義與將我們的度量空間視為拓撲空間時的定義相同。
),則稱該集合在度量空間中是開集。當我們遇到拓撲空間時,我們將對開集的定義進行推廣。然而,在度量空間中開集的定義與將我們的度量空間視為拓撲空間時的定義相同。
性質
- 空集是一個開集(根據定義:
 )。
)。
- 開球是一個開集。
- 對於任何集合 B,int(B) 是一個開集。這很容易看出,因為:int(int(B))=int(B)。
- 如果 A,B 是開集,那麼
 是開集。因此,開集的有限交集是開集。
是開集。因此,開集的有限交集是開集。
- 如果
 (對於任何指標集 I)是開集,那麼它們的並集
(對於任何指標集 I)是開集,那麼它們的並集  是開集。
是開集。
證明 2
令  為一個開球。令
為一個開球。令  。那麼
。那麼  。
。
在下圖中,綠線表示  ,棕色線表示
,棕色線表示  。我們找到了一個包含
。我們找到了一個包含  的球體在
的球體在  內。
內。 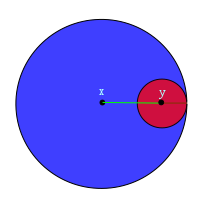
證明 4
假設 A 和 B 是開集,我們需要證明  。根據內部點的第一個性質,我們只需要證明
。根據內部點的第一個性質,我們只需要證明  ,這意味著
,這意味著  。令
。令  。我們知道,根據前提 A 和 B 是開集以及
。我們知道,根據前提 A 和 B 是開集以及  ,存在兩個球:
,存在兩個球:  。令
。令  ,我們有
,我們有  。根據內部點的定義,我們有
。根據內部點的定義,我們有  (
( 是所需的球)。
是所需的球)。
有趣的是,這個性質對於無限個開集的交集並不一定成立。在實數軸上,我們可以看一個例子:令  。然後我們看到
。然後我們看到  ,它是閉集。
,它是閉集。
證明 5
證明開集的並集是開集是相當簡單的:令 (對於任何指標集I)是開集的集合。我們需要證明
(對於任何指標集I)是開集的集合。我們需要證明 :如果
:如果 ,那麼它有一個球
,那麼它有一個球 。使某個點在
。使某個點在 中成為內點的同一個球也會使它在
中成為內點的同一個球也會使它在 中成為內點。
中成為內點。
命題:一個集合是開集,當且僅當它是開球的並集。
證明:令A是一個開集。根據定義,如果 ,則存在一個球
,則存在一個球 。然後我們可以將A寫成:
。然後我們可以將A寫成: 。等式成立是因為:
。等式成立是因為: ,因為
,因為 。
。  ,因為在每個球中我們都有元素
,因為在每個球中我們都有元素 ,我們對A的所有元素的球進行並集。
,我們對A的所有元素的球進行並集。
另一方面,開球的並集是開集,因為任意開集的並集都是開集。
- 正如我們所見,每個開球都是一個開集。
- 對於每個具有離散度量的空間
 ,每個集合都是開集。
,每個集合都是開集。
證明:令  為一個集合。我們需要證明,如果
為一個集合。我們需要證明,如果  ,那麼
,那麼  是一個內點。讓我們使用以
是一個內點。讓我們使用以  為中心,半徑為
為中心,半徑為  的球。我們有
的球。我們有  。因此
。因此  是一個內點。
是一個內點。
- 空間
 具有常規度量。每個開區間
具有常規度量。每個開區間  是一個開集。該證明類似於證明
是一個開集。該證明類似於證明 ![{\displaystyle int([a,b])=(a,b)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd3d977333a969ec5d8d06a91b7021d52842188f) ,我們已經見過。
,我們已經見過。
在任何度量空間 X 中,以下三個陳述成立
- 1) 任意多個開集的並集是開集。
- 證明:令
 為一個開集集合,並令
為一個開集集合,並令 。那麼存在一個
。那麼存在一個  使得
使得  。
。- 所以存在一個
 使得
使得  。因此
。因此
 .
.
- 2) 有限多個開集的交集是開集。
- 證明: 令
 ,其中
,其中  是一個有限的開集集合。
是一個有限的開集集合。- 所以對於每個
 ,有
,有  。令
。令  。對於每個
。對於每個  ,存在一個
,存在一個  ,使得
,使得  。令
。令  {
{ }。因此
}。因此  且
且  。
。
- 3) 空集和 X 都是開集。
在任何度量空間 X 中,以下語句成立
- 1) 任意數量閉集的交集是閉集。
- 2) 有限數量閉集的並集是閉集。
首先,讓我們將微積分中收斂的定義翻譯成“度量空間”的語言:我們說一個序列  收斂於
收斂於  ,如果對於任意
,如果對於任意  ,都存在一個
,都存在一個  ,使得對於任意
,使得對於任意  ,以下條件成立:
,以下條件成立: 。
。
等價地,我們可以使用開球來定義收斂:一個序列  收斂於
收斂於  ,如果對於任意
,如果對於任意  ,都存在一個
,都存在一個  ,使得對於任意
,使得對於任意  ,以下條件成立:
,以下條件成立: 。
。
後一種定義使用“開球”的語言,但我們可以做得更好——我們可以從收斂定義中刪除 ,從而使定義更具拓撲性。讓我們定義
,從而使定義更具拓撲性。讓我們定義 收斂到
收斂到 (並標記
(並標記 ),如果對於每個球
),如果對於每個球 圍繞
圍繞 ,存在
,存在 ,對於每個
,對於每個 ,以下成立:
,以下成立: 。
。 被稱為該序列的極限。
被稱為該序列的極限。
這些定義都是一樣的,但後者使用拓撲術語,可以很容易地轉換為以後的拓撲定義。
- 如果一個序列有極限,那麼它只有一個極限。
證明 設一個序列  有兩個極限,
有兩個極限, 和
和  。如果它們不相同,我們必須有
。如果它們不相同,我們必須有  。設
。設  小於此距離。現在對於某個
小於此距離。現在對於某個  ,對於所有
,對於所有  ,必須是
,必須是  和
和  ,因為
,因為  和
和  是極限。但這是不可能的;這兩個球是分開的。因此,極限是重合的,也就是說,該序列只有一個極限。
是極限。但這是不可能的;這兩個球是分開的。因此,極限是重合的,也就是說,該序列只有一個極限。
- 如果
 ,則幾乎根據定義,我們得到
,則幾乎根據定義,我們得到  。(
。( 是距離序列)。
是距離序列)。
- 在
 中使用自然度量,級數
中使用自然度量,級數  收斂到
收斂到  。我們將其表示如下:
。我們將其表示如下:
- 任何空間,帶有離散度量。一個序列
 收斂,當且僅當它最終為常數。換句話說:
收斂,當且僅當它最終為常數。換句話說: 當且僅當,我們可以找到
當且僅當,我們可以找到 ,使得對於每個
,使得對於每個 ,
,
- 一個你可能已經知道的例子
空間 對於任何 p 範數誘導的度量,當
對於任何 p 範數誘導的度量,當 。設
。設 。並設
。並設 。
。
那麼, 當且僅當
當且僅當 。
。
如果對於任何  ,存在一個
,存在一個  使得當
使得當  和
和  都大於
都大於  時,則
時,則  對於任何
對於任何  成立,則稱函式序列
成立,則稱函式序列  在集合
在集合  上一致收斂。
上一致收斂。
定義: 如果存在一個序列  ,使得
,使得  ,則稱點
,則稱點  為集合
為集合  的一個閉包點。
的一個閉包點。
換句話說,點  是集合
是集合  的閉包點,如果存在一個在
的閉包點,如果存在一個在  中的序列收斂於
中的序列收斂於  。請注意,
。請注意, 不一定是集合
不一定是集合  的元素。
的元素。
使用球體的等效定義:點 被稱為集合
被稱為集合 的閉包點,如果對於包含
的閉包點,如果對於包含 的每一個開球
的每一個開球 ,我們都有
,我們都有 。換句話說,包含
。換句話說,包含 的每一個開球都包含
的每一個開球都包含 中至少一個不同於
中至少一個不同於 的點。
的點。
證明留作練習。
直觀地,閉包點與集合 是“無限接近”的。它非常接近,我們可以找到集合中收斂到集合的任意閉包點的序列。
是“無限接近”的。它非常接近,我們可以找到集合中收斂到集合的任意閉包點的序列。
示例:令 A 為線段 ,點
,點 不在
不在 中,但它是閉包點:令
中,但它是閉包點:令 。
。 (
( ,因此
,因此 )並且
)並且 (因為
(因為 )。
)。
定義:集合 在
在  中的閉包是所有閉包點的集合。集合A的閉包標記為
中的閉包是所有閉包點的集合。集合A的閉包標記為 或者
或者  。
。
注意  。簡單證明:對於每個
。簡單證明:對於每個  ,令
,令  。
。
對於度量空間  (直線),設
(直線),設  ,我們有
,我們有
![{\displaystyle Cl([a,b])=[a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3eddea72fcc1b24b538915dc798b35c9bf0f3fb)
![{\displaystyle Cl((a,b])=[a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd3263fd4ba19f933af00b15ad9b530b4455eef1)
![{\displaystyle Cl([a,b))=[a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f40b72d26c5687837bdeeb35c34f4d57fead95a1)
![{\displaystyle Cl((a,b))=[a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b4a77748d74b5fd1519d82516bb94536a551e4c)
定義:集合 在
在  中是閉集,如果
中是閉集,如果 。
。
含義:如果一個集合包含所有閉包點,那麼這個集合就是閉集。
等效的定義是:集合 在
在 中是閉合的,如果對於每個點
中是閉合的,如果對於每個點 ,以及對於每個球
,以及對於每個球 ,那麼
,那麼 .
.
這個定義的證明直接來自於前一個定義和收斂性的定義。
Cl 的一些基本性質(對於任何集合 )
)



 是閉合的當且僅當
是閉合的當且僅當
- 雖然以上內容暗示有限多個閉合集的並集也是一個閉合集,但這對於無限多個閉合集的並集並不一定成立。為了在實數軸上看到一個例子,令
![{\displaystyle A_{n}=\{[-1+{\frac {1}{n}},1-{\frac {1}{n}}]\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/adf2e9facb6e8ad24c28f16409da14b5b4bbede9) 。我們看到
。我們看到 無法包含它的閉包點,
無法包含它的閉包點,
因此,這個並集不能成為實數的閉合子集。
證明留給讀者作為練習。第 5 個的提示:回憶 .
.
也就是說,開集接近它的邊界但不包括它;而閉合集包含它接近的每個點。這兩個屬性可能看起來是互斥的,但它們並非如此。
- 在任何度量空間
 中,集合
中,集合 既是開集也是閉集。
既是開集也是閉集。
- 在任何具有離散度量的空間中,每個集合既是開集也是閉集。
- 在
 中,在標準度量下,唯一既是開集又是閉集的集合是
中,在標準度量下,唯一既是開集又是閉集的集合是  和
和  。但是,有些集合既不是開集也不是閉集。例如,半開區間,如
。但是,有些集合既不是開集也不是閉集。例如,半開區間,如  ,既不是開集也不是閉集。再比如,有理數集不是開集,因為圍繞一個有理數的開球包含無理數;它也不是閉集,因為存在收斂於無理數的有理數序列(例如,收斂於
,既不是開集也不是閉集。再比如,有理數集不是開集,因為圍繞一個有理數的開球包含無理數;它也不是閉集,因為存在收斂於無理數的有理數序列(例如,收斂於  的各種無窮級數)。
的各種無窮級數)。
回顧/定義:令  是空間
是空間  中的一個集合。我們定義
中的一個集合。我們定義  的補集,
的補集, 為
為  。
。
一個簡單的例子:令 ![{\displaystyle X=[0,1];A=[0,{\frac {1}{2}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75af4dbbe6e599bdd809a5d967e32f3ddafa812b) 。那麼
。那麼 ![{\displaystyle A^{c}=({\frac {1}{2}},1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8f47e141c6a629e6f8a87585a26f934671bbf47a) 。
。
一個非常重要的命題:令  是空間
是空間  中的一個集合。那麼,A 是開集當且僅當
中的一個集合。那麼,A 是開集當且僅當  是閉集。
是閉集。
證明: ( ) 首先,我們假設 A 是一個開集。我們將證明
) 首先,我們假設 A 是一個開集。我們將證明  。根據閉包的性質,我們只需要證明
。根據閉包的性質,我們只需要證明  。令
。令  (我們將證明
(我們將證明  )。
)。
對於每個球體  ,根據定義,我們有 (*)
,根據定義,我們有 (*) 。如果該點不在
。如果該點不在  中,那麼
中,那麼  。
。  是開集,因此存在一個球體
是開集,因此存在一個球體  ,使得:
,使得: ,這意味著
,這意味著  ,與 (*) 矛盾。
,與 (*) 矛盾。
( ) 另一方面,假設
) 另一方面,假設  是閉集,並證明
是閉集,並證明  是開集。設
是開集。設  為
為  中的點(我們將證明
中的點(我們將證明  )。如果
)。如果  不在
不在  中,那麼對於每個球
中,那麼對於每個球  ,都有
,都有  。這意味著
。這意味著  。根據閉包點的定義,
。根據閉包點的定義, 是
是  的閉包點,所以我們可以說
的閉包點,所以我們可以說  。
。  是閉集,因此
是閉集,因此  。這與假設
。這與假設  矛盾。
矛盾。
請注意,如前所述,集合仍然可以 **既是開集又是閉集**!
以下是一個關於  上的開集和閉集的重要定理。
上的開集和閉集的重要定理。
定理:在  中的開集
中的開集  是可數個不相交的開區間的並集。
是可數個不相交的開區間的並集。
證明:設  。設
。設  且設
且設  。存在一個開球
。存在一個開球  使得
使得  ,因為
,因為  是開的。因此,a≤x-ε 且 b≥x+ε。因此,x ∈(a,b)。集合 O 包含 (a,b) 的所有元素,因為如果一個數大於 a,小於 x,但不在 O 內,則 a 不會是 {t|t∉O, t<x} 的上確界。類似地,如果存在一個數小於 b,大於 x,但不在 O 內,則 b 不會是 {t|t∉O, t>x} 的下確界。因此,O 還包含 (a,x) 和 (x,b),所以 O 包含 (a,b)。如果 y≠x 且 y∈(a,b),則從該元素構造的區間與上述相同。如果 y<a,則 inf{t|t∉O, t>y} 也會小於 a,因為在 y 和 a 之間有一個不在 O 內的數。類似地,如果 y>b,則 sup{t|t∉O, t<y} 也會大於 b,因為在 y 和 b 之間有一個不在 O 內的數。因此,從上述過程中構造的所有可能的開區間都是不相交的。從元素 x 構造的所有此類開區間的並集就是 O,所以 O 是不相交開區間的並集。因為有理數在 R 中稠密,每個開區間內都存在一個有理數,並且因為有理數是可數的,所以開區間本身也是可數的。
是開的。因此,a≤x-ε 且 b≥x+ε。因此,x ∈(a,b)。集合 O 包含 (a,b) 的所有元素,因為如果一個數大於 a,小於 x,但不在 O 內,則 a 不會是 {t|t∉O, t<x} 的上確界。類似地,如果存在一個數小於 b,大於 x,但不在 O 內,則 b 不會是 {t|t∉O, t>x} 的下確界。因此,O 還包含 (a,x) 和 (x,b),所以 O 包含 (a,b)。如果 y≠x 且 y∈(a,b),則從該元素構造的區間與上述相同。如果 y<a,則 inf{t|t∉O, t>y} 也會小於 a,因為在 y 和 a 之間有一個不在 O 內的數。類似地,如果 y>b,則 sup{t|t∉O, t<y} 也會大於 b,因為在 y 和 b 之間有一個不在 O 內的數。因此,從上述過程中構造的所有可能的開區間都是不相交的。從元素 x 構造的所有此類開區間的並集就是 O,所以 O 是不相交開區間的並集。因為有理數在 R 中稠密,每個開區間內都存在一個有理數,並且因為有理數是可數的,所以開區間本身也是可數的。
- 在任何度量空間中,單點集
 是閉集。要了解原因,請考慮開集
是閉集。要了解原因,請考慮開集  。令
。令  。那麼
。那麼  ,所以
,所以  。令
。令  。那麼
。那麼  。所以
。所以  是開集,因此
是開集,因此  是閉集。
是閉集。
- 在任何度量空間中,每個有限集
 是閉集。要了解原因,請觀察
是閉集。要了解原因,請觀察 ![{\displaystyle T^{c}={\Big [}\bigcup \{x_{i}\}{\Big ]}^{c}=\bigcap \{x_{i}\}^{c}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8f52781672e933ec9a82a7eade5bb4f87a5175d2) 是開集,所以
是開集,所以  是閉集。
是閉集。
- 閉區間 [a,b] 是閉集。
- 康託集 考慮區間 [0,1] 並將其稱為 C0。令 A1 等於 {0,
 } 並令 dn =
} 並令 dn =  。令 An+1 等於集合 An∪{x|x=a+2dn, a∈An}。令 Cn 為
。令 An+1 等於集合 An∪{x|x=a+2dn, a∈An}。令 Cn 為  {[a,a+dn]},這是閉集的有限並集,因此是閉集。那麼交集
{[a,a+dn]},這是閉集的有限並集,因此是閉集。那麼交集  稱為康託集,是閉集。
稱為康託集,是閉集。
- 證明一個點 x 在 X 內有收斂於 x 的點序列當且僅當包含 x 的所有球都包含 X 內的至少一個元素。
- 在
 中,唯一既是開集又是閉集的集合是空集和整個集合。 然而,當考慮
中,唯一既是開集又是閉集的集合是空集和整個集合。 然而,當考慮  時,情況就不一樣了。 請舉出一個在
時,情況就不一樣了。 請舉出一個在  中既是開集又是閉集的集合。
中既是開集又是閉集的集合。
- 設
 是空間
是空間  中的一個集合。 證明以下結論:
中的一個集合。 證明以下結論:

讓我們回顧一下函式連續性的概念。 從直觀上來說,連續性意味著你可以在紙上畫一個函式,而不用提起筆。 連續性在拓撲學中很重要。 但讓我們從頭開始。
經典的 delta-epsilon 定義: 設  是空間。 函式
是空間。 函式  在點
在點  處連續,如果對於所有
處連續,如果對於所有  都存在一個
都存在一個  ,使得:對於所有滿足
,使得:對於所有滿足  的
的  ,我們有
,我們有  。
。
讓我們用球來重新定義:一個函式 在點
在點 處連續,如果對於所有
處連續,如果對於所有 都存在
都存在 ,使得以下成立:對於所有滿足
,使得以下成立:對於所有滿足 的
的 ,都有
,都有 。或者更簡單地說:
。或者更簡單地說:
看起來好多了!但我們還可以做得更好。
定義
- 如果一個函式在集合 S 中的每個點處都連續,那麼該函式在集合 S 中是連續的。
- 如果一個函式在其整個定義域上都是連續的,那麼該函式是連續的。
命題: 函式  是連續的,根據以上定義
是連續的,根據以上定義  對
對  中的每個開集
中的每個開集  ,
, 的逆像,
的逆像,  ,在
,在  中是開的。也就是說,
中是開的。也就是說, 中每個開集的逆像在
中每個開集的逆像在  中是開的。
中是開的。
注意, 不必是滿射或雙射才能使
不必是滿射或雙射才能使  有定義。符號
有定義。符號  僅僅表示
僅僅表示  .
.
證明: 首先,假設函式  根據定義是連續的(
根據定義是連續的( 方向)。我們需要證明對於每個開集
方向)。我們需要證明對於每個開集  ,
, 是開的。
是開的。
設  是一個開集。設
是一個開集。設  。
。  在
在  中,因為
中,因為  是開集,我們可以找到
是開集,我們可以找到  ,使得
,使得  。因為 f 是連續函式,對於這個
。因為 f 是連續函式,對於這個  ,我們可以找到一個
,我們可以找到一個  使得
使得  。這意味著
。這意味著  ,因此,
,因此, 是內點。這對所有
是內點。這對所有  都成立 - 意味著
都成立 - 意味著  中的所有點都是內點,根據定義,
中的所有點都是內點,根據定義, 是開集。
是開集。
( )另一方面,假設對於一個函式
)另一方面,假設對於一個函式 ,對於每個開集
,對於每個開集 ,
, 在
在 中是開集。我們需要證明
中是開集。我們需要證明 是連續的。
是連續的。
對於每個 以及對於每個
以及對於每個 ,集合
,集合 在
在 中是開集。因此集合
中是開集。因此集合 在
在 中是開集。注意
中是開集。注意 。因為
。因為 是開集,這意味著我們可以找到一個
是開集,這意味著我們可以找到一個 ,使得
,使得 ,並且我們有
,並且我們有 .
.
最後一個證明給了我們一個額外的定義,我們將用於本書剩餘部分的連續性。這個新定義的優點是它只使用開集,因此可以應用於沒有度量的空間,所以我們現在有了兩個等價的定義,可以用來定義連續性。
- 設
 是從任何空間
是從任何空間  到任何空間
到任何空間  的任何函式,其中
的任何函式,其中  是離散度量。那麼
是離散度量。那麼  是連續的。為什麼?對於每個開集
是連續的。為什麼?對於每個開集  ,集合
,集合  是開的,因為在具有離散度量的空間中,每個集合都是開的。
是開的,因為在具有離散度量的空間中,每個集合都是開的。
- 設
 為恆等函式。
為恆等函式。  是連續的:每個開集的源都是它本身,因此是開的。
是連續的:每個開集的源都是它本身,因此是開的。
- 證明函式
 是連續的
是連續的  對於
對於  中的每個閉集
中的每個閉集  ,
, 的逆像,
的逆像, ,在
,在  中是閉的。
中是閉的。
在度量空間 X 中,從 X 到度量空間 Y 的函式 **一致連續** ,如果對於所有  ,都存在一個
,都存在一個  ,使得對於所有
,使得對於所有  ,
, 意味著
意味著  。
。
等距是一個 滿射 對映  ,其中
,其中  和
和  是度量空間,並且對於所有
是度量空間,並且對於所有  ,
, 。
。
在這種情況下, 和
和  被稱為等距。
被稱為等距。
請注意, 的 單射性 來自於保持距離的性質
的 單射性 來自於保持距離的性質




因此,等距必然是 雙射。
- 證明一個集合是度量開集 當且僅當 它是一個(可能無限的)開球的並集。
- 證明離散度量實際上是一個度量。






























































![{\displaystyle B_{1}{\bigl (}(0,0){\bigr )}={\Big \{}(x,y)\in \mathbb {R} ^{2}:d{\bigl (}(x,y),(0,0){\bigr )}<1{\Big \}}={\Big \{}(x,y):{\bigl \|}(x,y)-(0,0){\bigr \|}_{p}<1{\Big \}}={\Big \{}(x,y):\|(x,y)\|_{p}<1{\Big \}}={\Big \{}(x,y):{\sqrt[{p}]{|x|^{p}+|y|^{p}}}<1{\Big \}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b8ebf9c0bf5f2d66d2fe08844d3548e60e3a9868)

































![{\displaystyle int([a,b])=(a,b)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd3d977333a969ec5d8d06a91b7021d52842188f)
![{\displaystyle int((a,b])=(a,b)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bfed9af226d984832f234c50d6da2f32e3142aed)










![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)
![{\displaystyle B_{\epsilon }(a)\subset [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b62496930755059267ae3e9c396cba3aca37dd0)




































































































![{\displaystyle Cl([a,b])=[a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3eddea72fcc1b24b538915dc798b35c9bf0f3fb)
![{\displaystyle Cl((a,b])=[a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd3263fd4ba19f933af00b15ad9b530b4455eef1)
![{\displaystyle Cl([a,b))=[a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f40b72d26c5687837bdeeb35c34f4d57fead95a1)
![{\displaystyle Cl((a,b))=[a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b4a77748d74b5fd1519d82516bb94536a551e4c)








![{\displaystyle A_{n}=\{[-1+{\frac {1}{n}},1-{\frac {1}{n}}]\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/adf2e9facb6e8ad24c28f16409da14b5b4bbede9)








![{\displaystyle X=[0,1];A=[0,{\frac {1}{2}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75af4dbbe6e599bdd809a5d967e32f3ddafa812b)
![{\displaystyle A^{c}=({\frac {1}{2}},1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8f47e141c6a629e6f8a87585a26f934671bbf47a)



























![{\displaystyle T^{c}={\Big [}\bigcup \{x_{i}\}{\Big ]}^{c}=\bigcap \{x_{i}\}^{c}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8f52781672e933ec9a82a7eade5bb4f87a5175d2)




















































