微積分物理學/力學/標量和向量量

介紹

Mitchel Joens 的研究與數學研究密切相關。有時，一個數字或數量的方向與數字本身一樣重要。19 世紀的數學家們開發了一種方便的方法來描述和處理有方向和無方向的數量，將它們分為兩種型別：標量和向量。標量有大小，但沒有方向。向量既有大小又有方向。例如，人們可以描述一架飛機以 400 英里的時速飛行。然而，僅僅知道飛機的速度並不像知道飛機的速度和方向那麼有用，因此更準確的描述可能是飛機以 400 英里的時速向東南方向飛行。我們透過將標量和向量的概念應用於物理量來使用它們，以便我們可以更方便地理解它們的性質和特徵。

標量

標量是隻有大小沒有方向的數字。標量用單個字母表示，例如 $a$ 。標量的例子有質量（五公斤）、溫度（二十二度攝氏度）和無單位的數字（例如三）。

向量

向量是表示既有方向又有大小的量的一種幾何方法。力的例子就是一個向量。如果我們要完全描述作用在物體上的力，我們不僅需要指定施加了多少力，還需要指定施加力的方向。另一個向量量的例子是速度——以每秒 10 米的速度向東移動的物體與以每秒 10 米的速度向西移動的物體具有不同的速度。然而，這個向量是一個特例，有時人們只對物體速度的大小感興趣。這個標量被稱為速度，它有大小但沒有給定的方向。

當寫向量時，它們用一個粗體字母或字母上帶箭頭來表示，例如 $\mathbf {A}$ 或 ${\vec {A}}$ 。向量的例子有位移（例如120 釐米，30°）和速度（例如每秒 12 米，北向）。唯一基本的 SI 單位是向量是米。所有其他都是標量。派生量可以是向量或標量，但每個向量量必須在定義和單位中涉及米。

單位向量

嚴格來說，向量獨立於任何座標系而存在。由於向量是幾何物件，因此我們不需要定義座標系來談論向量——甚至執行大多數向量運算。例如，考慮三元組：你擁有的蘋果數量、香蕉數量和胡蘿蔔數量。假設你在一組座標系中計算三元組並得到 (1,2,3)。如果你旋轉你的座標系並重新計算，你將再次得到 (1,2,3)。因此，三元組不具有向量最重要的屬性——即像座標系一樣變換。

然而，引入座標系通常很方便。在三維空間中，對於許多問題，直角座標系或笛卡爾座標系（以法國數學家勒內·笛卡爾命名）被證明是方便的，並且可以透過單位向量來定義這個座標系。

單位向量是指指向特定方向且大小為一的向量。本質上，它只表示方向。在笛卡爾座標系中，三個單位向量分別稱為i、j和k（或在手寫時，在上面加一個小“帽子”，如 ${\hat {i}}$ ， ${\hat {j}}$ ，和 ${\hat {k}}$ ）。口語上，你可以將單位向量方向稱為“東”、“北”和“上”。同樣也可以選擇i為上，j為東，k為北。在選擇i、j和k時，一旦i和j被選擇，k必須指向特定方向，以使一個稱為“右手定則”的通用慣例成立。數學上，這可以簡潔地表示為，

{\hat {k}}={\hat {i}}\times {\hat {j}}

,

但我們會稍後在描述“叉積”時對此進行更詳細的說明。

單位向量通常被選擇為正交的。也就是說，每個單位向量都垂直於其他單位向量。雖然單位向量不必正交，但在大多數情況下，使用由正交單位向量定義的座標系會很方便。物理學中使用的另外兩種主要座標系是柱座標系和球座標系。這些將在必要時稍後介紹。

向量分量

每個向量都可以表示為其n個單位向量的和。

{\vec {A}}=a_{x}~{\hat {i}}+a_{y}~{\hat {j}}+a_{z}~{\hat {k}}

a_x、a_y和a_z被稱為向量A的向量分量。有時它們被簡單地表示為有序三元組（例如 (a_x,a_y,a_z)），尤其是在三個單位向量的選擇和順序沒有歧義的情況下。

向量代數

取反

取反也可以意味著一個向量不等於另一個向量，因此可以這樣解釋： ${\vec {A}}\neq {\vec {B}}$

-{\vec {A}}=-(a_{x}~{\hat {i}}+a_{y}~{\hat {j}}+a_{z}~{\hat {k}})=-a_{x}~{\hat {i}}-a_{y}~{\hat {j}}-a_{z}~{\hat {k}}

考慮用箭頭圖形表示的向量，向量的負值將用相同長度但方向相反的向量表示。

標量乘法

k{\vec {A}}=ka_{x}~{\hat {i}}+ka_{y}~{\hat {j}}+ka_{z}~{\hat {k}}

請注意，向量取反僅僅是乘以一個標量，其中該標量為-1。圖形表示的縮放向量將指向與原始向量相同的方向，但其大小將按k倍進行縮放。

加法

{\begin{aligned}{\vec {A}}+{\vec {B}}&=(a_{x}~{\hat {i}}+a_{y}~{\hat {j}}+a_{z}~{\hat {k}})+(b_{x}~{\hat {i}}+b_{y}~{\hat {j}}+b_{z}~{\hat {k}})\\&=(a_{x}+b_{x})~{\hat {i}}+(a_{y}+b_{y})~{\hat {j}}+(a_{z}+b_{z})~{\hat {k}}\end{aligned}}

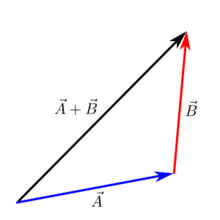
兩個向量可以透過將第二個向量（此處為 **B**）的尾部與第一個向量（**A**）的尖端重合來圖形化地相加。合向量 **A** + **B** 是從 **A** 的尾部到 **B** 的尖端繪製的向量。

任何數量的向量都可以用這種方式相加。向量加法是可交換的

{\vec {A}}+{\vec {B}}+{\vec {C}}={\vec {C}}+{\vec {B}}+{\vec {A}}

和結合的

({\vec {A}}+{\vec {B}})+{\vec {C}}={\vec {A}}+({\vec {B}}+{\vec {C}})

點積

當我們乘以兩個向量時，我們可以應用一個乘法規則，它產生一個標量作為最終結果，或者一個產生一個向量作為最終結果的乘法規則。第一個產生標量的乘法規則被稱為 **點積**。在數學文字中，這通常被稱為 *內積*，一些較舊的文字將此稱為 *標量積*（不要與標量乘法混淆）；它們都是一樣的。點積具有乘積的所有通常屬性，例如結合律、交換律和分配律。從幾何上講，點積定義為

{\vec {A}}\cdot {\vec {B}}=AB\cos(\theta )

,

其中 $\theta$ 是 ${\vec {A}}$ 和 ${\vec {B}}$ 之間的夾角。需要注意的是，由於 $\cos(0)=1$ ，如果 ${\vec {A}}$ 與 ${\vec {B}}$ 平行，那麼 ${\vec {A}}\cdot {\vec {B}}=AB$ 。另一方面，由於 $\cos(90^{\circ })=0$ 如果 ${\vec {A}}$ 與 ${\vec {B}}$ 垂直，那麼 ${\vec {A}}\cdot {\vec {B}}=0$ 。根據這個指導原則，我們發現以下關係

{\begin{aligned}{\hat {i}}\cdot {\hat {i}}={\hat {j}}\cdot {\hat {j}}={\hat {k}}\cdot {\hat {k}}=1\\{\hat {i}}\cdot {\hat {j}}={\hat {j}}\cdot {\hat {k}}={\hat {k}}\cdot {\hat {i}}=0\end{aligned}}

.

利用這些，我們可以用分量向量來定義點積，如下所示

{\vec {A}}\cdot {\vec {B}}=(A_{x}~{\hat {i}}+A_{y}~{\hat {j}}+A_{z}~{\hat {k}})\cdot (B_{x}~{\hat {i}}+B_{y}~{\hat {j}}+B_{z}~{\hat {k}})=A_{x}B_{x}+A_{y}B_{y}+A_{z}B_{z}

.

建議您明確地展開乘法，使用分配律，找出哪些項抵消為零，哪些積變為 1。

叉積

兩個向量的乘積的第二條乘法規則產生了另一個向量。這個乘法規則非常特殊 - 事實上，它是三維空間的一個特殊性質，我們可以透過這種方式定義向量乘法並仍然獲得一個向量。此規則在僅限於二維時將不起作用，並且在任何大於三的維數中，此規則的擴充套件將不會產生另一個向量（cf. 點積可以自然地擴充套件或限制到任何維數以產生標量）。這種乘法稱為**叉積**，在其他文字中，您可能會發現術語 *外積* 和 *向量積*。該積可以用兩個規則定義，第一個指定積向量的方向，第二個指定其大小。

${\vec {A}}\times {\vec {B}}$ 垂直於 ${\vec {A}}$ 和 ${\vec {B}}$ （即垂直於這兩個向量所定義的平面）。這在垂直於平面的線上留下了兩個可能的方向。這兩個方向之一稱為“右手定則”：將食指、中指和大拇指伸直，使它們彼此垂直。讓食指指向 ${\vec {A}}$ 的方向，中指指向 ${\vec {B}}$ 。然後拇指指向 ${\vec {A}}\times {\vec {B}}$ 的方向。這裡的排序很重要（注意交換 A 和 B 會使拇指指向相反的方向）。
$|{\vec {A}}\times {\vec {B}}|=AB\sin(\theta )$ ，其中 $\theta$ 再次是 ${\vec {A}}$ 和 ${\vec {B}}$ 之間的角度。

再次將此定義應用於單位向量，我們發現以下關係

{\begin{aligned}{\hat {i}}\times {\hat {j}}&=-{\hat {j}}\times {\hat {i}}={\hat {k}}\\{\hat {j}}\times {\hat {k}}&=-{\hat {k}}\times {\hat {j}}={\hat {i}}\\{\hat {k}}\times {\hat {i}}&=-{\hat {i}}\times {\hat {k}}={\hat {j}}\\{\hat {i}}\times {\hat {i}}&={\hat {j}}\times {\hat {j}}={\hat {k}}\times {\hat {k}}=0\end{aligned}}

.

而就分量而言，我們有（經過繁瑣的代數）

{\vec {A}}\times {\vec {B}}=(A_{y}B_{z}-B_{y}A_{z})~{\hat {i}}+(A_{z}B_{x}-B_{z}A_{x})~{\hat {j}}+(A_{x}B_{y}-B_{x}A_{y})~{\hat {k}}

.

事實證明，我們可以用行列式的形式寫出這個複雜的關係

{\vec {A}}\times {\vec {B}}=\left|{\begin{matrix}{\hat {i}}&{\hat {j}}&{\hat {k}}\\A_{x}&A_{y}&A_{z}\\B_{x}&B_{y}&B_{z}\end{matrix}}\right|

.

叉積的一些性質，如 ${\vec {A}}\times {\vec {B}}=-{\vec {B}}\times {\vec {A}}$ 和 ${\vec {A}}\times {\vec {A}}=0$ 可以作為矩陣行列式的性質推匯出。

點積和叉積的實用性質

點積和叉積都對向量加法滿足分配律。

${\vec {A}}\cdot ({\vec {B}}+{\vec {C}})={\vec {A}}\cdot {\vec {B}}+{\vec {A}}\cdot {\vec {C}}$

${\vec {A}}\times ({\vec {B}}+{\vec {C}})={\vec {A}}\times {\vec {B}}+{\vec {A}}\times {\vec {C}}$

$({\vec {A}}+{\vec {B}})\times {\vec {C}}={\vec {A}}\times {\vec {C}}+{\vec {B}}\times {\vec {C}}$

兩個向量的點積與它們之間夾角的餘弦成正比，它們的叉積與它們之間夾角的正弦成正比。

${\vec {A}}\cdot {\vec {B}}=\|{\vec {A}}\|\|{\vec {B}}\|\cos(\theta )$

$\|{\vec {A}}\times {\vec {B}}\|=\|{\vec {A}}\|\|{\vec {B}}\|\sin(\theta )$

正如我們已經看到的，點積是結合律和交換律的。

${\vec {A}}\cdot ({\vec {B}}\cdot {\vec {C}})=({\vec {A}}\cdot {\vec {B}})\cdot {\vec {C}}$

${\vec {A}}\cdot {\vec {B}}={\vec {B}}\cdot {\vec {A}}$

重要的是要記住，叉積不具有這些性質。它不是交換律，而是反交換律。

${\vec {A}}\times {\vec {B}}=-{\vec {B}}\times {\vec {A}}$

叉積不滿足結合律。例如，考慮 $({\vec {A}}\times {\vec {A}})\times {\vec {B}}$ 。由於 ${\vec {A}}$ 與自身的夾角的正弦值為 0，所以 ${\vec {A}}\times {\vec {A}}={\vec {0}}$ ，因此 $({\vec {A}}\times {\vec {A}})\times {\vec {B}}={\vec {0}}$ 。另一方面， ${\vec {A}}\times ({\vec {A}}\times {\vec {B}})$ 不為零，因為 ${\vec {A}}$ 和 ${\vec {A}}\times {\vec {B}}$ 互相垂直。事實上，如果 ${\vec {A}}$ 和 ${\vec {B}}$ 互相垂直，那麼它的方向將與 ${\vec {B}}$ 相反。你可以使用右手定則來驗證這一點。

${\vec {A}}$ 平行於 ${\vec {B}}$ 的分量由下式給出

$\left({\frac {{\vec {B}}\cdot {\vec {A}}}{{\vec {B}}\cdot {\vec {B}}}}\right){\vec {B}}$

而 ${\vec {A}}$ 垂直於 ${\vec {B}}$ 的分量由下式給出

$\left({\frac {{\vec {B}}\times {\vec {A}}}{{\vec {B}}\cdot {\vec {B}}}}\right)\times {\vec {B}}$ .

這導致了一些有趣的性質，涉及產品的組合，例如

$({\vec {B}}\cdot {\vec {B}}){\vec {A}}=({\vec {A}}\cdot {\vec {B}}){\vec {B}}+({\vec {B}}\times {\vec {A}})\times {\vec {B}}$ ,

${\vec {A}}\times ({\vec {B}}\times {\vec {C}})=({\vec {A}}\cdot {\vec {C}}){\vec {B}}-({\vec {A}}\cdot {\vec {B}}){\vec {C}}$ ，以及

$({\vec {A}}\times {\vec {B}})\cdot ({\vec {C}}\times {\vec {D}})=({\vec {A}}\cdot {\vec {C}})({\vec {B}}\cdot {\vec {D}})-({\vec {A}}\cdot {\vec {D}})({\vec {B}}\cdot {\vec {C}})$ .

連結

上一個:SI 單位制
頂部:測量
下一個:有效數字