訊號與系統/二階傳遞函式

二階傳遞函式是最簡單的具有復極點的傳遞函式。對其進行分析可以回顧我們從模擬濾波器設計中獲得的資訊，併為實現二階段級聯濾波器提供一個良好的起點。

全極點二階傳遞函式

傳遞函式

連續時間全極點二階系統的傳遞函式為

H(s)={\frac {b_{0}}{s^{2}+a_{1}s+a_{0}}}

請注意， $s^{2}$ 的係數已設為 1。這在不損失一般性的情況下簡化了書寫，因為分子和分母可以乘以或除以相同的因子。

對於 $s=i\omega$ ，其頻率響應具有直流幅度

H(i\omega =0)={\frac {b_{0}}{a_{0}}}

對於非常高的頻率，分母中最重要的項是 $(i\omega )^{2}$ ，頻率響應越來越接近

H(i\omega )\cong {\frac {b_{0}}{(i\omega )^{2}}}

在高頻下，幅頻響應線上性圖中看起來像一個（平方）雙曲線，在對數-對數圖中看起來像一條具有負斜率的直線。將頻率繪製在十年制中，幅度繪製在分貝中，則顯示出 -40 [dB/十年] 的斜率。

在直流具有給定幅度，而在高頻下幅度接近於零，表明傳遞函式是低通型別的。

極點

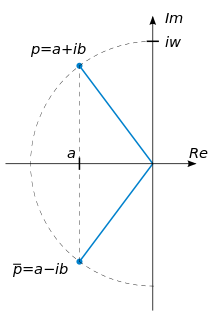
系統的極點由分母多項式的根給出

p,p^{*}={\frac {-a_{1}\pm {\sqrt {a_{1}^{2}-4a_{0}}}}{2}}

如果平方根內的項為負數，則極點為複共軛。這是濾波器設計中的普遍情況：人們對具有兩個實極點的二階傳遞函式沒有太大的興趣。

根據極點的位置，傳遞函式可以被重寫為

H(s)={\frac {k}{(s-p)(s-p^{*})}}={\frac {k}{s^{2}-2Re(p)s+abs(p)^{2}}}

極點的幅度決定了濾波器的截止頻率。截止頻率定義為對數-對數幅頻響應曲線中水平線和 -40 [dB/decade] 線相交點的橫座標。注意，這並不一定是濾波器的 -3 [dB] 衰減頻率。

\omega _{0}=abs(p)={\sqrt {a_{0}}}

極點的實部與截止頻率之比與系統的阻尼比成正比，或與系統的品質因數成反比。

\zeta ={\frac {-Re(p)}{\omega _{0}}}={\frac {a_{1}}{2\omega _{0}}}

Q={\frac {1}{2\zeta }}={\frac {\omega _{0}}{-2Re(p)}}={\frac {\omega _{0}}{a_{1}}}

極點越靠近虛軸，在小於但接近系統截止頻率的頻率處就越可能出現諧振。

傳遞函式重寫

利用這些，直流增益為 1 的傳遞函式可以根據截止頻率和阻尼比重寫為以下形式

H(s)={\frac {\omega _{0}^{2}}{s^{2}+2\zeta \omega _{0}\cdot s+\omega _{0}^{2}}}

$s$ 和 $\omega _{0}$ 的單位均為 [s^-1]。 $\zeta$ 的單位為 [1]，總傳遞函式的單位也是 [1]。

雙二次二階傳遞函式

傳遞函式

名稱“雙二次”源於該函式具有兩個二階多項式。

H(s)={\frac {b_{2}s^{2}+b_{1}s+b_{0}}{s^{2}+a_{1}s+a_{0}}}

極點

極點的分析方式與全極點二階傳遞函式相同。它們決定了系統的截止頻率和品質因數。

零點

零點用於影響幅頻響應的形狀。

將零點放在略高於截止頻率的虛軸上，可以在阻帶中獲得更大的衰減，並使通帶到阻帶的過渡更快。這就是切比雪夫 II 型和橢圓濾波器函式的工作原理。
將零點精確地放在虛軸上的截止頻率處，會迫使該特定點的幅度為零。這對應於帶阻（或陷波）函式。
將單個零點放在 s 平面的 (0, 0) 座標處會將函式轉換為帶通函式。可以透過將係數 $b_{2}=0$ 和 $b_{0}=0$ 來實現。
將兩個零點都放在 (0, 0) 座標處，將函式轉換為高通函式。這可以透過設定係數 $b_{1}=0$ 和 $b_{0}=0$ 來實現。
將零點放在右半平面，關於極點對稱，得到一個全通函式：虛軸上的任何點到零點和到相應極點的距離都相等。這個全通函式用於整形傳遞函式的相位響應。

示例

6階歸一化巴特沃斯濾波器

示例

本例分析了 6 階歸一化巴特沃斯濾波器的 3 個二階部分。

巴特沃斯濾波器的極點在以複平面原點為中心的圓的左半部分上均勻分佈。每個複共軛極點對構成一個二階全極點傳遞函式。這些二階函式的乘積得到了 6 階巴特沃斯傳遞函式。

極點對

在側面的圖形中，極點 $p_{1}$ 及其複共軛極點距離虛軸很近。它們的幅頻響應將在拐角頻率處出現過沖。這對應於欠阻尼情況，並且二階部分將在接近拐角頻率的頻率處表現出一些共振。

極點 $p_{2}$ 及其複共軛極點相對於虛軸的夾角為 45°。它們的幅頻響應將在拐角頻率處出現 3 dB 的衰減。這是幅頻響應不出現過沖的臨界情況。然而，這並不對應於臨界阻尼情況：階躍響應在穩定之前會出現過沖。

極點 $p_{3}$ 及其複共軛極點距離虛軸很遠。它們的幅頻響應將在拐角頻率處出現較大的衰減。這對應於過阻尼情況。

幅頻響應

以下 Octave 程式碼允許繪製各個二階部分的幅頻響應以及全域性巴特沃斯幅頻響應。

#-------------------------------------------------------------------------------
# Specifications
#
order = 6;
pointNb = 100;
wLog = logspace(-1, 1, pointNb);
AdbMax = 10;
AdbMin = -40;

#-------------------------------------------------------------------------------
# Butterworth filter
#
[num, den] = butter(order, 1, 's');
while ( length(num) < length(den) )
  num = [0, num];
endwhile;

#-------------------------------------------------------------------------------
# Normalized filter, transfer functions plot
#
Adb = 20*log10(abs(freqs(num, den, wLog)));

figure(2);
semilogx(wLog, Adb);
hold on;
for index = 1:order
  if imag(poles(index)) > 0
    num = [0, 0, 1];
    den = [1, -2*real(poles(index)), abs(poles(index))^2];
    Adb = 20*log10(abs(freqs(num, den, wLog)));
    semilogx(wLog, Adb, 'g');
  endif
endfor
hold off;

axis([wLog(1), wLog(length(wLog)), AdbMin, AdbMax]);
xlabel('Frequency');
ylabel('Amplitude responses');
grid;

側面藍色曲線顯示全域性幅頻響應。

綠色曲線是各個二階部分的響應。它們都具有一個水平漸近線趨向於直流。它們也都有一個高頻 -40 dB/decade 的漸近線。這兩個漸近線在點 ( $\omega =1$ [s^-1], $A=0$ [dB]) 相交。拐角頻率位於 $\omega =1$ [s^-1] 或 $f=1/{(2\pi )}$ [Hz]

高 Q 值二階函式

頂部的綠色幅頻響應顯示了高品質因數響應的樣子。它在略低於拐角頻率的頻率處有一個超過 0 dB（此處為 6.02 dB）的峰值。在拐角頻率處，幅度已經下降（此處為 5.68 dB）。

最大平坦二階函式

中間的綠色幅頻響應顯示了最大平坦響應的樣子。它在拐角頻率處具有 -3.02 dB 的幅度。

無論階數如何，巴特沃斯函式在拐角頻率處都表現出相同的 -3.02 dB 衰減。

低 Q 值二階函式

底部的綠色幅頻響應顯示了低品質因數響應的樣子。它在拐角頻率處具有小於 -3 dB（此處為 -5.72 dB）的幅度。