卡諾迴圈描述了熱量轉化為能量的熱力學迴圈。該迴圈遵循四個可逆步驟:(1)等溫膨脹,(2)絕熱膨脹,(3)等溫壓縮和(4)絕熱壓縮。由於迴圈的兩個特性,即可逆性和在最熱儲層和最冷儲層之間進行最大可能的熱量傳遞,因此可以實現正淨功。這在下圖和表格中顯示。
 卡諾迴圈及其儲層的圖片
卡諾迴圈及其儲層的圖片
 卡諾迴圈的P-T圖
卡諾迴圈的P-T圖
根據該圖,熱量從熱儲層T(1)轉移到發動機,由Q(1)表示。Q(1)和Q(2)的符號相反,因為熱機的效率是進入系統的總熱量減去離開系統的總熱量。
對於右側的圖,熱機的P-T圖顯示,總功是頂部曲線面積和底部曲線面積之間的差。它還表明,根據熱力學第二定律,熱機的熱量傳遞效率不可能達到100%。以下公式顯示了熱機效率,該公式用於推匯出自發性的第二定律。

也可以用兩種其他方式表示
 或
或 
卡諾迴圈的P-T圖可以根據下表分為四個步驟。從步驟1到步驟2,存在等溫膨脹,這意味著內能 等於零。這使得q = -w,可以計算第一次等溫膨脹的工作量。隨後,存在絕熱膨脹,其中熱量傳遞q等於零,表明
等於零。這使得q = -w,可以計算第一次等溫膨脹的工作量。隨後,存在絕熱膨脹,其中熱量傳遞q等於零,表明 ,而從步驟2到步驟3再到步驟4,分別存在等溫膨脹和絕熱膨脹。方程式顯示在表格中。
,而從步驟2到步驟3再到步驟4,分別存在等溫膨脹和絕熱膨脹。方程式顯示在表格中。
 卡諾迴圈表
卡諾迴圈表
來源:Castellan,Gilbert W. 物理化學。第3版。門洛帕克:Addison-Wesley P C,1983。
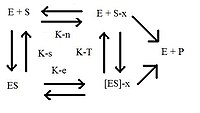 酶及其底物的熱力學迴圈。新增的字尾-x表示該分子處於其過渡態
酶及其底物的熱力學迴圈。新增的字尾-x表示該分子處於其過渡態
根據過渡態理論,酶是靈活的蛋白質分子,可以催化經歷初始構象和最終構象之間過渡態階段的分子。底物的過渡態或“半椅”構象比基態或最終態與酶的反應性更高(有關更多詳細資訊,請參閱過渡態)。這種最新的理論被稱為過渡態穩定化。使用X射線晶體學和誘變方法或酶的氨基酸的改變,有助於獲得更多關於過渡態穩定化的知識。
該理論基於兩個假設,即反應受到動態瓶頸的限制,並且該反應處於平衡狀態。該理論的一般公式為

其中k是反應速率常數, 是傳遞係數,
是傳遞係數, 是頻率,以及
是頻率,以及
 是平衡常數。常數
是平衡常數。常數 只是影響反應速率的無關因素的校正因子。
只是影響反應速率的無關因素的校正因子。
使用所示的圖,比較酶和酶過渡態的兩個反應速率。

其中下標 e 和 n 分別代表酶促和非酶促活性。由於  等同於最簡單形式的催化速率常數
等同於最簡單形式的催化速率常數  ,該方程式可以用解離常數
,該方程式可以用解離常數  和過渡態常數
和過渡態常數  表示為
表示為

由於酶促反應速率很大,因此比例  通常為
通常為  到
到  。比例
。比例  可以從方程中去掉,因為它不太可能使酶與非酶速率反應的偏差很大。因此,最終的方程式推導為
可以從方程中去掉,因為它不太可能使酶與非酶速率反應的偏差很大。因此,最終的方程式推導為

表明過渡態的結合能力大於基態底物。
Kraut, Joseph. “酶是如何起作用的?” 研究文章。加州大學聖地亞哥分校教授。發表於 1988 年 10 月。
























