量子世界/影響和應用/量子彈跳球

量子彈跳球

作為一個具體的例子，考慮以下勢能

$V(z)=mgz\quad {\hbox{if}}\quad z>0\quad {\hbox{and}}\quad V(z)=\infty \quad {\hbox{if}}\quad z<0.$

$g$ 是地板上的重力加速度。對於 $z<0,$，薛定諤方程如 上一節 所示，告訴我們 $d^{2}\psi (z)/dz^{2}=\infty$ 除非 $\psi (z)=0.$ 因此，對於負的 $z$，唯一合理的解是 $\psi (z)=0.$ 要求 $V(z)=\infty$ 對於 $z<0$ 確保了我們的完美彈性、無摩擦的量子彈跳器不會被發現在地板以下。

由於一圖勝千言，我們不會為這個特定的勢能求解時間無關薛定諤方程，而是簡單地繪製其前八個解

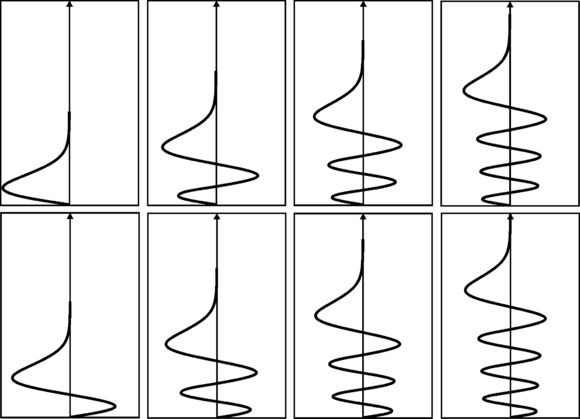
在相同的勢能下，經典的彈跳球會在哪裡改變其運動方向？觀察位置和動量（波數）之間的相關性。

所有這些狀態都是穩態的；在 $z$ 軸的任何特定區間內找到量子彈跳器的機率與時間無關。那麼我們如何讓它運動呢？

回想一下，薛定諤方程的任何線性組合都是另一個解。考慮兩個穩態的這種線性組合

$\psi (t,x)=A\,\psi _{1}(x)\,e^{-i\omega _{1}t}+B\,\psi _{2}(x)\,e^{-i\omega _{2}t}.$

假設係數 $A,B$ 和波函式 $\psi _{1}(x),\psi _{2}(x)$ 是實數，我們計算與 $\psi (t,x)$ 相關的粒子的平均位置。

$\int \!dx\,\psi ^{*}x\psi =\int \!dx\,(A\psi _{1}e^{i\omega _{1}t}+B\psi _{2}e^{i\omega _{2}t})\,x\,(A\psi _{1}e^{-i\omega _{1}t}+B\psi _{2}e^{-i\omega _{2}t})$

$=A^{2}\int \!dx\,\psi _{1}^{2}\,x+B^{2}\int \!dx\,\psi _{2}^{2}\,x+AB(e^{i(\omega _{1}-\omega _{2})t}+e^{i(\omega _{2}-\omega _{1})t})\int \!dx\,\psi _{1}x\psi _{2}.$

前兩個積分分別是與 $\psi _{1}(x)\,e^{i\omega _{1}t}$ 和 $\psi _{2}(x)\,e^{i\omega _{2}t},$ 相關的粒子的（與時間無關的）平均位置。最後一項等於

$2AB\cos(\Delta \omega \,t)\int \!dx\,\psi _{1}x\psi _{2},$

這告訴我們粒子的平均位置以頻率 $\Delta \omega =\omega _{2}-\omega _{1}$ 和振幅 $2AB\int \!dx\,\psi _{1}x\psi _{2}$ 在前兩項的總和附近振盪。

訪問 此網站 以觀看與最初與高斯分佈相關的量子彈跳球相關的機率分佈的時間依賴性。