當沒有抵消吸引力(如原子氫中原子核和電子之間的吸引力)時,我們將計算位置機率分佈的模糊度隨著相應動量模糊度的增加而增加的速率。
由於易於處理,我們選擇一個高斯函式

它有一個鐘形圖。它定義了一個位置機率分佈

如果我們對這個分佈進行歸一化,使  那麼
那麼  並且
並且

我們也有

 的傅立葉變換是
的傅立葉變換是 
- 它定義了動量機率分佈

- 和

因此,與 相關的粒子的位置和動量的模糊度是"不確定性"關係所允許的最小值:
相關的粒子的位置和動量的模糊度是"不確定性"關係所允許的最小值:
現在回想一下

其中 它的傅立葉變換是
它的傅立葉變換是
![{\displaystyle \psi (t,x)={\sqrt {\sigma \over {\sqrt {\pi }}}}{1 \over {\sqrt {\sigma ^{2}+i\,(\hbar /m)\,t}}}\,e^{-x^{2}/2[\sigma ^{2}+i\,(\hbar /m)\,t]},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/110eec0173fbe62d9275715b0bcfc8cfcc7a8d57)
這定義了位置機率分佈
![{\displaystyle |\psi (t,x)|^{2}={1 \over {\sqrt {\pi }}{\sqrt {\sigma ^{2}+(\hbar ^{2}/m^{2}\sigma ^{2})\,t^{2}}}}\,e^{-x^{2}/[\sigma ^{2}+(\hbar ^{2}/m^{2}\sigma ^{2})\,t^{2}]}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d10ad7738cf0a24ceb26ca00013f418a314f1f10)
與 比較表明
比較表明 因此,
因此,
![{\displaystyle \Delta x(t)={\sigma (t) \over {\sqrt {2}}}={\sqrt {{\sigma ^{2} \over 2}+{\hbar ^{2}t^{2} \over 2m^{2}\sigma ^{2}}}}={\sqrt {[\Delta x(0)]^{2}+{\hbar ^{2}t^{2} \over 4m^{2}[\Delta x(0)]^{2}}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/98b5229e5e6f530bf65df799679a76072ca2bd81)
以下圖表說明了與 分子或花生質量的物體相比,電子質量的粒子模糊度增長得有多快。這裡我們看到了一個原因,雖然絕不是唯一的,即為什麼就所有意圖和目的而言,“一旦清晰,就永遠清晰”對宏觀物體的定位是正確的。
分子或花生質量的物體相比,電子質量的粒子模糊度增長得有多快。這裡我們看到了一個原因,雖然絕不是唯一的,即為什麼就所有意圖和目的而言,“一旦清晰,就永遠清晰”對宏觀物體的定位是正確的。
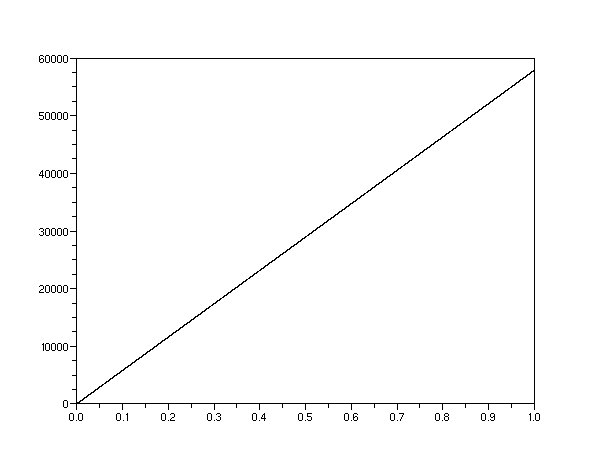
上圖:一個電子,其  奈米。一秒鐘後,
奈米。一秒鐘後, 增長到近 60 公里。
增長到近 60 公里。
下圖:一個電子,其  釐米。
釐米。  在一秒鐘內僅增長了 16%。
在一秒鐘內僅增長了 16%。

接下來,一個  分子,其
分子,其  奈米。一秒鐘後,
奈米。一秒鐘後, 增長到 4.4 釐米。
增長到 4.4 釐米。

最後,一個花生(2.8 克),其  奈米。
奈米。  需要宇宙目前的年齡才能增長到 7.5 微米。
需要宇宙目前的年齡才能增長到 7.5 微米。















![{\displaystyle \psi (t,x)={\sqrt {\sigma \over {\sqrt {\pi }}}}{1 \over {\sqrt {\sigma ^{2}+i\,(\hbar /m)\,t}}}\,e^{-x^{2}/2[\sigma ^{2}+i\,(\hbar /m)\,t]},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/110eec0173fbe62d9275715b0bcfc8cfcc7a8d57)
![{\displaystyle |\psi (t,x)|^{2}={1 \over {\sqrt {\pi }}{\sqrt {\sigma ^{2}+(\hbar ^{2}/m^{2}\sigma ^{2})\,t^{2}}}}\,e^{-x^{2}/[\sigma ^{2}+(\hbar ^{2}/m^{2}\sigma ^{2})\,t^{2}]}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d10ad7738cf0a24ceb26ca00013f418a314f1f10)


![{\displaystyle \Delta x(t)={\sigma (t) \over {\sqrt {2}}}={\sqrt {{\sigma ^{2} \over 2}+{\hbar ^{2}t^{2} \over 2m^{2}\sigma ^{2}}}}={\sqrt {[\Delta x(0)]^{2}+{\hbar ^{2}t^{2} \over 4m^{2}[\Delta x(0)]^{2}}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/98b5229e5e6f530bf65df799679a76072ca2bd81)






