三角函式/餘弦加法公式

餘弦公式

我們證明了正弦加法公式；現在我們將證明餘弦加法公式。

$\cos(\alpha +\beta )=\cos(\alpha )\cos(\beta )-\sin(\alpha )\sin(\beta )$

在進行證明之前，我們將討論減法公式。

減法公式 您無需學習或記憶正弦和餘弦的特殊減法公式或“角差”公式。您可以使用正弦和餘弦加法公式“立即”計算出它們，使用 $\sin(-x)=-\sin(x)$ 和 $\cos(-x)=\cos(x)$ 。 讓我們將 $\displaystyle (-\beta )$ 代替 $\displaystyle \beta$ 代入兩個加法公式 首先是正弦加法公式 $\sin(\alpha +\beta )=\sin(\alpha )\cos(\beta )+\cos(\alpha )\sin(\beta )$ 變為 $\sin {\big (}\alpha +(-\beta ){\big )}=\sin(\alpha )\cos(-\beta )+\cos(\alpha )\sin(-\beta )$ $\sin(\alpha -\beta )=\sin(\alpha )\cos(\beta )-\cos(\alpha )\sin(\beta )$ 現在是餘弦加法公式 $\cos(\alpha +\beta )=\cos(\alpha )\cos(\beta )-\sin(\alpha )\sin(\beta )$ 變為 $\cos {\big (}\alpha +(-\beta ){\big )}=\cos(\alpha )\cos(-\beta )-\sin(\alpha )\sin(-\beta )$ $\cos(\alpha -\beta )=\cos(\alpha )\cos(\beta )+\sin(\alpha )\sin(\beta )$ 將四個公式結合起來 如果我們真的想的話，可以將四個加法和“角差”公式用更簡潔的記號寫成 $\cos(\alpha \pm \beta )=\cos(\alpha )\cos(\beta )\mp \sin(\alpha )\sin(\beta )$ $\sin(\alpha \pm \beta )=\sin(\alpha )\cos(\beta )\pm \cos(\alpha )\sin(\beta )$ 如果你喜歡這種風格，就用它吧。我們建議你還是先學習加法公式，當你需要差值公式時，再從加法公式推匯出來。

現在要證明

$\cos(\alpha +\beta )=\cos(\alpha )\cos(\beta )-\sin(\alpha )\sin(\beta )$

如約所說。

證明

影片連結

有很多關於證明的影片

• 證明：$\cos(a+b)=\cos(a)\cos(b)-\sin(a)\sin(b)$

證明過程

我們需要證明

$\cos(\alpha +\beta )=\cos(\alpha )\cos(\beta )-\sin(\alpha )\sin(\beta )$

我們將使用上一頁練習中使用的技巧，設定 $AB=1$，並使用與上次完全相同的圖形。

由於$\triangle ABE$ 是一個直角三角形，斜邊長度為 1，角 $\beta$，因此我們有

${\overline {BE}}=\sin(\beta )$

${\overline {AE}}=\cos(\beta )$

同樣，因為$\triangle ABC$ 是一個直角三角形，斜邊長度為 1，角 $(\alpha +\beta )$，因此我們有

${\overline {AC}}=\cos(\alpha +\beta )$

讓我們用角度的餘弦和正弦來表示${\overline {AF}}$ 和 ${\overline {DE}}$。你需要檢視圖表以瞭解我們正在使用哪些三角形。

對於${\overline {AF}}$ 的表示式 ${\overline {AF}}={\overline {AE}}\cos(\alpha )$ 所以 ${\overline {AF}}=\cos(\alpha )\cos(\beta )$

對於${\overline {DE}}$ 的表示式 ${\overline {DE}}={\overline {BE}}\sin(\alpha )$ 所以 ${\overline {DE}}=\sin(\alpha )\sin(\beta )$

$\cos(\alpha +\beta )={\overline {AC}}={\overline {AF}}-{\overline {CF}}={\overline {AF}}-{\overline {DE}}$

$\cos(\alpha +\beta )=\cos(\beta )\cos(\alpha )-\sin(\beta )\sin(\alpha )=\cos(\alpha )\cos(\beta )-\sin(\alpha )\sin(\beta )$

完成！

另一種方法

這個證明看起來非常類似於 $\sin(\alpha +\beta )$

例項：從正弦加法公式推匯出餘弦加法公式

從

$\sin(\alpha +\beta )=\sin(\alpha )\cos(\beta )+\cos(\alpha )\sin(\beta )$

我們使用 $\sin(x)=\cos(90^{\circ }-x)$ 和 $\cos(x)=\sin(90^{\circ }-x)$ （並在多個地方進行替換）

$\cos {\big (}90^{\circ }-(\alpha +\beta ){\big )}=\cos(90^{\circ }-\alpha )\cos(\beta )+\sin(90^{\circ }-\alpha )\sin(\beta )$

現在我們使用 $\cos(-x)=\cos(x)$ 和 $\sin(-x)=-\sin(x)$

$\cos {\big (}-(90^{\circ }-(\alpha +\beta )){\big )}=\cos {\big (}-(90^{\circ }-\alpha ){\big )}\cos(\beta )-\sin {\big (}-(90^{\circ }-\alpha ){\big )}\sin(\beta )$

$\cos(\alpha +\beta -90^{\circ })=\cos(\alpha -90^{\circ })\cos(\beta )-\sin(\alpha -90)\sin(\beta )$

這對所有$\alpha ,\beta$都成立，所以如果我們令$\alpha =A+90^{\circ }$和$\beta =B$，我們得到

$\cos(A+B)=\cos(A)\cos(B)-\sin(A)\sin(B)$

現在輪到您練習從舊公式中推匯出新公式了

練習：從餘弦加法公式推匯出正弦加法公式 從 $\cos(\alpha +\beta )=\cos(\alpha )\cos(\beta )-\sin(\alpha )\sin(\beta )$ 證明 $\sin(\alpha +\beta )=\sin(\alpha )\cos(\beta )+\cos(\alpha )\sin(\beta )$

一個更難的練習

練習：正切加法公式 使用 $\tan(x)={\frac {\sin(x)}{\cos(x)}}$ 以及正弦和餘弦的加法公式，證明 $\tan(A+B)={\frac {\tan(A)+\tan(B)}{1-\tan(A)\tan(B)}}$

現在輪到您進行加法公式的幾何證明了。

練習：使用不同的圖表進行證明 您可能想跳過此練習，並在使用餘弦加法公式一段時間後再來做。這是讓您自信地自己編寫公式的幾何證明的一個很好的練習。 從下圖開始 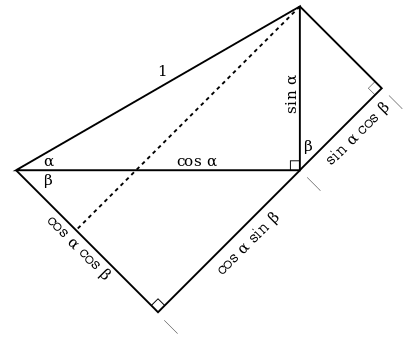新增標籤，並寫出證明 正弦加法公式 餘弦加法公式 基於圖表和您選擇的字母。確保您透過追溯角度來解釋為什麼標有$\beta$的兩個角度是相同的。給邊緣長度的標籤是為了幫助您。您的證明必須使用三角關係來解釋為什麼這些標籤是正確的。 比較上面的證明中的圖表。它們真的有多不同？