三角學/正弦平方圖

正弦平方

下圖顯示了$(\sin(x))^{2}$ 或 $\sin ^{2}(x)$ 的圖形，如通常所寫。

這個函式

• 必須是非負的，因為負數的平方總是正的。
• 不能超過 1，因為 $\sin(x)$ 始終介於 -1 和 1 之間。

它看起來像一個平移壓縮過的正弦或餘弦波。它確實是。當我們檢視二倍角公式並證明 $\sin ^{2}(x)={\frac {1-\cos(2x)}{2}}$ 時，我們將證明這一點。

練習：點檢 圖形正確嗎？嘗試一些實際值，看看它們是否被繪製在正確的位置。 在該圖形中，任何$\sin(x)=0$ 的值也將為零。 在該圖形中，任何$\sin(x)=\pm 1$ 的值將為 1。 在該圖形上具有$y=0.5$ 的值呢？哪些$\sin(x)$ 值有效？

幅度、頻率和相位 從$\sin(x)$ 到$\sin ^{2}(x)$ 幅度減半。（y 值介於 0 和 +1 之間，之前介於 -1 和 +1 之間）。 頻率加倍。（在相同的 x 距離內有更多完整的迴圈）。 相位...好吧，我們可以說相位發生了變化，但只有比較兩個相同頻率的波的相位才有意義，因此很難說相位發生了什麼變化。

餘弦平方

下圖對 $\cos ^{2}(x)$ 進行了同樣的操作。

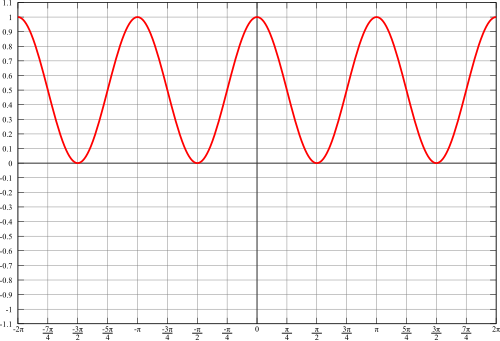
同樣，這個函式

• 必須是非負的，因為負數的平方總是正的。
• 不能超過 1，因為 $\cos(x)$ 始終介於 -1 和 1 之間。

比較這兩個圖形，它們看起來會加起來為 1。它們確實如此。這是一種圖形方式來展示我們之前已經看到的內容，即

$\cos ^{2}(x)+\sin ^{2}(x)=1$

餘弦平方公式 利用我們已經證明的結論 $\cos ^{2}(x)+\sin ^{2}(x)=1$ 並假設稍後我們將證明的結果 $\sin ^{2}(x)={\frac {1-\cos(2x)}{2}}$ 求解表示式 $\cos ^{2}(x)=$ 注意符號和括號，因為你正在對一個負數取負數。確保簡化公式 - 你的答案應該至少與$\sin ^{2}(x)$公式一樣簡單。 你得出的公式看起來與我們為$\cos ^{2}(x)$繪製的圖形一致嗎？