三角學/入門

三角學是研究三角形性質的學科。

• "Tri" 是古希臘語中的三個，
• "gon" 意思是角，
• "metry" 測量

合起來就是 "測量三角形的三個角"。

如果你知道一個三角形的一些資訊，例如它的邊長，那麼使用三角學，你就可以找到關於它的其他資訊。如果你知道邊長，那麼你可以找到角度。如果你知道一邊的長度和兩個角，那麼你就可以計算出剩下的角，以及另外兩邊的長度。

因此，古希臘人能夠利用三角學來計算地球到月球的距離。

開始學習三角學

直角三角形

我們學習三角學的第一件事就是如何在給定另外兩個角的情況下計算三角形的第三個角。例如，在一個三角形中，如果兩個角是 $60^{\circ }\,$，那麼第三個角也必須是 $60^{\circ }\,$，因為我們知道它們必須加起來等於 $180^{\circ }\,$。

但是，如果我們被告知兩個邊長，比如 7cm 和 10cm，並且沒有被告知任何關於角的資訊，那麼第三個邊長就有一系列的可能性，它可以在 0 到 17cm 之間。

在直角三角形中求解

記住，一個直角三角形有一個角是 $90^{\circ }\,$（一個 "直角"）。計算直角三角形上缺失的第三個角要簡單得多，所以我們將從考察一個直角三角形開始，預計在本書的其餘部分會看到更多這樣的三角形。

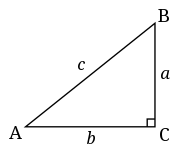
在直角三角形中，如果給出兩個較短邊的長度，我們可以計算出最長邊的長度。在直角三角形中，邊長之間有特別好的關係。這種關係的公式寫成

$a^{2}+b^{2}=c^{2}\!\,$

邊 $a$ 和 $b$ 是與 $90^{\circ }\,$ 角相鄰的邊，而 $c$ 是與之相對的較長的對角線。你可能有時會看到 $c$ 被稱為斜邊。

參見 勾股定理，開始使用此公式來計算缺失邊長的長度。

在其他形狀中求解

但是，如果三角形不是直角三角形呢？

更復雜的三角形可以很容易地分成直角三角形，因此我們學習直角三角形使我們能夠處理其他型別的三角形。三角學和三角函式也可以用於更復雜的形狀，例如正方形、六邊形、圓形和橢圓形。最終，我們用來測量宇宙的最重要的數學工具是基於對三角形數學的研究。

三角學是你的數學教育中的一個基本步驟。從看似簡單的形狀，直角三角形，我們獲得了工具和見解，幫助我們進行實際和理論上的努力。直角三角形、圓形、正弦波和指數曲線之間的微妙數學關係，只有在建立了堅實的三角學基礎之後才能完全理解。

應用

三角形用於建築。這是屋頂的一部分。

由於許多物理問題可以用三角形來表達，因此三角學在物理科學和工程領域得到了廣泛的應用。

三角學是測量和建築所必需的，因為三角形中的長度和角度之間的關係直接使用。

土木工程師、機械工程師和物理學家使用三角學來理解力如何施加以及不同的物體在互相推或碰撞時將朝哪個方向運動。

三相交流波形。三角函式在電氣工程中使用

由於三角函式對映到圓，而圓對映到波（我們將解釋這一切是如何工作的！），電氣工程師使用三角學來進行有關他們所處理的波形模式的計算，例如從牆壁上出來的交流電或手機的無線電訊號。

電影和電子遊戲中出現的計算機圖形實際上是在你的螢幕上渲染了數百萬個小三角形，儘管之後還有一些小技巧讓畫面看起來更加流暢和圓滑。