三角學/證明：勾股定理

在直角三角形中
斜邊的平方
等於
另外兩邊的平方之和。

通常稱為：$c^{2}=a^{2}+b^{2}$ （其中 $c$ 是斜邊）或 ${\text{hyp}}^{2}={\text{leg}}^{2}+{\text{leg}}^{2}$

這個定理可能比任何其他定理都有更多已知的證明；這本書《勾股定理》包含 370 種證明。^[1]

減法證明

使用四個相同直角三角形面積減法的證明

此證明使用重新排列。該圖顯示了兩個相同的邊長為 $a+b$ 的大方形。

• 頂部方形包含斜邊上的方形加上四個相同直角三角形，位於它的四個角。
• 在底部，相同的方形包含另外兩邊上的方形加上相同的四個直角三角形，現在移動到形成兩個長方形，邊長為 $a,b$ ，位於底部兩個角。

從兩個相同的方形中，邊長為 $a,b,c$ 的相同的四個直角三角形的面積被減去（彩色）。減去三角形會從面積相等的方形中移除相同的（彩色）面積，因此剩餘的白色區域，$c^{2}$ 和 $a^{2}+b^{2}$，是相等的。

...就是這樣！

歐幾里得的證明

歐幾里得《幾何原本》中的證明

歐幾里得的證明要複雜得多，它依賴於將圖形細分為各個部分並表明這些部分是全等的。這是一個數學史的片段。你不必記住這個證明。事實上，如果你第一次讀這本書，完全可以跳過它，直接進入“練習：拼圖三角形”。

為什麼這個證明在這裡？部分原因是為了表明證明事物的方法不止一種。部分原因是，歐幾里得非常謹慎地以小步進行，他之前已經證明了每一步。在“減法證明”中，我們使用了關於面積及其組成部分如何組合的知識，這些知識是真實的，但我們還沒有真正證明過。

概括來說，歐幾里得《幾何原本》中的證明是這樣的。方形被分成左右兩個長方形。構建一個三角形，它的面積是左長方形的一半。然後構建另一個三角形，它的面積是左邊的方形的一半。表明這兩個三角形是全等的，證明了這個方形與左長方形面積相同。這個論點之後是關於右邊長方形和剩餘方形的類似版本。將兩個長方形組合在一起以重新形成斜邊上的方形，它的面積等於另外兩個方形面積之和。細節如下。

設 $A,B,C$ 是直角三角形的三個頂點，直角位於 $A$。從 $A$ 向斜邊上的方形的相對邊畫垂線。這條線將斜邊上的方形分成兩個長方形，每個長方形的面積都與一條腿上的方形面積相同。

對於形式證明，我們需要四個基本的引理（證明完整證明的一步）

1. 如果兩個三角形有兩條邊分別相等，並且包含這兩條邊的角相等，那麼這兩個三角形是全等的（邊角邊）。
2. 三角形的面積等於以相同底邊且具有相同高的任何平行四邊形的面積的一半。
3. 長方形的面積等於兩條相鄰邊的乘積。
4. 方形的面積等於其兩條邊的乘積（來自 3）。

接下來，每個頂部的正方形都與一個三角形相等，該三角形又與構成底部正方形的兩個矩形之一相等。

包括新線條的插圖

證明如下：

1. 令$\triangle ACB$ 為一個直角三角形，直角為 $\angle CAB$ 。
2. 在每條邊 $BC,AB,CA$ 上繪製正方形，依次為 $CBDE,BAGF,ACIH$ 。繪製正方形需要歐幾里得的先前定理，並且依賴於平行公設。
3. 從 $A$ 作一條平行於 $BD$ 和 $CE$ 的直線。該直線將垂直地與 $BC$ 和 $DE$ 相交於 $K$ 和 $L$ ，分別。
4. 連線 $CF$ 和 $AD$ ，形成三角形 $\triangle BCF,\triangle BDA$ 。
5. $\angle CAB,\angle BAG$ 都是直角；因此 $C,A,G$ 共線。類似地，$B,A,H$ 共線。

證明矩形 $BDLK$ 和正方形 $BAGF$ 面積的一半的兩個全等三角形

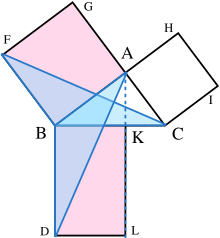
1. 角 CBD 和 FBA 都是直角；因此角 ABD 等於角 FBC，因為兩者都是直角和角 ABC 的和。
2. 由於 AB 和 BD 分別等於 FB 和 BC，因此三角形 ABD 必須與三角形 FBC 全等。
3. 由於 A 與 K 和 L 共線，因此矩形 BDLK 的面積必須是三角形 ABD 的兩倍，因為它與 BK 共高，與 BD 共底，而三角形的面積是其底和高的積的一半。
4. 由於 C 與 A 和 G 共線，因此正方形 BAGF 的面積必須是三角形 FBC 的兩倍。
5. 因此，矩形 BDLK 的面積必須等於正方形 BAGF 的面積 = AB²。
6. 類似地，可以證明矩形 CKLE 的面積必須等於正方形 ACIH 的面積 = AC²。
7. 將這兩個結果相加，得 AB² + AC² = BD × BK + KL × KC。
8. 由於 BD = KL，因此 BD* BK + KL × KC = BD(BK + KC) = BD × BC。
9. 因此 AB² + AC² = BC²，因為 CBDE 是一個正方形。

…我們完成了。

這個證明出現在歐幾里得的《幾何原本》中，作為第 1 卷第 47 題的證明，它證明了斜邊上的正方形的面積等於另外兩個正方形的面積之和。

鳴謝

• 感謝維基百科頁面 勾股定理 提供了本頁面的初始版本。更多註釋和參考資料請參見該頁面。