控制系統/框圖

在設計或分析系統時，通常使用圖形方法對系統進行建模非常有用。框圖是一種對系統進行圖形分析的有用且簡單的方法。在紙上，一個“方塊”的圖形表示恰好對應於它在系統中的實際功能

串聯絡統

當兩個或多個系統串聯時，它們可以組合成一個單一的代表系統，其傳遞函式是各個系統的傳遞函式的乘積。

如果我們有兩個系統，f(t)和g(t)，我們可以將它們串聯起來，使得系統f(t)的輸出作為系統g(t)的輸入。現在，我們可以根據使用經典方法還是現代方法對它們進行分析。

如果我們將第一個系統的輸出定義為h(t)，我們可以將h(t)定義為

$h(t)=x(t)*f(t)$

現在，我們可以用h(t)來定義系統輸出y(t)

$y(t)=h(t)*g(t)$

我們可以擴充套件h(t)

$y(t)=[x(t)*f(t)]*g(t)$

但是，由於卷積是結合的，我們可以將其重寫為

$y(t)=x(t)*[f(t)*g(t)]$

因此，我們的系統可以簡化為

串聯傳遞函式

如果兩個或多個系統串聯，則串聯的總傳遞函式是所有單個系統傳遞函式的乘積。

在時域，我們知道

$y(t)=x(t)*[f(t)*g(t)]$

但是，在頻域，我們知道卷積變成了乘法，所以我們可以將其重寫為

$Y(s)=X(s)[F(s)G(s)]$

我們可以用頻域來表示我們的系統

串聯狀態空間

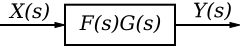
如果我們有兩個串聯的系統（例如系統 F 和系統 G），其中 F 的輸出是 G 的輸入，我們可以寫出每個單獨系統的狀態空間方程。

系統 1

$x_{F}'=A_{F}x_{F}+B_{F}u$

$y_{F}=C_{F}x_{F}+D_{F}u$

系統 2

$x_{G}'=A_{G}x_{G}+B_{G}y_{F}$

$y_{G}=C_{G}x_{G}+D_{G}y_{F}$

我們可以將這些方程式組合起來，形成具有輸入 u 和輸出 y_G 的系統 H 的完整響應。

[級聯狀態方程式]

${\begin{bmatrix}x_{G}'\\x_{F}'\end{bmatrix}}={\begin{bmatrix}A_{G}&B_{G}C_{F}\\0&A_{F}\end{bmatrix}}{\begin{bmatrix}x_{G}\\x_{F}\end{bmatrix}}+{\begin{bmatrix}B_{G}D_{F}\\B_{F}\end{bmatrix}}u$

[級聯輸出方程式]

${\begin{bmatrix}y_{G}\\y_{F}\end{bmatrix}}={\begin{bmatrix}C_{G}&D_{G}C_{F}\\0&C_{F}\end{bmatrix}}{\begin{bmatrix}x_{G}\\x_{F}\end{bmatrix}}+{\begin{bmatrix}D_{G}D_{F}\\D_{F}\end{bmatrix}}u$

並聯系統

方框不能直接並聯，需要使用加法器。如上所示，透過加法器連線的方框的總傳遞函式為

$Y(s)=X(s)[F(s)+G(s)]$

由於拉普拉斯變換是線性的，我們可以很容易地將它轉換為時域，將乘法轉換為卷積

$y(t)=x(t)*[f(t)+g(t)]$

狀態空間模型

狀態空間方程式，當 A、B、C 和 D 矩陣不為零時，概念上模擬了以下系統

在這個圖中，中間的奇怪方框要麼是一個積分器，要麼是一個理想延時，可以用傳遞域表示為

${\frac {1}{s}}$ 或 ${\frac {1}{z}}$

取決於系統的時域特性。如果我們只考慮連續時間系統，我們可以用積分器替換中間的奇怪方框。

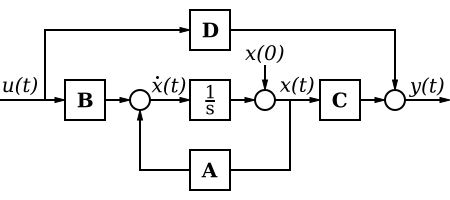
在拉普拉斯域

如果 *A*、*B*、*C* 和 *D* 是各個子系統的傳遞函式 *A(s)*、*B(s)*、*C(s)* 和 *D(s)*，並且如果 *U(s)* 和 *Y(s)* 代表單個輸入和輸出，則上述系統的狀態空間模型可以寫成如下

${\frac {Y(s)}{U(s)}}=B(s)\left({\frac {1}{s-A(s)}}\right)C(s)+D(s)$

我們將在下一章解釋如何得到這個結果，以及如何處理前饋和反饋迴路結構。

加法器和乘法器

某些系統可能包含專門的求和或乘法裝置，這些裝置會自動將多個系統的傳遞函式加在一起或相乘。

簡化方框圖

方框圖可以系統地簡化。請注意，此表來自 Schaum's Outline: Feedback and Controls Systems by DiStefano et al

變換		方程式	方框圖	等效方框圖
1	級聯方框	$Y=\left(P_{1}P_{2}\right)X$
2	串聯組合模組	$Y=P_{1}X\pm P_{2}X$
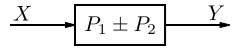
3	從前向迴路中移除模組	$Y=P_{1}X\pm P_{2}X$
4	消除反饋迴路	$Y=P_{1}\left(X\mp P_{2}Y\right)$
5	從反饋迴路中移除模組	$Y=P_{1}\left(X\mp P_{2}Y\right)$
6	重新排列求和節點	$Z=W\pm X\pm Y$
7	將求和節點移到模組前面	$Z=PX\pm Y$
8	將求和節點移到模組後面	$Z=P\left(X\pm Y\right)$
9	將取樣點移到模組前面	$Y=PX\,$
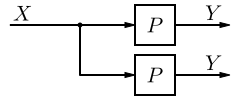
10	將取樣點移到模組後面	$Y=PX\,$
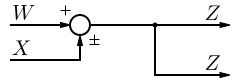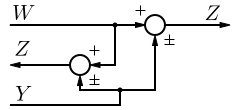
11	將取樣點移到求和節點前面	$Z=W\pm X$
12	將取樣點移到求和節點後面	$Z=X\pm Y$

外部連結

• ControlTheoryPro.com上的單輸入單輸出（SISO）框圖，包含傳遞函式

← 增益

控制系統

反饋迴路 →