控制系統/反饋迴路

華夏公益教科書的

控制系統

與控制工程

所有版本

反饋

反饋迴路是設計控制系統時一種常見且強大的工具。反饋迴路考慮了系統輸出，使系統能夠調整其效能以滿足所需的輸出響應。

在談論控制系統時，重要的是要記住，工程師通常會得到現有的系統，例如執行器、感測器、電機和其他具有設定引數的裝置，並被要求調整這些系統的效能。在許多情況下，可能無法開啟系統（“物件”）並從內部進行調整：需要對系統外部進行修改，以迫使系統響應按預期方式運作。這是透過在系統中新增控制器、補償器和反饋結構來實現的。

基本反饋結構

維基百科在反饋中有相關資訊。

這是一個基本的反饋結構。在這裡，我們使用系統的輸出值來幫助我們準備下一個輸出值。這樣，我們就可以建立能夠糾正錯誤的系統。在這裡，我們看到一個值為一的反饋迴路。我們稱之為單位反饋。

以下是一些將在以下部分中使用的相關詞彙列表

物件: 術語“物件”是從化學工程中借用的，指的是主要的系統過程。物件是預先存在的系統，如果沒有控制器的幫助，它將無法滿足給定的規格。物件通常是“現有的”，並且不可更改。在上圖中，物件用 P 表示。
控制器: 控制器或“補償器”是新增到物件中的一個附加系統，以控制物件的執行。系統可以有多個補償器，它們可以出現在系統的任何地方：在取樣節點之前，在求和器之後，在物件之前或之後，以及在反饋迴路中。在上圖中，我們的補償器用 C 表示。

一些文字或其他學科的文字可能將“求和器”稱為加法器。

求和器: 求和器是系統圖上的一個符號（在上圖中用括號表示），它在概念上將兩個或多個輸入訊號相加，併產生一個單一的和輸出訊號。
取樣節點: 取樣節點僅僅是線路上分支的代名詞。
前向通路: 反饋迴路中的前向通路是求和器之後，穿過物件並走向系統輸出的通路。
反向通路: 反向通路是取樣節點之後，迴圈回系統開始的通路。這也被稱為“反饋通路”。
單位反饋: 當反饋通路的乘法值為 1 時。

負反饋與正反饋

事實證明，負反饋幾乎總是最有用的反饋型別。當我們將輸出值從輸入值（我們期望的值）中減去時，我們得到一個稱為誤差訊號的值。誤差訊號顯示了我們的輸出與我們期望的輸入相差多遠。

正反饋具有訊號傾向於自我增強並變大的特性。在正反饋系統中，來自系統的噪聲被加回到輸入，這反過來又會產生更多噪聲。作為一個正反饋系統的例子，考慮一個帶有揚聲器和麥克風的音訊放大系統。將麥克風放置在揚聲器附近會建立一個正反饋迴路，結果是聲音變得越來越響亮。由於大多數電氣系統中的噪聲都是高頻的，因此係統的聲輸出會變得尖銳。

示例：狀態空間方程

在上一章中，我們向您展示了這張圖片

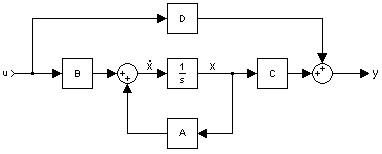
現在，我們將推匯出 I/O 關係到狀態空間方程。如果我們檢查最裡面的反饋迴路，我們可以看到前向通路有一個積分器系統， ${\frac {1}{s}}$ ，反饋迴路具有矩陣值 A。如果我們只取這個迴路的傳遞函式，我們會得到

T_{inner}(s)={\frac {\frac {1}{s}}{1-{\frac {1}{s}}A}}={\frac {1}{s-A}}

用因子 B 左乘，用 C 右乘，我們得到整個下半部分迴路的傳遞函式

T_{lower}(s)=B\left({\frac {1}{s-A}}\right)C

我們可以看到上通路（D）和下通路 T_lower 相加在一起產生最終結果

T_{total}(s)=B\left({\frac {1}{s-A}}\right)C+D

現在，對於另一種方法，我們可以假設x' 是最裡面的反饋迴路的值，位於積分器之前。這是有道理的，因為x' 的積分應該是x（從圖中我們可以看到它確實是這樣的。用u 作為輸入，解出x'，我們得到

x'=Ax+Bu

這是因為來自反饋分支的值等於值 **x** 乘以反饋迴路矩陣 A，而來自求和器左側的值等於輸入 **u** 乘以矩陣 B。

如果我們用 **x** 和 **u** 來表示，我們可以看到系統輸出是 **u** 乘以前饋值 D 和 **x** 的值乘以值 C 的總和。

y=Cx+Du

最後兩個方程正是我們系統的狀態空間方程。

反饋迴路傳遞函式

我們可以透過一系列方程來求解系統的輸出。

E(s)=X(s)-Y(s)

Y(s)=G(s)E(s)

當我們解出 Y(s) 時，得到

[反饋傳遞函式]

Y(s)=X(s){\frac {Gp(s)}{1+Gp(s)}}

鼓勵讀者自己使用上述方程推匯出結果。

函式 E(s) 被稱為 **誤差訊號**。誤差訊號是系統輸出 (Y(s)) 和系統輸入 (X(s)) 之間的差。請注意，誤差訊號現在是系統 G(s) 的直接輸入。X(s) 現在被稱為 **參考輸入**。負反饋迴路的目的是透過識別 X(s) 和 Y(s) 之間的較大差異並對其進行校正，使系統輸出等於系統輸入。

示例：電梯

這是一個關於參考輸入和反饋系統的簡單示例。

某棟樓裡有一部電梯，有 5 層樓。按下按鈕“1”會把你送到一樓，按下按鈕“5”會把你送到五樓，等等。為了簡單起見，一次只能按一個按鈕。

按下特定的按鈕是系統的參考輸入。按下“1”會給系統一個參考輸入 1，按下“2”會給系統一個參考輸入 2，等等。然後，電梯系統試圖使輸出（電梯的物理樓層位置）與參考輸入（在電梯中按下的按鈕）匹配。誤差訊號 e(t) 表示參考輸入 x(t) 和時間 t 時電梯的物理位置 y(t) 之間的差異。

假設電梯在一樓，並且在時間 t₀ 時按下了按鈕“5”。然後參考輸入成為一個階躍函式。

x(t)=5u(t-t_{0})

我們在“樓層”單位中測量。在時間 t₀ 時，誤差訊號為

e(t_{0})=x(t_{0})-y(t_{0})=5-1=4

這意味著電梯需要向上行駛 4 層。在時間 t₁ 時，當電梯在二樓時，誤差訊號為

e(t_{1})=x(t_{1})-y(t_{1})=5-2=3

這意味著電梯還有 3 層要走。最後，在時間 t₄ 時，當電梯到達頂層時，誤差訊號為

e(t_{4})=x(t_{4})-y(t_{4})=5-5=0

當誤差訊號為零時，電梯停止移動。本質上，我們可以定義三種情況。

e(t) 為正數：在這種情況下，電梯向上移動一層，然後再次檢查。
e(t) 為零：電梯停止。
e(t) 為負數：電梯向下移動一層，然後再次檢查。

狀態空間反饋迴路

在狀態空間表示中，工廠通常由狀態空間方程定義。

x'(t)=Ax(t)+Bu(t)

y(t)=Cx(t)+Du(t)

該系統被認為是預先存在的，矩陣 A、B、C 和 D 被認為是系統內部的（因此不可更改）。此外，在典型的系統中，狀態變數要麼是虛構的（表示為虛擬變數），要麼是不可測量的。出於這些原因，我們需要向系統新增外部元件，例如增益元件或反饋元件，以提高效能。

考慮在系統輸入端新增增益矩陣 K，以及一個負反饋元件 F，該元件乘以系統輸出 y 並新增到系統的輸入訊號中。有兩種情況

反饋元件 F 在乘以增益矩陣 K 之前從輸入中減去。
反饋元件 F 在乘以增益矩陣 K 之後從輸入中減去。

在情況 1 中，反饋元件 F 在將增益乘以輸入之前新增到輸入中。如果 v 是整個系統的輸入，那麼我們可以定義 u 為

u(t)=Fv(t)-FKy(t)

在情況 2 中，反饋元件 F 在將增益乘以輸入之後從輸入中減去。如果 v 是整個系統的輸入，那麼我們可以定義 u 為

u(t)=Kv(t)-Fy(t)

開環與閉環

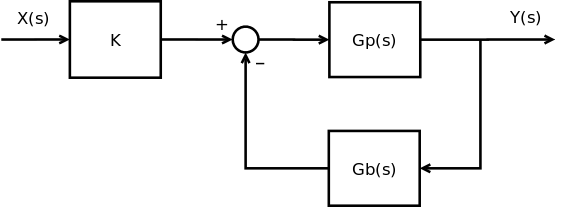
假設我們有上面所示的廣義系統。頂部部分，Gp(s) 表示所有正向路徑上的系統和控制器。底部部分，Gb(s) 表示系統中所有反饋處理元件。系統開頭的字母“K”稱為**增益**。我們將在後面的章節中更多地討論增益。我們可以定義**閉環傳遞函式**如下

[閉環傳遞函式]

H_{cl}(s)={\frac {KGp(s)}{1+Gp(s)Gb(s)}}

如果我們“開啟”迴圈，並斷開反饋節點，我們可以定義**開環傳遞函式**，如下所示

[開環傳遞函式]

H_{ol}(s)=KGp(s)

我們可以根據這個開環傳遞函式重新定義閉環傳遞函式

H_{cl}(s)={\frac {H_{ol}(s)}{1+Gp(s)Gb(s)}}

這些結果很重要，它們將在本書的其餘部分中使用，無需進一步解釋或推導。

控制器的放置

我們可以將附加控制器放置在許多不同的位置。


在系統前面，在反饋迴路之前。在反饋迴路內，在正向路徑上，在系統之前。在正向路徑上，在系統之後。在反饋迴路內，在反向路徑上。在反饋迴路之後。