控制系統/波德圖

波德圖

波德圖是一個有用的工具，它顯示了給定線性時不變 (LTI) 系統在不同頻率下的增益和相位響應。波德圖通常與給定系統的傅立葉變換一起使用。

波德幅值和相點陣圖集的一個示例。幅值圖通常位於頂部，相點陣圖通常位於圖集的底部。

波德圖的頻率繪製在對數頻率軸上。頻率軸上的每個刻度標記表示前一個值的 10 倍冪。例如，在標準波德圖上，標記的值從 (0.1, 1, 10, 100, 1000, ...) 開始。因為每個刻度標記都是 10 的冪，所以它們被稱為一個**十年**。請注意，隨著您向右移動圖表，十年的“長度”會減小。（注意，此描述與上圖不符……每個十年有 10 個刻度標記，而不是一個，但由於它是對數圖表，因此它們不是等間距的）。

波德幅值圖用稱為**分貝**的特殊單位測量系統的輸入/輸出比率。波德相點陣圖測量相移，單位為度（通常，但也使用弧度）。

分貝

**分貝**是兩個數字在對數刻度上的比率。要將兩個數字（A 和 B）之間的比率表示為分貝，我們對錶示幅值的數字應用以下公式（表示功率測量的數字使用因子 10 而不是 20）

$dB=20\log \left({A \over B}\right)$

其中 dB 是分貝結果。

或者，如果我們只想獲取單個數字 C 的分貝值，我們可以很容易地寫成

$dB=20\log(C)$

頻率響應表示法

如果我們有一個系統傳遞函式 T(s)，我們可以將其分離成一個分子多項式 N(s) 和一個分母多項式 D(s)。我們可以這樣寫

$T(s)={\frac {N(s)}{D(s)}}$

為了獲得幅值增益圖，我們必須首先使用變數更改將傳遞函式轉換為頻率響應

$s=j\omega$

從這裡，我們可以說我們的頻率響應由兩個部分組成，一個實部 R 和一個虛部 X

$T(j\omega )=R(\omega )+jX(\omega )$

我們將在下面使用這些形式。

直線逼近

波德幅值和相點陣圖可以透過使用一系列直線快速輕鬆地近似。可以透過遵循一些簡短、簡單的規則（如下所列）來生成這些近似圖。確定直線圖後，實際的波德圖是一條平滑的曲線，它遵循直線，並穿過**轉折點**。

轉折點

如果頻率響應採用零極點形式

$T(j\omega )={\frac {\prod _{n}|j\omega +z_{n}|}{\prod _{m}|j\omega +p_{m}|}}$

我們說所有 z_n 和 p_m 的值稱為波德圖的**轉折點**。這些是波德圖方向發生最大變化的值。

轉折點有時也稱為“轉折頻率”、“截止點”或“拐點”。

波德增益圖

**波德增益圖**或**波德幅值圖**顯示每個輸入頻率下系統增益的比率。

波德增益計算

傳遞函式 T 的幅值定義為

$|T(j\omega )|={\sqrt {R^{2}+X^{2}}}$

然而，將“分子/分母”形式的函式轉換為“實部+虛部”形式通常很困難。幸運的是，我們的分貝計算派上了用場。假設我們有一個頻率響應，它被定義為一個分數，其分子和分母多項式定義為

$T(j\omega )={\frac {\prod _{n}|j\omega +z_{n}|}{\prod _{m}|j\omega +p_{m}|}}$

如果我們將兩邊都轉換為分貝，則分貝計算中的對數會將引數的乘法轉換為加法，並將除法轉換為減法。

$Gain=\sum _{n}20\log(|j\omega +z_{n}|)-\sum _{m}20\log(|j\omega +p_{m}|)$

並且計算每一項的增益並將它們加在一起將給出系統在該頻率下的增益。

博德增益近似

博德幅頻圖上直線的斜率以dB/十倍頻程為單位測量，因為縱軸的單位是dB，橫軸的單位是十倍頻程。

ω = 0位於博德圖的無限左側（因為對數刻度永遠不會達到零），因此在ω = 0處找到增益的值實際上將該值設定為從圖的最左側到第一個斷點處的博德圖的增益。ω = 0處直線的斜率值為0 dB/十倍頻程。

從每個極點斷點開始，直線的斜率下降20 dB/十倍頻程。直線一直延伸到下一個斷點。從每個零點斷點開始，直線的斜率增加20 dB/十倍頻程。重複極點和零點的雙倍、三倍或更高倍數會使增益乘以相應的倍數。以下是一些示例

• 2個極點：-40 dB/十倍頻程
• 10個極點：-200 dB/十倍頻程
• 5個零點：+100 dB/十倍頻程

博德相頻圖

博德相頻圖是系統輸入頻率特性相關的輸入波形的相移圖。同樣，拉普拉斯變換不考慮系統的相移特性，但傅立葉變換可以。以“實部+虛部”形式表示的複函式的相位給出為

$\angle T(j\omega )=\tan ^{-1}\left({\frac {X}{R}}\right)$

博德圖繪製過程

給定一個零極點形式的頻率響應

$T(j\omega )=A{\frac {\prod _{n}|j\omega +z_{n}|}{\prod _{m}|j\omega +p_{m}|}}$

其中A是一個非零常數（可以是負數或正數）。

以下是繪製博德幅頻圖近似值的步驟

博德幅頻圖

步驟1

將傳遞函式分解為零極點形式。

步驟2

從傳遞函式中找到頻率響應。

步驟3

使用對數將頻率響應分離成分貝項的和

步驟4

使用$\omega =0$找到起始幅值。

步驟5

每個極點和每個零點的位置稱為斷點。在零點斷點處，直線的斜率增加20dB/十倍頻程。在極點處，直線的斜率減少20dB/十倍頻程。

步驟6

在零點斷點處，實際圖的值與直線圖的值相差3dB。零點比直線高3dB，極點比直線低3dB。

步驟7

將實際的博德圖繪製成一條平滑曲線，使其遵循前一點的直線，並穿過斷點。

以下是繪製博德相頻圖的步驟

博德相頻圖

步驟1

如果A為正，則從0度開始繪製圖形（斜率為零）。如果A為負，則從180度（或-180度，它們是相同的）開始繪製圖形，斜率為零。

步驟2

對於每個零點，當$\omega ={\frac {z_{n}}{10}}$（斷頻之前的一個十倍頻程）時，將直線向上傾斜45度/十倍頻程。多個零點意味著斜率更陡。

步驟3

對於每個極點，當$\omega ={\frac {p_{m}}{10}}$（斷頻之前的一個十倍頻程）時，將直線向下傾斜45度/十倍頻程。多個極點意味著斜率更陡。

步驟4

當相位變化了90度（對於零點）或-90度（對於極點）（或更大的值，對於多個極點或多個零點）時，再次使斜率變平。

示例

示例：恆定增益

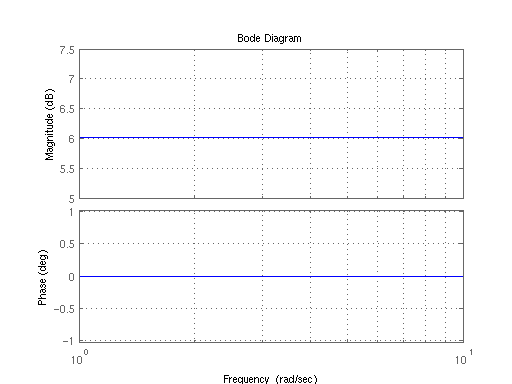
繪製一個放大器系統的博德圖，該系統具有6dB的恆定增益增加。

因為增益值是恆定的，並且不依賴於頻率，所以我們知道幅值圖在圖上的所有位置都是恆定的。沒有斷點，因此圖的斜率永遠不會改變。我們可以將圖形繪製成一條位於6dB處的水平直線。

示例：積分器

繪製由以下傳遞函式給出的完美積分器系統的博德圖：

$T(s)={\frac {2}{s}}$

首先，我們透過變數替換找到系統的頻率響應：

$T(j\omega )={\frac {2}{j\omega }}$

然後我們將幅值轉換為對數：

$Gain=20\log(2)-20\log(|j\omega |)$

注意，極點的斷點位置位於 ω → 0，也就是圖的最左邊。此外，我們注意到將 0 代入 ω 會得到一個未定義的值（當極限趨近於負無窮大時）。我們知道，由於在零點有一個單極點，因此零點右邊的圖形（也就是所有地方）的斜率為 -20dB/十倍頻程。透過將 ω → 1 代入幅值計算，我們可以確定第二項消失，此時幅值為 6dB。現在我們有了線的斜率和它與之相交的一個點，就可以繪製圖形了。

示例：微分器

$T(j\omega )=2j\omega$

示例：一階低通濾波器（1個斷點）

$T(j\omega )={\frac {2.14}{j\omega +1}}$

進一步閱讀

• 電路理論/博德圖
• ControlTheoryPro.com 上的博德圖

← 訊號流圖

控制系統

尼科爾斯圖 →