控制系統/根軌跡

問題

考慮像收音機這樣的系統。收音機有一個“音量”旋鈕，用於控制系統的增益。高音量意味著更多功率傳遞到揚聲器，低音量意味著更少功率傳遞到揚聲器。當音量值增加時，收音機傳遞函式的極點會發生變化，它們可能變得不穩定。我們想要找出收音機是否會變得不穩定，如果是，我們想要找出哪些音量值會導致它變得不穩定。我們目前的方法需要我們為每個新的音量值（增益，“K”）代入，並求解開環傳遞函式的根。這個過程可能很長。幸運的是，有一種名為根軌跡的方法，它允許我們為所有增益值繪製系統所有極點的位置圖。

根軌跡

當我們改變增益時，我們注意到系統的極點和零點實際上在S 平面中移動。當我們需要為每個新的增益值重複求解高階方程時，這一事實會讓生活變得非常困難。解決這個問題的辦法是一種稱為根軌跡圖的技術。根軌跡允許您透過遵循幾個簡單的規則來繪製所有增益值的極點和零點的位置圖。正如我們所知，風扇開關也可以控制風扇的速度。

假設我們有一個特定系統的閉環傳遞函式

${\frac {N(s)}{D(s)}}={\frac {KG(s)}{1+KG(s)H(s)}}$

其中 N 是傳遞函式的分子多項式，D 是傳遞函式的分母多項式。現在，我們知道要找到方程的極點，我們必須將分母設為 0，並求解特徵方程。換句話說，特定方程的極點位置必須滿足以下關係

$D(s)=1+KG(s)H(s)=0$

從同一個方程中，我們可以這樣操作方程

$1+KG(s)H(s)=0$

$KG(s)H(s)=-1$

最後，透過轉換為極座標

$\angle KG(s)H(s)=180^{\circ }$

現在我們有兩個方程控制著系統所有增益值的極點位置

[幅值方程]

$1+KG(s)H(s)=0$

[相位方程]

$\angle KG(s)H(s)=180^{\circ }$

數字系統

相同的基本方法可用於考慮 Z 域中的數字系統

${\frac {N(z)}{D(z)}}={\frac {KG(z)}{1+K{\overline {GH}}(z)}}$

其中 N 是關於 z 的分子多項式，D 是關於 z 的分母多項式，${\overline {GH}}(z)$ 是系統的開環傳遞函式，在 Z 域中。

根據特徵方程的定義，分母 D(z) 等於

$D(z)=1+K{\overline {GH}}(z)=0$

我們可以如下操作

$1+K{\overline {GH}}(z)=0$

$K{\overline {GH}}(z)=-1$

現在我們可以將其轉換為極座標，並取多項式的角度

$\angle K{\overline {GH}}(z)=180^{\circ }$

現在我們只剩下兩個重要的方程

[幅值方程]

$1+K{\overline {GH}}(z)=0$

[相位方程]

$\angle K{\overline {GH}}(z)=180^{\circ }$

如果您比較這兩個方程，Z 域方程與 S 域方程幾乎完全相同，作用方式也完全相同。在本章的剩餘部分，我們將只考慮 S 域方程，並且理解數字系統以幾乎相同的方式執行。

根軌跡法

注意
在本節中，S 平面和 Z 平面的規則相同，因此我們將不提及它們之間的差異。

在變換域（參見右側註釋）中，當增益較小時，極點從開環傳遞函式的極點開始。當增益變為無窮大時，極點移動到與系統的零點重疊。這意味著在根軌跡圖上，所有極點都朝零點移動。只有一個極點可以朝一個零點移動，這意味著極點的數量必須與零點的數量相同。

如果傳遞函式中的零點少於極點，則存在一定數量的隱式零點位於無窮遠處，極點將趨近於這些零點。

首先，我們需要將幅值方程轉換為稍微方便一點的形式

$KG(s)H(s)+1=0\to G(s)H(s)={\frac {-1}{K}}$

注意
我們通常用大寫字母表示頻域中的函式，但a(s)和b(s)並不重要，因此用小寫字母表示。

現在，我們可以假設 G(s)H(s) 是某種形式的分數，其分子和分母都是多項式。我們可以使用任意函式 a(s) 和 b(s) 來表示這個方程，如下所示

${\frac {a(s)}{b(s)}}={\frac {-1}{K}}$

我們將在後面的步驟中用到這些函式 a(s) 和 b(s)。

我們可以首先在圖上用“X”標記 b(s) 的根來開始繪製根軌跡。接下來，我們在圖上標記 a(s) 的根，並用“O”標記它們。

接下來，我們檢查實軸。從圖的右側開始，向左移動，我們在實軸上每經過一個實軸上奇數個極點或零點的左側，就繪製一條根軌跡線。這乍一看可能很棘手，但隨著練習會變得更容易。

現在，根軌跡線從每個極點開始。因此，在實軸上，如果兩個極點似乎透過根軌跡線相連，則這兩個極點實際上會相互靠近，然後“分離”，並離開軸線。極點離開軸線的位置稱為分離點。從這裡，根軌跡線朝最近的零點移動。

重要的是要注意，s 平面關於實軸對稱，所以在 S 平面的上半部分繪製的內容，必須在 S 平面的下半部分以映象方式繪製。

一旦極點從實軸分離，它們可以朝無窮遠移動（以遇到隱式零點），或者它們可以移動以遇到顯式零點，或者它們可以重新加入實軸以遇到位於實軸上的零點。如果極點朝無窮遠移動，它總是遵循一條漸近線。漸近線的數量等於無窮遠處的隱式零點的數量。

根軌跡法則

以下是繪製根軌跡圖的完整規則集。我們將使用 p 和 z 分別表示開環傳遞函式的極點和零點的數量。我們將使用 P_i 和 Z_i 分別表示第 i 個極點和第 i 個零點的位置。同樣，我們將使用 ψ_i 和 ρ_i 分別表示從給定點到第 i 個極點和零點的角度。所有角度都以弧度表示（π 表示 π 弧度）。

有 11 條規則，如果正確遵循，將使您能夠建立正確的根軌跡圖。

規則 1

對於 b(s) 的每個根，都有一個根軌跡分支。

規則 2

b(s) 的根是開環傳遞函式的極點。用 X 在圖上標記 b(s) 的根。

規則 3

a(s) 的根是開環傳遞函式的零點。用 O 在圖上標記 a(s) 的根。O 的數量應該小於或等於 X 的數量。在無窮遠處有 p - z 個零點。這些位於無窮遠處的零點被稱為“隱式零點”。根軌跡的所有分支將從一個極點移動到一個零點（因此，一些分支可能會朝無窮遠移動）。

規則 4

如果實軸上的一點位於奇數個極點和零點的左側，則該點是根軌跡的一部分。

規則 5

可以透過幅值方程絕對值的倒數來確定根軌跡上任何點的增益。

$\left|{\frac {b(s)}{a(s)}}\right|=|K|$

規則 6

根軌跡圖關於實軸對稱。所有復根都是共軛的。

規則 7

在實軸上相遇的兩個根將在某些分離點離開軸線。如果我們將 s → σ（沒有虛部），我們可以使用以下方程

$K=-{\frac {b(\sigma )}{a(\sigma )}}$

然後求導以找到區域性最大值

${\frac {dK}{d\sigma }}={\frac {d}{d\sigma }}{\frac {b(\sigma )}{a(\sigma )}}$

規則 8

根軌跡的分離線以 ${\frac {\pi }{\alpha }}$ 的角度分開，其中 α 是在分離點相交的極點的數量。

規則 9

根軌跡的分離線遵循漸近線，這些漸近線與實軸的交點角度為 φ_ω，其值由下式給出：

$\phi _{\omega }={\frac {\pi +2N\pi }{p-z}},\quad N=0,1,...p-z-1$

這些漸近線的起點 OA 由極點位置之和減去零點位置之和，再除以極點和零點數量之差得出。

$OA={\frac {\sum _{p}P_{i}-\sum _{z}Z_{i}}{p-z}}$

OA 點應該位於實軸上。

規則 10

根軌跡的分支在 **角度方程** 值為 π（即 180^o）的點處與虛軸相交。

規則 11

根軌跡分支與複共軛極點或零點的交角由在極點或零點附近無窮小位置分析 **角度方程** 得出。離開角 φ_d 由以下方程給出：

$\sum _{p}\psi _{i}+\sum _{z}\rho _{i}+\phi _{d}=\pi$

到達角 φ_a 由下式給出：

$\sum _{z}\rho _{i}+\sum _{p}\psi _{i}+\phi _{a}=\pi$

我們將在本章的剩餘部分解釋這些規則。

根軌跡方程

以下是兩個主要方程

[根軌跡方程]

S 域方程	Z 域方程
$1+KG(s)H(s)=0$	$1+K{\overline {GH}}(z)=0$
$\angle KG(s)H(s)=180^{o}$	$\angle K{\overline {GH}}(z)=180^{o}$

注意，所有極點和零點的角度之和必須等於 180。

漸近線數量

如果系統顯式零點的數量用 Z（大寫 z）表示，系統的極點數量用 P 表示，那麼漸近線的數量（N_a）由下式給出：

[漸近線數量]

$N_{a}=P-Z$

漸近線的角度由下式給出：

[漸近線角度]

$\phi _{k}=(2k+1){\frac {\pi }{P-Z}}$

當$k=[0,1,...N_{a}-1]$時。

漸近線交點

漸近線與實軸相交於點

[漸近線原點]

$\sigma _{0}={\frac {\sum _{P}-\sum _{Z}}{P-Z}}$

其中$\sum _{P}$是所有極點位置的總和，$\sum _{Z}$是所有顯式零點位置的總和。

分離點

分離點位於以下方程的根處

[分離點位置]

${\frac {dG(s)H(s)}{ds}}=0$ 或 ${\frac {d{\overline {GH}}(z)}{dz}}=0$

求解 z 後，實根會給出分離點/重入點。復根對應於沒有分離點/重入點。

分離點方程可能難以求解，因此很多時候實際位置是近似的。

根軌跡和穩定性

根軌跡過程應該生成一個圖，顯示系統的所有增益 K 值下的極點位置。當 D 的任何或所有根都位於不穩定區域時，系統是不穩定的。當任何根都位於臨界穩定區域時，系統是臨界穩定的（振盪的）。當 D 的所有根都位於穩定區域時，系統是穩定的。

需要注意的是，對於增益 K₁ 穩定的系統，對於不同的增益 K₂ 可能變得不穩定。一些系統可能具有在穩定和不穩定之間多次交叉的極點，從而導致多個增益值使系統不穩定。

以下是快速複習

區域	S 域		Z 域
穩定區域	左半 S 平面	$\sigma <0$	單位圓內	$|z|<1$
臨界穩定區域	縱軸	$\sigma =0$	單位圓	$|z|=1$
不穩定區域	右半 S 平面	$\sigma >0$	單位圓外	$|z|>1$

示例

示例 1：一階系統

求開環系統的根軌跡

$T(s)={\frac {1}{1+2s}}$

如果我們觀察特徵方程，我們可以快速求解系統的單個極點

$D(s)=1+2s=0$

$s=-{\frac {1}{2}}$

我們在根軌跡圖上繪製該點，並且該單個點左側實軸上的所有點都在根軌跡上（根據上述規則）。因此，我們系統的根軌跡看起來像這樣

從這張圖中，我們可以看出，對於所有增益值，該系統都是穩定的。

示例 2：三階系統

我們得到一個具有三個實極點的系統，由傳遞函式表示

$T(s)={\frac {1}{(s+1)(s+2)(s+3)}}$

這個系統穩定嗎？

為了回答這個問題，我們可以繪製根軌跡。首先，我們在圖上繪製位於 -1、-2 和 -3 的極點。第一個和第二個極點之間的實軸以及第三個極點左側的實軸都在根軌跡上。我們還知道，在某個點上會從實軸分離。漸近線的原點位於

$OA={\frac {-1+-2+-3}{3}}=-2$,

並且漸近線的角度由下式給出

$\phi ={\frac {180(2k+1)}{3}}\;\mathrm {for} \;k=0,1,2$

我們知道分離發生在第一個和第二個極點之間，因此我們將估計確切的分離點。繪製根軌跡後，我們得到以下圖形。

我們可以看到，對於較低的增益值，系統是穩定的，但是對於較高的增益值，系統變得不穩定。

示例：共軛復零點

求以下系統傳遞函式的根軌跡圖

$T(s)=K{\frac {s^{2}+4.5s+5.625}{s(s+1)(s+2)}}$

如果我們觀察分母，我們有位於原點、-1 和 -2 的極點。根據 **規則 4**，我們知道第一個和第二個極點之間的實軸以及第三個極點之後的實軸都在根軌跡上。我們還知道，在第一個和第二個極點之間會有一個分離點，這樣它們才能接近共軛復零點。如果我們對分子使用二次方程，我們可以發現零點位於

$s=(-2.25+j0.75),(-2.25-j0.75)$

如果我們繪製我們的圖形，我們將得到以下結果

我們可以從該圖中看出，對於所有 K 值，該系統都是穩定的。

示例：使用 MATLAB/Octave 繪製根軌跡

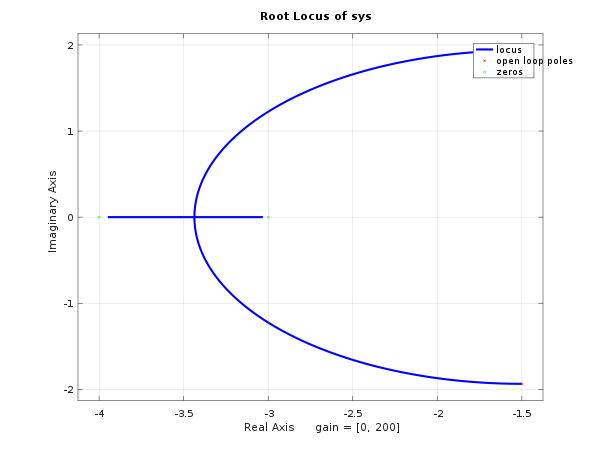
{{TextBox|1=使用 MATLAB、Octave 或其他數學模擬軟體為以下系統生成根軌跡圖

$T(s)=K{\frac {s^{2}+7s+12}{(s^{2}+3s+6)}}$

首先，我們必須將分母展開

$N(s)=S^{2}+7S+12$

$D(s)=S^{2}+3S+2$

現在，我們可以從分子和分母生成係數向量

 num = [0 1 7 12];
 den = [0 1 3 2];

接下來，我們可以將這些向量輸入到 **rlocus** 命令中

 rlocus(num, den);

**注意**: 在 Octave 中，我們需要首先透過輸入以下命令建立系統結構：

 sys = tf(num, den);
 rlocus(sys);

無論哪種方式，我們都會生成以下圖表

← Jury 檢驗

控制系統

奈奎斯特穩定性判據 →