FHSST 物理學/動量/性質

動量有哪些性質？

在這個階段，你可能想知道為什麼要引入動量。值得注意的是，動量是一個守恆量。在一個孤立的系統中，總動量是恆定的。無論發生在孤立系統內的各個物體上的任何情況，系統的總動量都不會改變！由於動量是向量，因此它的守恆意味著它的量級和方向都保持不變。

動量在孤立系統中是守恆的！

這個線性動量守恆原理是物理學中最基本的原理之一，它本身就證明了動量的定義。由於動量與物體的運動有關，我們可以利用它的守恆來預測碰撞和爆炸中會發生什麼。如果我們把兩個物體撞在一起，根據動量守恆，碰撞前兩個物體的總動量等於碰撞後的總動量。

線性動量守恆原理:

一個孤立系統的匯流排性動量是恆定的。

或者

在一個孤立系統中，碰撞前的總動量

（或爆炸）等於碰撞後的總動量

（或爆炸）。

讓我們考慮兩個檯球或撞球的簡單碰撞。考慮第一個球（質量為m₁），它具有初始速度 (${\overrightarrow {u_{1}}}$）。第二個球（質量為m₂）以初始速度 ${\overrightarrow {u_{2}}}$ 向第一個球運動。這種情況如圖 6.1 所示。如果我們將每個球的動量加起來，我們就會得到系統的總動量。然後這個總動量是

${\begin{matrix}{\overrightarrow {p}}_{total\ before}=m_{1}{\overrightarrow {u_{1}}}+m_{2}{\overrightarrow {u_{2}}},\end{matrix}}$

File:Fhsst mom2.png

圖 6.1：碰撞前。

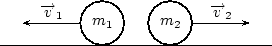
圖 6.2：碰撞後。

兩個球碰撞後分開，每個球都有不同的動量。如果我們將第一個球的最終速度稱為 ${\overrightarrow {v_{1}}}$，第二個球的最終速度稱為 ${\overrightarrow {v_{2}}}$ （見圖 6.2），那麼碰撞後系統的總動量是

${\begin{matrix}{\overrightarrow {p}}_{total\ after}=m_{1}{\overrightarrow {v_{1}}}+m_{2}{\overrightarrow {v_{2}}},\end{matrix}}$

這個由兩個球組成的系統是孤立的，因為沒有外力作用於球上。因此，根據線性動量守恆原理，碰撞前的總動量等於碰撞後的總動量。這得出了兩個物體碰撞中動量守恆的方程，

$m_{1}{\overrightarrow {u_{1}}}+m_{2}{\overrightarrow {u_{2}}}=m_{1}{\overrightarrow {v_{1}}}+m_{2}{\overrightarrow {v_{2}}}$
m1	: 物體 1 的質量（kg）
m2	: 物體 2 的質量（kg）
${\overrightarrow {u_{1}}}$	: 物體 1 的初始速度（m.s-1 + 方向）
${\overrightarrow {u_{2}}}$	: 物體 2 的初速度 (m.s-1 + 方向)
${\overrightarrow {v_{1}}}$	: 物體 1 的末速度 (m.s-1 + 方向)
${\overrightarrow {v_{2}}}$	: 物體 2 的末速度 (m.s-1 + 方向)

該等式始終成立 - 動量在碰撞中始終守恆。

章節 '碰撞和爆炸' 涉及動量守恆的應用。