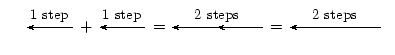FHSST 物理/向量/數學性質

向量的數學性質

向量是數學物件，我們將用它們來用數學語言描述物理。但是，首先我們需要了解向量的數學性質（例如它們如何加減）。

我們現在將使用表示位移的箭頭來說明向量的性質。請記住，位移只是向量的一個例子。我們也可以選擇使用力來說明向量的性質。

向量的加法

如果我們將位移向量定義為向前方向兩步，而另一個定義為向前方向三步，那麼將它們加在一起將意味著向前移動總共五步。從圖形上看，這可以透過首先沿著第一個向量向前兩步，然後沿著第二個向量向前三步來實現。

我們將第二個向量加在第一個向量的末端，因為這是第一個向量作用後我們現在的位置。從第一個向量的尾部（起點）到最後一個向量的頭部（終點）的向量是所有向量的總和。這就是向量加法的頭尾相連法。

向量相加的順序無關緊要。在上面的例子中，如果你先向前走三步，然後再向前走兩步，最終的結果仍然是向前走五步。

向量相加的最終答案稱為合向量。

定義：若干個向量的合向量是指單個向量，其作用與所有向量共同作用產生的效果相同。

換句話說，可以用合向量來代替各個向量——總的效果是一樣的。如果向量 ${\overrightarrow {a}}$ 和 ${\overrightarrow {b}}$ 的合向量為 ${\overrightarrow {R}}$，則可以用以下數學公式表示：${\begin{matrix}{\overrightarrow {R}}&=&{\overrightarrow {a}}+{\overrightarrow {b}}.\end{matrix}}$

讓我們再考慮一些使用位移的向量加法的例子。箭頭告訴你在哪個方向移動多遠。指向右邊的箭頭對應於向前移動，而指向左邊的箭頭對應於向後移動。檢視下面所有的例子並檢查它們。

讓我們測試第一個。它說向前一步，然後再向前一步，與一個長度是兩倍的箭頭相同——向前兩步。

你可能會回到原點。在這種情況下，你所做的事情的最終結果是你什麼地方都沒有去過（你的起點和終點在同一個位置）。在這種情況下，你的合位移是一個長度為零單位的向量。我們使用符號 ${\overrightarrow {0}}$ 來表示這樣的向量。

以同樣的方式檢查下面的例子。指向頁面的箭頭可以看作是向左移動，指向頁面下方的箭頭可以看作是向右移動。

嘗試幾個來讓自己信服！

重要的是要認識到方向並不特殊——向前和向後或向左和向右的處理方式相同。任何一組平行方向也是如此。

在上面的例子中，各個位移彼此平行。但是，相同的頭尾相連的向量加法技術可以應用於任何方向的向量。

現在你已經發現了向量的一個用途；描述合位移——經過一系列移動後你移動了多遠，哪個方向。

雖然這裡向量加法是透過位移來演示的，但所有向量都以完全相同的方式工作。因此，如果給定多個力作用於一個物體上，你可以使用相同的方法來確定作用在物體上的合力。我們將在後面詳細介紹向量加法。

向量的減法

減去一個向量是什麼意思？這很簡單：如果我們有 5 個蘋果，然後減去 3 個蘋果，就只剩下 2 個蘋果。現在讓我們用步數來進行——如果我們向前走了 5 步，然後減去向前走了 3 步，就只剩下向前走了兩步。

我們做了什麼？你最初向前走了 5 步，然後向後走了 3 步。向後的位移將由一個指向左側（向後）的箭頭表示，長度為 3。新增這兩個向量的最終結果是向前走了 2 步。

因此，從另一個向量中減去一個向量與新增一個方向相反的向量是一樣的（即減去向前走 3 步與新增向後走 3 步相同）。

這表明在這個問題中，指向右邊的箭頭是正的，而指向左邊的箭頭是負的。更一般地說，方向相反的向量符號不同（即，如果我們將向上定義為正，那麼向下作用的向量為負）。因此，改變向量的符號只是將它的方向反轉。

用數學形式表示，從 ${\overrightarrow {b}}$ 中減去 ${\overrightarrow {a}}$ 會得到一個新的向量 ${\overrightarrow {c}}$

${\begin{matrix}{\overrightarrow {c}}&=&{\overrightarrow {b}}-{\overrightarrow {a}}\\&=&{\overrightarrow {b}}+(-{\overrightarrow {a}})\end{matrix}}$

這清楚地表明，從 ${\overrightarrow {b}}$ 中減去向量 ${\overrightarrow {a}}$ 與將 $(-{\overrightarrow {a}})$ 加到 ${\overrightarrow {b}}$ 是相同的。看一下以下向量減法的示例。

標量乘法

當您將向量乘以標量（普通數字）時會發生什麼？

回到正常的乘法，我們知道 $2\times 2$ 只是 2 組 2 相加得到 4。我們可以採用類似的方法來理解向量乘法是如何工作的。