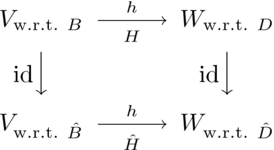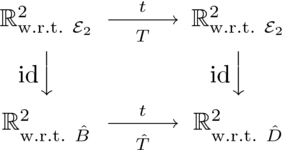線性代數/改變對映表示

線性代數
← 改變向量的表示	改變對映表示	投影 →

第一小節展示瞭如何將向量相對於一個基的表示轉換為該向量相對於另一個基的表示。在這裡我們將看到如何將對映相對於一對基的表示轉換為該對映相對於另一對基的表示。也就是說，我們想要在這個箭頭圖中矩陣之間的關係。

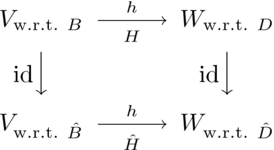
要從該圖的左下角移動到右下角，我們可以直接向右移動，或者向上移動到 $V_{B}$ ，然後向右移動到 $W_{D}$ ，然後向下移動。用矩陣表示，我們可以計算 ${\hat {H}}={\rm {Rep}}_{{\hat {B}},{\hat {D}}}(h)$ ，要麼簡單地使用 ${\hat {B}}$ 和 ${\hat {D}}$ ，要麼首先用 ${\rm {Rep}}_{{\hat {B}},B}({\mbox{id}})$ 改變基，然後乘以 $H={\rm {Rep}}_{B,D}(h)$ ，然後用 ${\rm {Rep}}_{D,{\hat {D}}}({\mbox{id}})$ 改變基。此等式總結了這一點。

{\hat {H}}={\rm {Rep}}_{D,{\hat {D}}}({\mbox{id}})\cdot H\cdot {\rm {Rep}}_{{\hat {B}},B}({\mbox{id}})\qquad \qquad (*)

(為了將這個等式與它前面的句子進行比較，請記住，這個等式是從右到左讀的，因為函式組合是從右到左讀的，而矩陣乘法代表組合。）

示例 2.1

矩陣

T={\begin{pmatrix}\cos(\pi /6)&-\sin(\pi /6)\\\sin(\pi /6)&\cos(\pi /6)\end{pmatrix}}={\begin{pmatrix}{\sqrt {3}}/2&-1/2\\1/2&{\sqrt {3}}/2\end{pmatrix}}

表示，關於 ${\mathcal {E}}_{2},{\mathcal {E}}_{2}$ ，變換 $t:\mathbb {R} ^{2}\to \mathbb {R} ^{2}$ ，它將向量 $\pi /6$ 弧度逆時針旋轉。

我們可以將該表示形式相對於 ${\mathcal {E}}_{2},{\mathcal {E}}_{2}$ 轉換為相對於

{\hat {B}}=\langle {\begin{pmatrix}1\\1\end{pmatrix}}{\begin{pmatrix}0\\2\end{pmatrix}}\rangle \qquad {\hat {D}}=\langle {\begin{pmatrix}-1\\0\end{pmatrix}}{\begin{pmatrix}2\\3\end{pmatrix}}\rangle

使用上面的箭頭圖和公式 ( $*$ )。

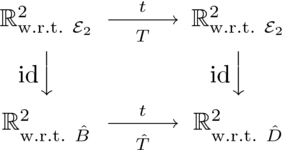
由此，我們可以使用公式

${\hat {T}}={\rm {Rep}}_{{\mathcal {E}}_{2},{\hat {D}}}({\mbox{id}})\cdot T\cdot {\rm {Rep}}_{{\hat {B}},{\mathcal {E}}_{2}}({\mbox{id}})$

注意 ${\rm {Rep}}_{{\mathcal {E}}_{2},{\hat {D}}}({\mbox{id}})$ 可以透過計算 ${\rm {Rep}}_{{\hat {D}},{\mathcal {E}}_{2}}({\mbox{id}})$ 的矩陣逆得到。

{\begin{array}{rl}{\rm {Rep}}_{{\hat {B}},{\hat {D}}}(t)&={\begin{pmatrix}-1&2\\0&3\end{pmatrix}}^{-1}{\begin{pmatrix}{\sqrt {3}}/2&-1/2\\1/2&{\sqrt {3}}/2\end{pmatrix}}{\begin{pmatrix}1&0\\1&2\end{pmatrix}}\\&={\begin{pmatrix}(5-{\sqrt {3}})/6&(3+2{\sqrt {3}})/3\\(1+{\sqrt {3}})/6&{\sqrt {3}}/3\end{pmatrix}}\end{array}}

雖然新矩陣看起來更亂，但它所代表的對映是相同的。例如，要複製 $t$ 在圖片中的效果，從 ${\hat {B}}$ 開始，

{\rm {Rep}}_{\hat {B}}({\begin{pmatrix}1\\3\end{pmatrix}})={\begin{pmatrix}1\\1\end{pmatrix}}_{\hat {B}}

應用 ${\hat {T}}$ ，

{\begin{pmatrix}(5-{\sqrt {3}})/6&(3+2{\sqrt {3}})/3\\(1+{\sqrt {3}})/6&{\sqrt {3}}/3\end{pmatrix}}_{{\hat {B}},{\hat {D}}}{\begin{pmatrix}1\\1\end{pmatrix}}_{\hat {B}}={\begin{pmatrix}(11+3{\sqrt {3}})/6\\(1+3{\sqrt {3}})/6\end{pmatrix}}_{\hat {D}}

並與 ${\hat {D}}$ 進行比較

{\frac {11+3{\sqrt {3}}}{6}}\cdot {\begin{pmatrix}-1\\0\end{pmatrix}}+{\frac {1+3{\sqrt {3}}}{6}}\cdot {\begin{pmatrix}2\\3\end{pmatrix}}={\begin{pmatrix}(-3+{\sqrt {3}})/2\\(1+3{\sqrt {3}})/2\end{pmatrix}}

以檢視它是否與上面的結果相同。

示例 2.2

在 $\mathbb {R} ^{3}$ 上，對映

{\begin{pmatrix}x\\y\\z\end{pmatrix}}{\stackrel {t}{\longmapsto }}{\begin{pmatrix}y+z\\x+z\\x+y\end{pmatrix}}

也就是說，它相對於標準基是這樣表示的

{\rm {Rep}}_{{\mathcal {E}}_{3},{\mathcal {E}}_{3}}(t)={\begin{pmatrix}0&1&1\\1&0&1\\1&1&0\end{pmatrix}}

也可以用另一個基來表示

如果 $B=\langle {\begin{pmatrix}1\\-1\\0\end{pmatrix}},{\begin{pmatrix}1\\1\\-2\end{pmatrix}},{\begin{pmatrix}1\\1\\1\end{pmatrix}}\rangle$ 那麼 ${\rm {Rep}}_{B,B}(t)={\begin{pmatrix}-1&0&0\\0&-1&0\\0&0&2\end{pmatrix}}$

以更簡單的方式，即對角矩陣的作用很容易理解。

當然，我們通常更喜歡使表示更容易理解的基變。當相對於相同起始基和結束基的表示為對角矩陣時，我們說該對映或矩陣已 **對角化**。在第五章中，我們將看到哪些對映和矩陣是可對角化的，以及在不可對角化的情況下，我們將看到如何獲得幾乎對角化的表示。

我們本節最後考慮一個更容易的情況，即表示相對於可能不同的起始基和結束基。回想一下，上一節表明矩陣改變基當且僅當它是可逆的。這給了我們上面箭頭圖和方程的另一個版本 ( $*$ ).

定義 2.3

相同大小的矩陣 $H$ 和 ${\hat {H}}$ **矩陣等價**，如果存在可逆矩陣 $P$ 和 $Q$ 使得 ${\hat {H}}=PHQ$ .

推論 2.4

矩陣等價的矩陣表示同一對映，相對於適當的基對。

問題 10 檢查矩陣等價是否是等價關係。因此它將矩陣集劃分為矩陣等價類。

所有矩陣

H

矩陣等價
到

{\hat {H}}

透過將矩陣等價與行等價進行比較，我們可以對這些類別有所瞭解（回想一下，當矩陣可以透過行運算相互簡化為彼此時，它們是行等價的）。在 ${\hat {H}}=PHQ$ 中，矩陣 $P$ 和 $Q$ 是非奇異的，因此每個都可以寫成基本約簡矩陣的乘積（見前一小節中的引理 4.8）。左乘構成 $P$ 的約簡矩陣的效果是執行行運算。右乘構成 $Q$ 的約簡矩陣執行列運算。因此，矩陣等價是行等價的推廣——如果一個矩陣可以透過一系列行約簡步驟轉換為另一個矩陣，則兩個矩陣是行等價的，而如果一個矩陣可以透過一系列行約簡步驟後跟一系列列約簡步驟轉換為另一個矩陣，則兩個矩陣是矩陣等價的。

因此，如果矩陣是行等價的，那麼它們也是矩陣等價的（因為我們可以取 $Q$ 為單位矩陣，因此不執行任何列運算）。然而，反之則不成立。

示例 2.5

這兩個

{\begin{pmatrix}1&0\\0&0\end{pmatrix}}\qquad {\begin{pmatrix}1&1\\0&0\end{pmatrix}}

是矩陣等價的，因為第二個可以透過將第一列乘以 $-1$ 並加到第二列的列運算簡化為第一個。它們不是行等價的，因為它們具有不同的簡化行梯形形式（事實上，兩者都已經是簡化形式）。

我們將透過為矩陣等價類找到一組代表來結束本節。^[1]

定理 2.6

任何 $m\!\times \!n$ 秩為 $k$ 的矩陣與 $m\!\times \!n$ 矩陣矩陣等價，該矩陣除了前 $k$ 個對角元素為 1 外，所有元素均為零。

{\begin{pmatrix}1&0&\ldots &0&0&\ldots &0\\0&1&\ldots &0&0&\ldots &0\\&\vdots \\0&0&\ldots &1&0&\ldots &0\\0&0&\ldots &0&0&\ldots &0\\&\vdots \\0&0&\ldots &0&0&\ldots &0\end{pmatrix}}

有時這被描述為塊部分單位形式。

\left({\begin{array}{c|c}I&Z\\\hline Z&Z\end{array}}\right)

證明

如上所述，對給定矩陣進行高斯-約旦消元，並將所有用於消元的矩陣組合起來，形成 $P$ 。然後利用主元進行列消元，最後交換列，將主元置於對角線上。將用於這些列操作的消元矩陣組合成 $Q$ 。

示例 2.7

我們透過尋找此矩陣的 $P$ 和 $Q$ 來說明證明過程。

{\begin{pmatrix}1&2&1&-1\\0&0&1&-1\\2&4&2&-2\end{pmatrix}}

首先進行高斯-約旦行消元。

{\begin{pmatrix}1&-1&0\\0&1&0\\0&0&1\end{pmatrix}}{\begin{pmatrix}1&0&0\\0&1&0\\-2&0&1\end{pmatrix}}{\begin{pmatrix}1&2&1&-1\\0&0&1&-1\\2&4&2&-2\end{pmatrix}}={\begin{pmatrix}1&2&0&0\\0&0&1&-1\\0&0&0&0\end{pmatrix}}

然後進行列消元，這涉及到右乘。

{\begin{pmatrix}1&2&0&0\\0&0&1&-1\\0&0&0&0\end{pmatrix}}{\begin{pmatrix}1&-2&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{pmatrix}}{\begin{pmatrix}1&0&0&0\\0&1&0&0\\0&0&1&1\\0&0&0&1\end{pmatrix}}={\begin{pmatrix}1&0&0&0\\0&0&1&0\\0&0&0&0\end{pmatrix}}

最後交換列。

{\begin{pmatrix}1&0&0&0\\0&0&1&0\\0&0&0&0\end{pmatrix}}{\begin{pmatrix}1&0&0&0\\0&0&1&0\\0&1&0&0\\0&0&0&1\end{pmatrix}}={\begin{pmatrix}1&0&0&0\\0&1&0&0\\0&0&0&0\end{pmatrix}}

最後，將左乘子合併為 $P$ ，將右乘子合併為 $Q$ ，得到 $PHQ$ 方程。

{\begin{pmatrix}1&-1&0\\0&1&0\\-2&0&1\end{pmatrix}}{\begin{pmatrix}1&2&1&-1\\0&0&1&-1\\2&4&2&-2\end{pmatrix}}{\begin{pmatrix}1&0&-2&0\\0&0&1&0\\0&1&0&1\\0&0&0&1\end{pmatrix}}={\begin{pmatrix}1&0&0&0\\0&1&0&0\\0&0&0&0\end{pmatrix}}

推論 2.8

兩個相同大小的矩陣當且僅當它們具有相同的秩時，它們是矩陣等價的。也就是說，矩陣等價類由秩來刻畫。

證明

兩個具有相同秩的相同大小的矩陣等價於同一個塊部分單位矩陣。

示例 2.9

$2\!\times \!2$ 矩陣只有三種可能的秩：零、一或二。因此，存在三個矩陣等價類。

所有 $2\!\times \!2$ 矩陣：三個等價
類

每個類包含所有具有相同秩的 $2\!\times \!2$ 矩陣。只有一個秩為零的矩陣，因此該類只有一個成員，但其他兩個類分別具有無限多個成員。

在本小節中，我們已經看到了如何將對映相對於第一對基的表示更改為相對於第二對基的表示。這導致了一個定義，描述了矩陣在這種情況下何時是等價的。最後，我們注意到，透過適當選擇（可能是不同的）起始和結束基，任何對映都可以用塊部分單位形式表示。

這種表示形式的優點之一是，在某種意義上，當對映以這種方式表達時，我們可以完全理解對映：如果基是 $B=\langle {\vec {\beta }}_{1},\dots ,{\vec {\beta }}_{n}\rangle$ 和 $D=\langle {\vec {\delta }}_{1},\dots ,{\vec {\delta }}_{m}\rangle$ ，那麼對映傳送

c_{1}{\vec {\beta }}_{1}+\dots +c_{k}{\vec {\beta }}_{k}+c_{k+1}{\vec {\beta }}_{k+1}+\dots +c_{n}{\vec {\beta }}_{n}\;\longmapsto \;c_{1}{\vec {\delta }}_{1}+\dots +c_{k}{\vec {\delta }}_{k}+{\vec {0}}+\dots +{\vec {0}}

其中 $k$ 是對映的秩。因此，我們可以將任何線性對映理解為一種投影。

{\begin{pmatrix}c_{1}\\\vdots \\c_{k}\\c_{k+1}\\\vdots \\c_{n}\end{pmatrix}}_{B}\;\mapsto \;{\begin{pmatrix}c_{1}\\\vdots \\c_{k}\\0\\\vdots \\0\end{pmatrix}}_{D}

當然，要“理解”以這種方式表達的對映，我們需要了解 $B$ 和 $D$ 之間的關係。然而，儘管有這個困難，這仍然是一個對線性對映很好的分類。 }}

練習

此練習推薦所有讀者完成。

問題 1

判斷以下矩陣是否矩陣等價。

${\begin{pmatrix}1&3&0\\2&3&0\end{pmatrix}}$ , ${\begin{pmatrix}2&2&1\\0&5&-1\end{pmatrix}}$
${\begin{pmatrix}0&3\\1&1\end{pmatrix}}$ , ${\begin{pmatrix}4&0\\0&5\end{pmatrix}}$
${\begin{pmatrix}1&3\\2&6\end{pmatrix}}$ , ${\begin{pmatrix}1&3\\2&-6\end{pmatrix}}$

此練習推薦所有讀者完成。

問題 2

求每個矩陣的矩陣等價類中的規範代表。

${\begin{pmatrix}2&1&0\\4&2&0\end{pmatrix}}$
${\begin{pmatrix}0&1&0&2\\1&1&0&4\\3&3&3&-1\end{pmatrix}}$

問題 3

假設關於

B={\mathcal {E}}_{2}\qquad D=\langle {\begin{pmatrix}1\\1\end{pmatrix}},{\begin{pmatrix}1\\-1\end{pmatrix}}\rangle

變換 $t:\mathbb {R} ^{2}\to \mathbb {R} ^{2}$ 由此矩陣表示。

{\begin{pmatrix}1&2\\3&4\end{pmatrix}}

使用基變換矩陣將 $t$ 表示為每對基。

${\hat {B}}=\langle {\begin{pmatrix}0\\1\end{pmatrix}},{\begin{pmatrix}1\\1\end{pmatrix}}\rangle$ , ${\hat {D}}=\langle {\begin{pmatrix}-1\\0\end{pmatrix}},{\begin{pmatrix}2\\1\end{pmatrix}}\rangle$
${\hat {B}}=\langle {\begin{pmatrix}1\\2\end{pmatrix}},{\begin{pmatrix}1\\0\end{pmatrix}}\rangle$ , ${\hat {D}}=\langle {\begin{pmatrix}1\\2\end{pmatrix}},{\begin{pmatrix}2\\1\end{pmatrix}}\rangle$

此練習推薦所有讀者完成。

問題 4

在方程 ${\hat {H}}=PHQ$ 中， $P$ 和 $Q$ 的大小是多少？

此練習推薦所有讀者完成。

問題 5

使用定理 2.6 來證明一個方陣是可逆的當且僅當它與單位矩陣等價。

此練習推薦所有讀者完成。

問題 6

證明當 $A$ 是一個可逆方陣時，如果 $P$ 和 $Q$ 是可逆方陣，使得 $PAQ=I$ ，則 $QP=A^{-1}$ 。

此練習推薦所有讀者完成。

問題 7

為什麼定理 2.6 不能說明每個矩陣都是可對角化的（參見例 2.2）？

問題 8

矩陣等價矩陣是否一定具有矩陣等價的轉置？

問題 9

如果 $k=0$ ，定理 2.6 會發生什麼？

此練習推薦所有讀者完成。

問題 10

證明矩陣等價是一個等價關係。

此練習推薦所有讀者完成。

問題 11

證明零矩陣在其矩陣等價類中是唯一的。還有其他類似的矩陣嗎？

問題 12

在 $\mathbb {R} ^{1}$ 和 $\mathbb {R} ^{3}$ 上的變換矩陣有哪些等價類？

問題 13

有多少個矩陣等價類？

問題 14

矩陣等價類在標量乘法和加法下是否封閉？

問題 15

設 $t:\mathbb {R} ^{n}\to \mathbb {R} ^{n}$ 由 $T$ 關於 ${\mathcal {E}}_{n},{\mathcal {E}}_{n}$ 表示。

在該特定情況下求 ${\rm {Rep}}_{B,B}(t)$ 。
$T={\begin{pmatrix}1&1\\3&-1\end{pmatrix}}\qquad B=\langle {\begin{pmatrix}1\\2\end{pmatrix}},{\begin{pmatrix}-1\\-1\end{pmatrix}}\rangle$
描述 ${\rm {Rep}}_{B,B}(t)$ 的一般情況，其中 $B=\langle {\vec {\beta }}_{1},\ldots ,{\vec {\beta }}_{n}\rangle$ 。

問題 16

設 $V$ 有基 $B_{1}$ 和 $B_{2}$ ，假設 $W$ 有基 $D$ 。設 $h:V\to W$ ，求計算 ${\rm {Rep}}_{B_{2},D}(h)$ 的公式，該公式從 ${\rm {Rep}}_{B_{1},D}(h)$ 中計算。
用一個 $V$ 的基和兩個 $W$ 的基，重複上一個問題。