我們已經將第一部分關於解集的結果翻譯成幾何術語,以便深入瞭解這些解集的外觀。但我們必須注意不要被我們自己的術語所誤導;將  的子集形式標記為
的子集形式標記為  和
和  作為“直線”和“平面”並不能使它們像我們以前經驗中的直線和平面一樣。相反,我們必須確保這些名稱適合這些集合。雖然我們無法證明這些集合滿足我們的直覺——我們無法證明關於直覺的任何東西——在本節中,我們將觀察到從
作為“直線”和“平面”並不能使它們像我們以前經驗中的直線和平面一樣。相反,我們必須確保這些名稱適合這些集合。雖然我們無法證明這些集合滿足我們的直覺——我們無法證明關於直覺的任何東西——在本節中,我們將觀察到從  和
和  熟悉的結論,當推廣到任意
熟悉的結論,當推廣到任意  時,支援直線是直的,平面是平坦的這一觀點。具體來說,我們將看到如何在它們生成的“平面”中進行歐幾里得幾何,方法是給出兩個
時,支援直線是直的,平面是平坦的這一觀點。具體來說,我們將看到如何在它們生成的“平面”中進行歐幾里得幾何,方法是給出兩個  向量之間角度的定義。
向量之間角度的定義。
- 定義 2.1
向量  的長度 為此。
的長度 為此。

我們可以使用該定義來推匯出兩個向量之間角度的公式。為了得到一個要做什麼的模型,考慮  中的兩個向量。
中的兩個向量。

將它們置於規範位置,並在它們確定的平面上,考慮由  、
、 和
和  形成的三角形。
形成的三角形。
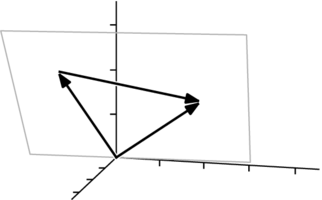
應用餘弦定理, ,其中
,其中  是向量之間的夾角。展開兩邊
是向量之間的夾角。展開兩邊


並簡化。

在更高維度中,沒有圖片足以說明,但我們可以透過分析進行同樣的論證。首先,分子形式很明顯——它來自平方  、
、 等等的中間項。
等等的中間項。
- 定義 2.3
兩個  個分量的實向量之間的 **點積**(或 **內積**,或 **標量積**)是其分量之間的線性組合。
個分量的實向量之間的 **點積**(或 **內積**,或 **標量積**)是其分量之間的線性組合。

請注意,兩個向量的點積是一個實數,而不是一個向量,並且來自  的向量與來自
的向量與來自  的向量的點積僅在
的向量的點積僅在  等於
等於  時才定義。還需要注意點積與長度之間的關係:將向量與其自身點積得到其長度的平方
時才定義。還需要注意點積與長度之間的關係:將向量與其自身點積得到其長度的平方  .
.
- 備註 2.4
該定義中的措辭允許其中一個或兩個向量都是行向量而不是列向量。一些書籍要求第一個向量是行向量,第二個向量是列向量。我們不會那麼嚴格。
仍然使用字母推理,但以圖片為指導,我們使用下一個定理來論證由  ,
, 和
和  形成的三角形位於
形成的三角形位於  中由
中由  和
和  生成的平面子集中。
生成的平面子集中。
- 定理 2.5(三角形不等式)
對於任何  ,
,

當且僅當其中一個向量是另一個向量的非負標量倍數時,等式成立。
這個不等式是“兩點之間直線最短”這一熟悉說法來源。

- 證明
(我們將使用一些尚未驗證的點積代數性質,例如 以及
以及  。參見問題 8。)所需不等式成立當且僅當其平方成立。
。參見問題 8。)所需不等式成立當且僅當其平方成立。

反過來,當且僅當將兩邊都乘以非負數  和
和  後得到的等式成立。
後得到的等式成立。

並重寫為

是正確的。但將它分解為

表明這個結果是肯定正確的,因為它只是說明了向量  的長度的平方不為負數。
的長度的平方不為負數。
關於等式,它成立當且僅當  是
是  。檢查
。檢查  當且僅當一個向量是另一個向量的非負實數倍,很容易。
當且僅當一個向量是另一個向量的非負實數倍,很容易。
這個結果支援直覺,即即使在高維空間中,直線也是直的,平面也是平的。對於線性表面上的任意兩點,連線它們的線段都包含在該表面中(這很容易從定義中檢查出來)。但如果表面有彎曲,那麼就會有捷徑(這裡以灰色顯示,而從  到
到  的線段包含在表面中是實心的)。
的線段包含在表面中是實心的)。
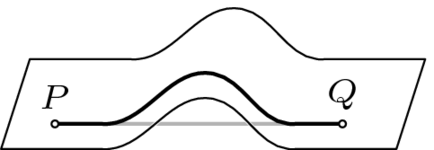
因為三角不等式指出,在任何  中,兩個端點之間最短的捷徑就是連線它們的線段,線性表面沒有這樣的彎曲。
中,兩個端點之間最短的捷徑就是連線它們的線段,線性表面沒有這樣的彎曲。
回到角測量的定義。三角不等式證明的核心是“ ” 行。乍一看,讀者可能會想知道是否有一些向量對以這種方式滿足不等式:當
” 行。乍一看,讀者可能會想知道是否有一些向量對以這種方式滿足不等式:當  是一個很大的數,其絕對值大於右邊的值,它是一個負的很大的數。下面的結果表明,不存在這樣的向量對。
是一個很大的數,其絕對值大於右邊的值,它是一個負的很大的數。下面的結果表明,不存在這樣的向量對。
- 推論 2.6(柯西-施瓦茨不等式)
對於任何  ,
,

當且僅當一個向量是另一個向量的標量倍時,等式成立。
- 證明
三角不等式的證明表明 ,所以如果
,所以如果 為正或零,則我們完成了。如果
為正或零,則我們完成了。如果 為負,則也成立。
為負,則也成立。

等式條件見問題 9。
柯西-施瓦茨不等式確保我們下一個定義是有意義的,因為分數的絕對值小於或等於 1。
- 定義 2.7
兩個非零向量 之間的夾角為
之間的夾角為

(零向量與任何其他向量之間的夾角定義為直角)。
因此,來自 的向量正交(或垂直)當且僅當它們的點積為零。
的向量正交(或垂直)當且僅當它們的點積為零。
- 示例 2.8
這些向量是正交的。

| 
|
箭頭顯示遠離規範位置,但向量仍然是正交的。
- 示例 2.9
本節開頭給出的 角公式是定義的特例。在這兩個之間
角公式是定義的特例。在這兩個之間
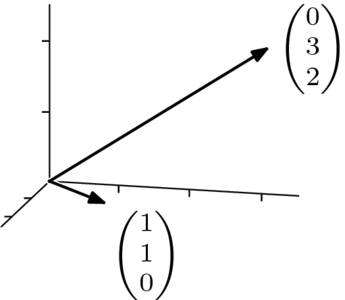
夾角為

大約為  。請注意,這些向量不垂直。儘管
。請注意,這些向量不垂直。儘管  -平面似乎垂直於
-平面似乎垂直於  -平面,但實際上,這兩個平面只是在弱意義上才是這樣,即每個平面中都有與另一個平面中所有向量都正交的向量。每個平面中並非所有向量都與另一個平面中所有向量正交。
-平面,但實際上,這兩個平面只是在弱意義上才是這樣,即每個平面中都有與另一個平面中所有向量都正交的向量。每個平面中並非所有向量都與另一個平面中所有向量正交。
- 建議所有讀者完成此練習。
- 建議所有讀者完成此練習。
- 建議所有讀者完成此練習。
- 問題 4
求 的值,使得這兩個向量垂直。
的值,使得這兩個向量垂直。

- 問題 5
描述在 中與該向量正交的向量的集合。
中與該向量正交的向量的集合。

- 建議所有讀者完成此練習。
- 問題 6
- 求
 中單位正方形的對角線與其中一條軸的夾角。
中單位正方形的對角線與其中一條軸的夾角。 - 求
 中單位立方體的對角線與其中一條軸的夾角。
中單位立方體的對角線與其中一條軸的夾角。 - 求
 中單位立方體的對角線與其中一條軸的夾角。
中單位立方體的對角線與其中一條軸的夾角。 - 當
 趨於
趨於 時,
時, 中單位立方體的對角線與其中一條軸的夾角的極限是多少?
中單位立方體的對角線與其中一條軸的夾角的極限是多少?
- 建議所有讀者完成此練習。
- 問題 8
描述點積的代數性質。
- 向量的點積對加法是否右分配律:
 ?
? - 向量的點積對加法是否左分配律(對加法)?
- 向量的點積是否滿足交換律?
- 向量的點積是否滿足結合律?
- 向量點積與標量乘法如何互動?
與往常一樣,任何斷言必須以證明或例子為依據。
- 建議所有讀者完成此練習。
- 問題 11
除了零向量,還有其他長度為零的向量嗎?(如果“是”,請給出例子。如果“否”,請證明。)
- 建議所有讀者完成此練習。
- 建議所有讀者完成此練習。
- 問題 15
長度為 1 的向量  被稱為單位向量。證明兩個單位向量的點積的絕對值小於或等於 1。 "小於" 可能嗎?"等於" 可能嗎?
被稱為單位向量。證明兩個單位向量的點積的絕對值小於或等於 1。 "小於" 可能嗎?"等於" 可能嗎?
- 問題 16
證明 
- 問題 18
是否  ?如果成立,它將推廣三角不等式。
?如果成立,它將推廣三角不等式。
- 問題 19
柯西-施瓦茨不等式中兩邊之間的比率是多少?
- 問題 21
描述 中兩個向量之間的角度。
中兩個向量之間的角度。
- 問題 22
給出一個簡單的充要條件來確定兩個向量之間的角度是銳角、直角還是鈍角。
- 建議所有讀者完成此練習。
- 問題 25
證明如果一個向量垂直於另外兩個向量中的每一個,那麼它就垂直於它們生成的平面上的每個向量。(備註。它們可以生成一個退化的平面——一條線或一個點——但該陳述仍然成立。)
- 問題 26
證明,其中 是非零向量,向量
是非零向量,向量

平分它們之間的角度。在 中說明。
中說明。
- 建議所有讀者完成此練習。
- 建議所有讀者完成此練習。
- 問題 31
首先證明拉格朗日恆等式,然後驗證柯西-施瓦茨不等式

然後注意到最後一項是正的。(回憶一下意思

和

的  符號。)此結果比柯西-施瓦茨不等式有所改進,因為它給出了兩邊差值的公式。在
符號。)此結果比柯西-施瓦茨不等式有所改進,因為它給出了兩邊差值的公式。在  中解釋該差值。
中解釋該差值。
解決方案
- O'Hanian, Hans (1985), Physics, vol. 1, W. W. Norton
- Ivanoff, V. F. (proposer); Esty, T. C. (solver) (1933), "Problem 3529", American Mathematical Monthly, 39 (2): 118
- Pólya, G. (1954), Mathematics and Plausible Reasoning: Volume II Patterns of Plausible Inference, Princeton University Press






















































































































