"高維幾何"聽起來很奇特。它確實很奇特——有趣且令人大開眼界。但它並不遙不可及。
我們首先定義一維空間為集合  。為了看到這個定義是合理的,繪製一個一維空間
。為了看到這個定義是合理的,繪製一個一維空間

並進行與  的通常對應:選擇一個點標記為
的通常對應:選擇一個點標記為  ,另一個標記為
,另一個標記為  。
。

現在,有了刻度和方向,找到對應於例如  的點很容易——從
的點很容易——從  開始,沿著
開始,沿著  的方向(即正方向)前進,但不要停在那裡,繼續前進
的方向(即正方向)前進,但不要停在那裡,繼續前進  倍的距離。
倍的距離。
這裡的基本思想是將大小與方向結合起來,這是擴充套件到更高維度的關鍵。
由大小和方向組成的物件稱為向量(我們將使用與上一節相同的詞,因為我們將在下面展示如何用列向量描述這樣的物件)。我們可以將向量繪製為具有特定長度並指向某個方向。

這裡有一個微妙之處——這些向量

是相等的,即使它們起始位置不同,因為它們具有相等的長度和相等的方向。再說一次:這些向量不僅僅是相似,它們是相等的。
如何理解在不同位置的事物可以相等?將向量視為表示位移("向量"在拉丁語中意為 "載體" 或 "旅行者")。這些正方形經歷了相同的位移,儘管這些位移起始位置不同。

有時,為了強調向量不固定的特性,它們被稱為自由向量。因此,這些自由向量是相等的,因為每個向量都表示一個向右移動一個單位,向上移動兩個單位的位移。
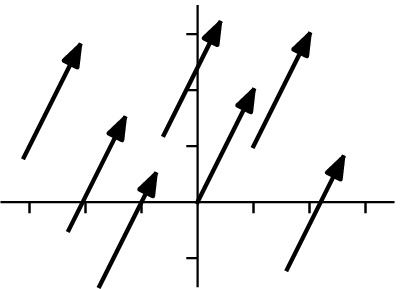
更一般地,平面上向量相等,當且僅當它們在第一分量上的變化相同,在第二分量上的變化也相同:從  指向
指向  的向量等於從
的向量等於從  指向
指向  的向量,當且僅當
的向量,當且僅當  且
且  。
。
像“從  開始的向量,如果它要延伸到
開始的向量,如果它要延伸到  ” 這樣的表達很笨拙。相反,我們將這樣的向量描述為
” 這樣的表達很笨拙。相反,我們將這樣的向量描述為

例如,上面顯示的“向右移動一個單位,向上移動兩個單位”的箭頭就描繪了這個向量。

我們通常將箭頭繪製為從原點開始,並稱其為規範位置(或自然位置)。當向量

處於其規範位置時,它延伸到端點  .
.
我們通常只提及“點
 "
"
”,而不是“該向量的規範位置的端點”。
因此,我們將這兩個集合都稱為  .
.

在上一節中,我們用代數的動機定義了向量和向量運算;

現在我們可以從幾何角度來解釋這些運算。例如,如果 代表一個位移,那麼
代表一個位移,那麼 代表一個方向相同但距離是其三倍的位移,而
代表一個方向相同但距離是其三倍的位移,而  代表一個與
代表一個與  相同距離但在相反方向的位移。
相同距離但在相反方向的位移。

並且,當  和
和  代表位移時,
代表位移時, 代表這兩個位移的組合。
代表這兩個位移的組合。
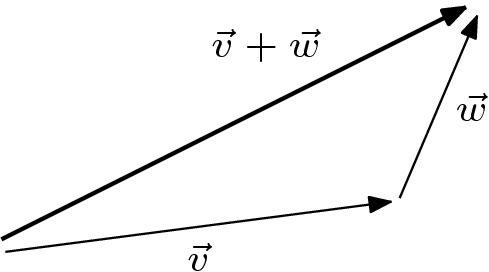
這條長箭頭表示這種意義上的組合位移:如果在一分鐘內,一艘船相對於地球的運動使它產生了  的位移,而一名乘客相對於船的甲板的運動產生了
的位移,而一名乘客相對於船的甲板的運動產生了  的位移,那麼
的位移,那麼  就是乘客相對於地球的位移。
就是乘客相對於地球的位移。
理解向量和的另一種方法是使用平行四邊形法則。畫出由向量  形成的平行四邊形,那麼和
形成的平行四邊形,那麼和  沿著對角線延伸到遠角。
沿著對角線延伸到遠角。
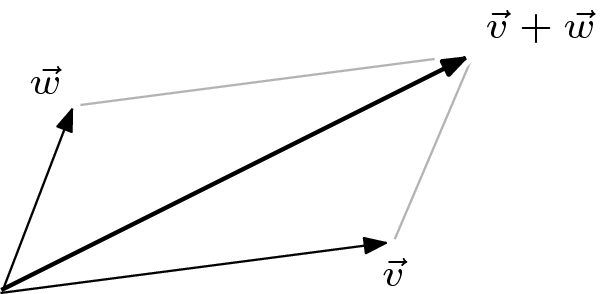
以上圖示展示了向量和向量運算在  中的行為。我們可以將這種行為擴充套件到
中的行為。我們可以將這種行為擴充套件到  ,甚至擴充套件到我們沒有影像的更高維空間,並進行明顯的推廣:如果一個自由向量從
,甚至擴充套件到我們沒有影像的更高維空間,並進行明顯的推廣:如果一個自由向量從  開始,在
開始,在  結束,那麼它可以用下面這列向量表示
結束,那麼它可以用下面這列向量表示

(向量相等如果它們有相同的表示),我們並不太在意區分一個點和以該點為終點的向量的規範表示,

加法和標量乘法都是按分量進行的。
我們已經考慮了點,現在轉向直線。
在  中,經過
中,經過  和
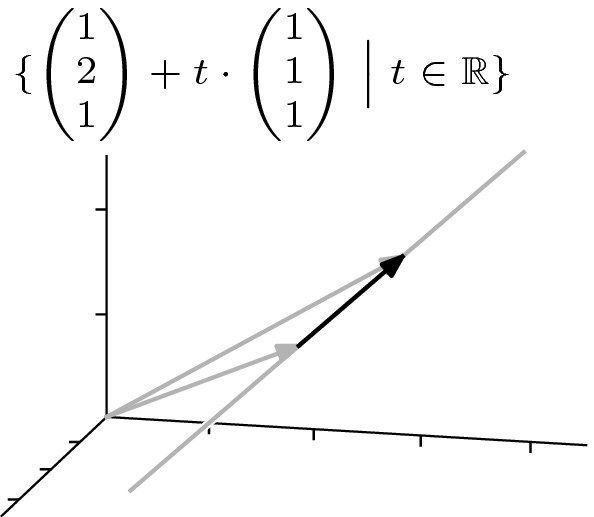
和  的直線包含(以下集合中向量的終點)
的直線包含(以下集合中向量的終點)

該描述表達了這幅圖。
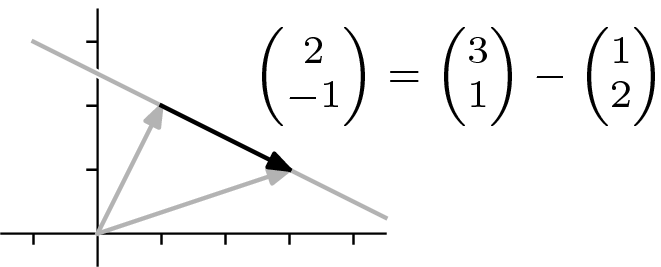
與引數  相關的向量在其整個主體都在直線上——它是一個方向向量,用於直線。請注意,直線上位於
相關的向量在其整個主體都在直線上——它是一個方向向量,用於直線。請注意,直線上位於  左側的點使用
左側的點使用  的負值來描述。
的負值來描述。
在  中,經過
中,經過  和
和  的直線是以下形式的向量集(向量終點)
的直線是以下形式的向量集(向量終點)
更高維空間中的直線也是以相同的方式工作的。
如果一條直線使用一個引數,因此可以在一個維度上自由移動,那麼一個平面必須包含兩個引數。例如,經過點  ,
, ,和
,和  的平面包含(以下集合中向量的終點)
的平面包含(以下集合中向量的終點)

(與引數相關的列向量

是兩個整個向量都在平面上的向量)。與直線一樣,請注意,這個平面中的某些點是用負數描述的  或負數
或負數  或兩者。
或兩者。
在代數和微積分中經常遇到的平面描述使用單個方程作為描述平面中點的一、二、三座標之間關係的條件。

從這種描述到我們在這本書中喜歡的向量描述的轉換是將條件視為一個方程線性系統,並將  引數化。
引數化。

從直線和平面的推廣,我們定義一個 維線性曲面(或
維線性曲面(或 平面)在
平面)在  中為
中為  ,其中
,其中  。例如,在
。例如,在  中,
中,

是一條直線,

是一個平面,以及

是一個三維線性曲面。同樣,直觀的理解是,直線允許在一個方向上運動,平面允許在兩個方向的組合上運動,等等。
線性曲面的描述可能會對維度產生誤導 - 這個

是一個退化的平面,因為它實際上是一條直線。

我們將在第二章的線性無關部分看到,向量之間的哪些關係會導致它們生成的線性曲面退化。
在本節的最後,我們將用幾何術語重新說明第一節的結論。首先,具有  個未知數的線性方程組的解集是
個未知數的線性方程組的解集是  中的線性曲面。具體來說,它是一個
中的線性曲面。具體來說,它是一個  維線性曲面,其中
維線性曲面,其中  是系統梯形形式中自由變數的個數。其次,齊次線性方程組的解集是經過原點的線性曲面。最後,我們可以將任何線性方程組的通解集看作是其關聯齊次方程組的解集從原點偏移一個向量,即任何特解。
是系統梯形形式中自由變數的個數。其次,齊次線性方程組的解集是經過原點的線性曲面。最後,我們可以將任何線性方程組的通解集看作是其關聯齊次方程組的解集從原點偏移一個向量,即任何特解。
- 此練習推薦所有讀者嘗試。
- 問題 1
找到每個向量的規範名稱。
- 從
 到
到  的向量,在
的向量,在  中。
中。 - 從
 到
到  的向量,在
的向量,在  中。
中。 - 從
 到
到  的向量,在
的向量,在  中。
中。 - 從
 到
到  的向量,在
的向量,在  中。
中。
- 此練習推薦所有讀者嘗試。
- 問題 2
判斷這兩個向量是否相等。
- 從
 到
到  的向量,和從
的向量,和從  到
到  的向量。
的向量。 - 從
 到
到  的向量,和從
的向量,和從  到
到  的向量。
的向量。
- 此練習推薦所有讀者嘗試。
- 問題 3
向量  是否位於透過
是否位於透過  和
和  的直線上?
的直線上?
- 此練習推薦所有讀者嘗試。
- 問題 4
- 描述透過
 ,
,  , 和
, 和  的平面。
的平面。 - 原點在這個平面上嗎?
- 問題 5
描述包含以下點和直線的平面。

- 此練習推薦所有讀者嘗試。
- 問題 6
找到這些平面的交點

- 此練習推薦所有讀者嘗試。
- 問題 7
如果可能,求解以下各對的交集。
-


-


- 問題 8
當一個平面不經過原點時,對位於平面內的向量的操作比平面經過原點時要複雜。請考慮本節中關於平面

以及它顯示的三個向量,其端點為  ,
,  , 以及
, 以及  .
.
- 重新繪製圖像,包括在平面內長度是具有終點
 的向量的兩倍的向量。你的向量的終點不是
的向量的兩倍的向量。你的向量的終點不是  ; 它是多少?
; 它是多少? - 重新繪製圖像,包括在平面內顯示以
 和
和  為終點的向量的和的平行四邊形。和的終點,在對角線上,不是
為終點的向量的和的平行四邊形。和的終點,在對角線上,不是  ; 它是多少?
; 它是多少?
- 問題 10
應該如何定義  ?
?
- 此練習推薦所有讀者嘗試。
- ?問題 11
一個人以  英里/小時的速度向東行駛,發現風似乎直接從北方吹來。當他的速度翻倍時,風似乎從東北方向吹來。風的速率是多少?(Klamkin 1957)
英里/小時的速度向東行駛,發現風似乎直接從北方吹來。當他的速度翻倍時,風似乎從東北方向吹來。風的速率是多少?(Klamkin 1957)
- 此練習推薦所有讀者嘗試。
- 問題 12
歐幾里得將平面描述為“一個與直線在自身上平行的表面”。註釋者(例如,希羅)將此解釋為“(平面表面)是這樣的,如果一條直線經過它的兩個點,這條直線在各個位置都與它完全重合,所有方向都是這樣”。(來自 Heath 1956 的翻譯,第 171-172 頁。)本節中描述的平面具有該特性嗎?這個描述是否充分定義了平面?
解答
- Klamkin, M. S. (proposer) (1957), "Trickie T-27", Mathematics Magazine, 30 (3): 173 .
- Heath, T. (1956), Euclid's Elements, vol. 1, Dover.











































































































