在之前的小節中,我們已經用線性對映的加法和標量乘法來表示線性對映,接下來自然要考慮的對映操作是複合。
為了瞭解複合的表示是如何從兩個複合物的表示中產生的,讓我們考慮一個例子。
- 示例 2.2
令  和
和  ,固定基
,固定基  ,
, ,
, ,並讓這些成為表示。
,並讓這些成為表示。

為了表示組合  ,我們固定一個
,我們固定一個  ,表示
,表示  的
的  ,然後表示
,然後表示  的那個。
的那個。  的表示是
的表示是  的矩陣和
的矩陣和  的向量的乘積。
的向量的乘積。

對
在 v {\displaystyle v}  上進行分配和重新分組,得到
上進行分配和重新分組,得到
- = ( ( 1 ⋅ 4 + 1 ⋅ 5 ) v 1 + ( 1 ⋅ 6 + 1 ⋅ 7 ) v 2 + ( 1 ⋅ 8 + 1 ⋅ 9 ) v 3 + ( 1 ⋅ 2 + 1 ⋅ 3 ) v 4 ( 0 ⋅ 4 + 1 ⋅ 5 ) v 1 + ( 0 ⋅ 6 + 1 ⋅ 7 ) v 2 + ( 0 ⋅ 8 + 1 ⋅ 9 ) v 3 + ( 0 ⋅ 2 + 1 ⋅ 3 ) v 4 ( 1 ⋅ 4 + 0 ⋅ 5 ) v 1 + ( 1 ⋅ 6 + 0 ⋅ 7 ) v 2 + ( 1 ⋅ 8 + 0 ⋅ 9 ) v 3 + ( 1 ⋅ 2 + 0 ⋅ 3 ) v 4 ) D {\displaystyle ={\begin{pmatrix}(1\cdot 4+1\cdot 5)v_{1}+(1\cdot 6+1\cdot 7)v_{2}+(1\cdot 8+1\cdot 9)v_{3}+(1\cdot 2+1\cdot 3)v_{4}\\(0\cdot 4+1\cdot 5)v_{1}+(0\cdot 6+1\cdot 7)v_{2}+(0\cdot 8+1\cdot 9)v_{3}+(0\cdot 2+1\cdot 3)v_{4}\\(1\cdot 4+0\cdot 5)v_{1}+(1\cdot 6+0\cdot 7)v_{2}+(1\cdot 8+0\cdot 9)v_{3}+(1\cdot 2+0\cdot 3)v_{4}\end{pmatrix}}_{D}}

我們將其識別為該矩陣-向量積的結果。
- = ( 1 ⋅ 4 + 1 ⋅ 5 1 ⋅ 6 + 1 ⋅ 7 1 ⋅ 8 + 1 ⋅ 9 1 ⋅ 2 + 1 ⋅ 3 0 ⋅ 4 + 1 ⋅ 5 0 ⋅ 6 + 1 ⋅ 7 0 ⋅ 8 + 1 ⋅ 9 0 ⋅ 2 + 1 ⋅ 3 1 ⋅ 4 + 0 ⋅ 5 1 ⋅ 6 + 0 ⋅ 7 1 ⋅ 8 + 0 ⋅ 9 1 ⋅ 2 + 0 ⋅ 3 ) B , D ( v 1 v 2 v 3 v 4 ) D {\displaystyle ={\begin{pmatrix}1\cdot 4+1\cdot 5&1\cdot 6+1\cdot 7&1\cdot 8+1\cdot 9&1\cdot 2+1\cdot 3\\0\cdot 4+1\cdot 5&0\cdot 6+1\cdot 7&0\cdot 8+1\cdot 9&0\cdot 2+1\cdot 3\\1\cdot 4+0\cdot 5&1\cdot 6+0\cdot 7&1\cdot 8+0\cdot 9&1\cdot 2+0\cdot 3\end{pmatrix}}_{B,D}{\begin{pmatrix}v_{1}\\v_{2}\\v_{3}\\v_{4}\end{pmatrix}}_{D}}

因此,表示 g ∘ h {\displaystyle g\circ h}  的矩陣具有 G {\displaystyle G}
的矩陣具有 G {\displaystyle G}  的行與 H {\displaystyle H}
的行與 H {\displaystyle H}  的列組合在一起。
的列組合在一起。
- 定義 2.3
m × r {\displaystyle m\!\times \!r}  矩陣 G {\displaystyle G}
矩陣 G {\displaystyle G}  和 r × n {\displaystyle r\!\times \!n}
和 r × n {\displaystyle r\!\times \!n}  矩陣 H {\displaystyle H}
矩陣 H {\displaystyle H}  的矩陣乘積 是 m × n {\displaystyle m\!\times \!n}
的矩陣乘積 是 m × n {\displaystyle m\!\times \!n}  矩陣 P {\displaystyle P}
矩陣 P {\displaystyle P}  ,其中
,其中
- p i , j = g i , 1 h 1 , j + g i , 2 h 2 , j + ⋯ + g i , r h r , j {\displaystyle p_{i,j}=g_{i,1}h_{1,j}+g_{i,2}h_{2,j}+\dots +g_{i,r}h_{r,j}}

也就是說, i , j {\displaystyle i,j}  -th entry of the product is the dot product of the i {\displaystyle i}
-th entry of the product is the dot product of the i {\displaystyle i}  -th row and the j {\displaystyle j}
-th row and the j {\displaystyle j}  -th column.
-th column.
- G H = ( ⋮ g i , 1 g i , 2 … g i , r ⋮ ) ( h 1 , j … h 2 , j … ⋮ h r , j ) = ( ⋮ … p i , j … ⋮ ) {\displaystyle GH={\begin{pmatrix}&\vdots \\g_{i,1}&g_{i,2}&\ldots &g_{i,r}\\&\vdots \end{pmatrix}}{\begin{pmatrix}&h_{1,j}\\\ldots &h_{2,j}&\ldots \\&\vdots \\&h_{r,j}\end{pmatrix}}={\begin{pmatrix}&\vdots \\\ldots &p_{i,j}&\ldots \\&\vdots \end{pmatrix}}}

- 示例 2.4
來自 示例 2.2 的矩陣以這種方式組合。
- ( 1 ⋅ 4 + 1 ⋅ 5 1 ⋅ 6 + 1 ⋅ 7 1 ⋅ 8 + 1 ⋅ 9 1 ⋅ 2 + 1 ⋅ 3 0 ⋅ 4 + 1 ⋅ 5 0 ⋅ 6 + 1 ⋅ 7 0 ⋅ 8 + 1 ⋅ 9 0 ⋅ 2 + 1 ⋅ 3 1 ⋅ 4 + 0 ⋅ 5 1 ⋅ 6 + 0 ⋅ 7 1 ⋅ 8 + 0 ⋅ 9 1 ⋅ 2 + 0 ⋅ 3 ) = ( 9 13 17 5 5 7 9 3 4 6 8 2 ) {\displaystyle {\begin{pmatrix}1\cdot 4+1\cdot 5&1\cdot 6+1\cdot 7&1\cdot 8+1\cdot 9&1\cdot 2+1\cdot 3\\0\cdot 4+1\cdot 5&0\cdot 6+1\cdot 7&0\cdot 8+1\cdot 9&0\cdot 2+1\cdot 3\\1\cdot 4+0\cdot 5&1\cdot 6+0\cdot 7&1\cdot 8+0\cdot 9&1\cdot 2+0\cdot 3\end{pmatrix}}={\begin{pmatrix}9&13&17&5\\5&7&9&3\\4&6&8&2\end{pmatrix}}}

- 示例 2.5
- ( 2 0 4 6 8 2 ) ( 1 3 5 7 ) = ( 2 ⋅ 1 + 0 ⋅ 5 2 ⋅ 3 + 0 ⋅ 7 4 ⋅ 1 + 6 ⋅ 5 4 ⋅ 3 + 6 ⋅ 7 8 ⋅ 1 + 2 ⋅ 5 8 ⋅ 3 + 2 ⋅ 7 ) = ( 2 6 34 54 18 38 ) {\displaystyle {\begin{pmatrix}2&0\\4&6\\8&2\end{pmatrix}}{\begin{pmatrix}1&3\\5&7\end{pmatrix}}={\begin{pmatrix}2\cdot 1+0\cdot 5&2\cdot 3+0\cdot 7\\4\cdot 1+6\cdot 5&4\cdot 3+6\cdot 7\\8\cdot 1+2\cdot 5&8\cdot 3+2\cdot 7\end{pmatrix}}={\begin{pmatrix}2&6\\34&54\\18&38\end{pmatrix}}}

- 定理 2.6
線性對映的組合由代表的矩陣乘積表示。
- 證明
(該論點與例 2.2類似。) 假設 h : V → W {\displaystyle h:V\to W}  和 g : W → X {\displaystyle g:W\to X}
和 g : W → X {\displaystyle g:W\to X}  分別由 H {\displaystyle H}
分別由 H {\displaystyle H}  和 G {\displaystyle G}
和 G {\displaystyle G}  表示,分別對應基底 B ⊂ V {\displaystyle B\subset V}
表示,分別對應基底 B ⊂ V {\displaystyle B\subset V}  , C ⊂ W {\displaystyle C\subset W}
, C ⊂ W {\displaystyle C\subset W}  和 D ⊂ X {\displaystyle D\subset X}
和 D ⊂ X {\displaystyle D\subset X}  ,大小分別為 n {\displaystyle n}
,大小分別為 n {\displaystyle n}  , r {\displaystyle r}
, r {\displaystyle r}  和 m {\displaystyle m}
和 m {\displaystyle m}  。對於任何 v → ∈ V {\displaystyle {\vec {v}}\in V}
。對於任何 v → ∈ V {\displaystyle {\vec {v}}\in V}  , R e p C ( h ( v → ) ) {\displaystyle {\rm {Rep}}_{C}(\,h({\vec {v}})\,)}
, R e p C ( h ( v → ) ) {\displaystyle {\rm {Rep}}_{C}(\,h({\vec {v}})\,)}  的第 k {\displaystyle k}
的第 k {\displaystyle k}  個分量是
個分量是
- h k , 1 v 1 + ⋯ + h k , n v n {\displaystyle h_{k,1}v_{1}+\cdots +h_{k,n}v_{n}}

因此, R e p D ( g ∘ h ( v → ) ) {\displaystyle {\rm {Rep}}_{D}(\,g\circ h\,({\vec {v}})\,)}  的第 i {\displaystyle i}
的第 i {\displaystyle i}  個分量是:
個分量是:
- g i , 1 ⋅ ( h 1 , 1 v 1 + ⋯ + h 1 , n v n ) + g i , 2 ⋅ ( h 2 , 1 v 1 + ⋯ + h 2 , n v n ) {\displaystyle g_{i,1}\cdot (h_{1,1}v_{1}+\dots +h_{1,n}v_{n})+g_{i,2}\cdot (h_{2,1}v_{1}+\dots +h_{2,n}v_{n})}

- + ⋯ + g i , r ⋅ ( h r , 1 v 1 + ⋯ + h r , n v n ) {\displaystyle +\dots +g_{i,r}\cdot (h_{r,1}v_{1}+\dots +h_{r,n}v_{n})}

將 v {\displaystyle v}  進行分配並重新分組。
進行分配並重新分組。
- = ( g i , 1 h 1 , 1 + g i , 2 h 2 , 1 + ⋯ + g i , r h r , 1 ) ⋅ v 1 {\displaystyle =(g_{i,1}h_{1,1}+g_{i,2}h_{2,1}+\dots +g_{i,r}h_{r,1})\cdot v_{1}}

- + ⋯ + ( g i , 1 h 1 , n + g i , 2 h 2 , n + ⋯ + g i , r h r , n ) ⋅ v n {\displaystyle +\dots +(g_{i,1}h_{1,n}+g_{i,2}h_{2,n}+\dots +g_{i,r}h_{r,n})\cdot v_{n}}

最後,注意到每個 v j {\displaystyle v_{j}}  的係數
的係數
- g i , 1 h 1 , j + g i , 2 h 2 , j + ⋯ + g i , r h r , j {\displaystyle g_{i,1}h_{1,j}+g_{i,2}h_{2,j}+\dots +g_{i,r}h_{r,j}}

與乘積 G H {\displaystyle GH}  中 i , j {\displaystyle i,j}
中 i , j {\displaystyle i,j}  項的定義相符。
項的定義相符。
該定理是支援定義的結果的一個例子。我們可以用這個 **箭頭圖** 來描繪定義和定理一起表達的內容(“wrt” 代表“相對於”)。
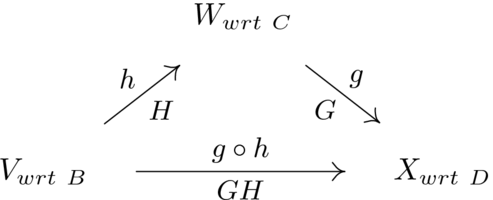
箭頭上方,對映表明從 V {\displaystyle V}  到 X {\displaystyle X}
到 X {\displaystyle X}  的兩種方式,直接透過合成或透過 W {\displaystyle W}
的兩種方式,直接透過合成或透過 W {\displaystyle W}  ,具有相同的效果。
,具有相同的效果。
- v → ⟼ g ∘ h g ( h ( v → ) ) v → ⟼ h h ( v → ) ⟼ g g ( h ( v → ) ) {\displaystyle {\vec {v}}{\stackrel {g\circ h}{\longmapsto }}g(h({\vec {v}}))\qquad {\vec {v}}{\stackrel {h}{\longmapsto }}h({\vec {v}}){\stackrel {g}{\longmapsto }}g(h({\vec {v}}))}

(這僅僅是複合的定義)。箭頭下方,矩陣表示產品執行相同的操作——將 G H {\displaystyle GH}  乘以列向量 R e p B ( v → ) {\displaystyle {\rm {Rep}}_{B}({\vec {v}})}
乘以列向量 R e p B ( v → ) {\displaystyle {\rm {Rep}}_{B}({\vec {v}})}  與首先將列向量乘以 H {\displaystyle H}
與首先將列向量乘以 H {\displaystyle H}  ,然後將結果乘以 G {\displaystyle G}
,然後將結果乘以 G {\displaystyle G}  具有相同的效果。
具有相同的效果。
- R e p B , D ( g ∘ h ) = G H = R e p C , D ( g ) R e p B , C ( h ) {\displaystyle {\rm {Rep}}_{B,D}(g\circ h)=GH={\rm {Rep}}_{C,D}(g)\,{\rm {Rep}}_{B,C}(h)}

矩陣乘法運算的定義並沒有限制我們將其視為線性映射覆合的表示。我們可以透過將其作為一種機械程式進行研究來深入瞭解這種操作。令人驚奇的是,行和列是如何結合的。
這種結合的一個方面是所涉及矩陣的大小非常重要。簡單來說, m × r times r × n equals m × n {\displaystyle m\!\times \!r{\text{ times }}r\!\times \!n{\text{ equals }}m\!\times \!n}  .
.
- 示例 2.7
這個乘法沒有定義
- ( − 1 2 0 0 10 1.1 ) ( 0 0 0 2 ) {\displaystyle {\begin{pmatrix}-1&2&0\\0&10&1.1\end{pmatrix}}{\begin{pmatrix}0&0\\0&2\end{pmatrix}}}

因為左側的列數不等於右側的行數。
就底層對映而言,大小必須匹配這一事實反映了矩陣乘法僅在相應的函式複合
- dimension n space ⟶ h dimension r space ⟶ g dimension m space {\displaystyle {\text{dimension }}n{\text{ space}}\;{\stackrel {h}{\longrightarrow }}\;{\text{dimension }}r{\text{ space}}\;{\stackrel {g}{\longrightarrow }}\;{\text{dimension }}m{\text{ space}}}

是可能的。
矩陣乘法運算中行和列組合方式的另一個方面是,在 i , j {\displaystyle i,j}  項的定義中
項的定義中
- p i , j = g i , 1 h 1 , j + g i , 2 h 2 , j + ⋯ + g i , r h r , j {\displaystyle p_{i,j}=g_{i,{\color {red}1}}h_{{\color {red}1},j}+g_{i,{\color {red}2}}h_{{\color {red}2},j}+\dots +g_{i,{\color {red}r}}h_{{\color {red}r},j}}

g {\displaystyle g}  上的紅色下標是列指示符,而 h {\displaystyle h}
上的紅色下標是列指示符,而 h {\displaystyle h}  上的紅色下標表示行。也就是說,求和是在 G {\displaystyle G}
上的紅色下標表示行。也就是說,求和是在 G {\displaystyle G}  的列上進行,但在 H {\displaystyle H}
的列上進行,但在 H {\displaystyle H}  的行上進行;左側的處理方式與右側不同,因此 G H {\displaystyle GH}
的行上進行;左側的處理方式與右側不同,因此 G H {\displaystyle GH}  可能不等於 H G {\displaystyle HG}
可能不等於 H G {\displaystyle HG}  。矩陣乘法不滿足交換律。
。矩陣乘法不滿足交換律。
- 示例 2.9
矩陣乘法幾乎從不滿足交換律。透過以兩種方式相乘隨機選擇的矩陣來測試這一點。
- ( 1 2 3 4 ) ( 5 6 7 8 ) = ( 19 22 43 50 ) ( 5 6 7 8 ) ( 1 2 3 4 ) = ( 23 34 31 46 ) {\displaystyle {\begin{pmatrix}1&2\\3&4\end{pmatrix}}{\begin{pmatrix}5&6\\7&8\end{pmatrix}}={\begin{pmatrix}19&22\\43&50\end{pmatrix}}\qquad {\begin{pmatrix}5&6\\7&8\end{pmatrix}}{\begin{pmatrix}1&2\\3&4\end{pmatrix}}={\begin{pmatrix}23&34\\31&46\end{pmatrix}}}

- 示例 2.10
交換律失效的情況可能更加嚴重
- ( 5 6 7 8 ) ( 1 2 0 3 4 0 ) = ( 23 34 0 31 46 0 ) {\displaystyle {\begin{pmatrix}5&6\\7&8\end{pmatrix}}{\begin{pmatrix}1&2&0\\3&4&0\end{pmatrix}}={\begin{pmatrix}23&34&0\\31&46&0\end{pmatrix}}}

然而
- ( 1 2 0 3 4 0 ) ( 5 6 7 8 ) {\displaystyle {\begin{pmatrix}1&2&0\\3&4&0\end{pmatrix}}{\begin{pmatrix}5&6\\7&8\end{pmatrix}}}

甚至都沒有定義。
除了不滿足交換律外,矩陣乘法在代數上表現良好。以下是一些不錯的性質,更多性質可以在 習題 10 和 習題 11 中找到。
- 注 2.13
我們也可以透過繁瑣的索引運算來證明這個結果。例如,結合律可以寫成: ( F G ) H {\displaystyle (FG)H}  的第 i , j {\displaystyle i,j}
的第 i , j {\displaystyle i,j}  個元素是
個元素是
- ( f i , 1 g 1 , 1 + f i , 2 g 2 , 1 + ⋯ + f i , r g r , 1 ) h 1 , j + ( f i , 1 g 1 , 2 + f i , 2 g 2 , 2 + ⋯ + f i , r g r , 2 ) h 2 , j ⋮ + ( f i , 1 g 1 , s + f i , 2 g 2 , s + ⋯ + f i , r g r , s ) h s , j {\displaystyle {\begin{array}{rl}&(f_{i,1}g_{1,1}+f_{i,2}g_{2,1}+\dots +f_{i,r}g_{r,1})h_{1,j}\\&\quad +(f_{i,1}g_{1,2}+f_{i,2}g_{2,2}+\dots +f_{i,r}g_{r,2})h_{2,j}\\&\quad \;\;\vdots \\&\quad +(f_{i,1}g_{1,s}+f_{i,2}g_{2,s}+\dots +f_{i,r}g_{r,s})h_{s,j}\end{array}}}

(其中 F {\displaystyle F}  , G {\displaystyle G}
, G {\displaystyle G}  和 H {\displaystyle H}
和 H {\displaystyle H}  是 m × r {\displaystyle m\!\times \!r}
是 m × r {\displaystyle m\!\times \!r}  , r × s {\displaystyle r\!\times \!s}
, r × s {\displaystyle r\!\times \!s}  和 s × n {\displaystyle s\!\times \!n}
和 s × n {\displaystyle s\!\times \!n}  矩陣),分配
矩陣),分配
- f i , 1 g 1 , 1 h 1 , j + f i , 2 g 2 , 1 h 1 , j + ⋯ + f i , r g r , 1 h 1 , j + f i , 1 g 1 , 2 h 2 , j + f i , 2 g 2 , 2 h 2 , j + ⋯ + f i , r g r , 2 h 2 , j ⋮ + f i , 1 g 1 , s h s , j + f i , 2 g 2 , s h s , j + ⋯ + f i , r g r , s h s , j {\displaystyle {\begin{array}{rl}&f_{i,1}g_{1,1}h_{1,j}+f_{i,2}g_{2,1}h_{1,j}+\dots +f_{i,r}g_{r,1}h_{1,j}\\&\quad +f_{i,1}g_{1,2}h_{2,j}+f_{i,2}g_{2,2}h_{2,j}+\dots +f_{i,r}g_{r,2}h_{2,j}\\&\quad \;\;\vdots \\&\quad +f_{i,1}g_{1,s}h_{s,j}+f_{i,2}g_{2,s}h_{s,j}+\dots +f_{i,r}g_{r,s}h_{s,j}\end{array}}}

並圍繞 f {\displaystyle f}  進行重新分組
進行重新分組
- f i , 1 ( g 1 , 1 h 1 , j + g 1 , 2 h 2 , j + ⋯ + g 1 , s h s , j ) + f i , 2 ( g 2 , 1 h 1 , j + g 2 , 2 h 2 , j + ⋯ + g 2 , s h s , j ) ⋮ + f i , r ( g r , 1 h 1 , j + g r , 2 h 2 , j + ⋯ + g r , s h s , j ) {\displaystyle {\begin{array}{rl}&f_{i,1}(g_{1,1}h_{1,j}+g_{1,2}h_{2,j}+\dots +g_{1,s}h_{s,j})\\&\quad +f_{i,2}(g_{2,1}h_{1,j}+g_{2,2}h_{2,j}+\dots +g_{2,s}h_{s,j})\\&\quad \;\;\vdots \\&\quad +f_{i,r}(g_{r,1}h_{1,j}+g_{r,2}h_{2,j}+\dots +g_{r,s}h_{s,j})\end{array}}}

以獲得 i , j {\displaystyle i,j}  的 F ( G H ) {\displaystyle F(GH)}
的 F ( G H ) {\displaystyle F(GH)}  項。
項。
對比驗證結合律的兩種方法,一種是在證明中,另一種是在上面。上面的論證很難理解,因為雖然計算很容易檢查,但算術似乎與任何想法都沒有聯絡(它也基本上重複了 定理 2.6 的證明,因此效率低下)。證明中的論證更短、更清晰,並說明了這種性質“真正”成立的原因。這說明了在向量空間章節前言中提到的評論——至少在某些情況下,來自更高層次結構的論證更清晰。
我們現在已經瞭解瞭如何從兩個線性對映的表示中推匯出它們組合的表示。我們稱這個組合為兩個矩陣的乘積。這種運算極其重要。在我們繼續研究如何表示線性對映的逆之前,我們將在下一小節中進一步探討它。
- 本練習建議所有讀者完成。
- 本練習建議所有讀者完成。
- 本練習建議所有讀者完成。
- 本練習建議所有讀者完成。
- 問題 5
找到從以下開始得到的方程組
- h 1 , 1 x 1 + h 1 , 2 x 2 + h 1 , 3 x 3 = d 1 h 2 , 1 x 1 + h 2 , 2 x 2 + h 2 , 3 x 3 = d 2 {\displaystyle {\begin{array}{*{3}{rc}r}h_{1,1}x_{1}&+&h_{1,2}x_{2}&+&h_{1,3}x_{3}&=&d_{1}\\h_{2,1}x_{1}&+&h_{2,2}x_{2}&+&h_{2,3}x_{3}&=&d_{2}\end{array}}}

並進行此變數更改(即替換)。
- x 1 = g 1 , 1 y 1 + g 1 , 2 y 2 x 2 = g 2 , 1 y 1 + g 2 , 2 y 2 x 3 = g 3 , 1 y 1 + g 3 , 2 y 2 {\displaystyle {\begin{array}{*{2}{rc}r}x_{1}&=&g_{1,1}y_{1}&+&g_{1,2}y_{2}\\x_{2}&=&g_{2,1}y_{1}&+&g_{2,2}y_{2}\\x_{3}&=&g_{3,1}y_{1}&+&g_{3,2}y_{2}\end{array}}}

- 問題 6
正如定義 2.3 指出,矩陣乘法運算概括了點積。一個 1 × n {\displaystyle 1\!\times \!n}  行向量和一個 n × 1 {\displaystyle n\!\times \!1}
行向量和一個 n × 1 {\displaystyle n\!\times \!1}  列向量的點積是否與其矩陣乘積相同?
列向量的點積是否與其矩陣乘積相同?
- 本練習建議所有讀者完成。
- 問題 8
證明在 R 1 {\displaystyle \mathbb {R} ^{1}}  上的線性變換的複合運算滿足交換律。這對於任何一維空間都成立嗎?
上的線性變換的複合運算滿足交換律。這對於任何一維空間都成立嗎?
- 問題 9
為什麼矩陣乘法不定義為逐元素乘法?這樣會更容易,而且也滿足交換律。
- 本練習建議所有讀者完成。
- 問題 10
- 證明 H p H q = H p + q {\displaystyle H^{p}H^{q}=H^{p+q}}
 且 ( H p ) q = H p q {\displaystyle (H^{p})^{q}=H^{pq}}
且 ( H p ) q = H p q {\displaystyle (H^{p})^{q}=H^{pq}}  對於正整數 p , q {\displaystyle p,q}
對於正整數 p , q {\displaystyle p,q}  成立。
成立。 - 證明 ( r H ) p = r p ⋅ H p {\displaystyle (rH)^{p}=r^{p}\cdot H^{p}}
 對於任何正整數 p {\displaystyle p}
對於任何正整數 p {\displaystyle p}  和標量 r ∈ R {\displaystyle r\in \mathbb {R} }
和標量 r ∈ R {\displaystyle r\in \mathbb {R} }  成立。
成立。
- 本練習建議所有讀者完成。
- 問題 11
- 矩陣乘法如何與標量乘法互動: r ( G H ) = ( r G ) H {\displaystyle r(GH)=(rG)H}
 嗎? G ( r H ) = r ( G H ) {\displaystyle G(rH)=r(GH)}
嗎? G ( r H ) = r ( G H ) {\displaystyle G(rH)=r(GH)}  嗎?
嗎? - 矩陣乘法如何與線性組合互動: F ( r G + s H ) = r ( F G ) + s ( F H ) {\displaystyle F(rG+sH)=r(FG)+s(FH)}
 嗎? ( r F + s G ) H = r F H + s G H {\displaystyle (rF+sG)H=rFH+sGH}
嗎? ( r F + s G ) H = r F H + s G H {\displaystyle (rF+sG)H=rFH+sGH}  嗎?
嗎?
- 本練習建議所有讀者完成。
- 問題 13
在 R 3 {\displaystyle \mathbb {R} ^{3}}  中繞某個軸旋轉向量是一個線性對映。證明線性對映不滿足交換律,方法是幾何地證明旋轉不滿足交換律。
中繞某個軸旋轉向量是一個線性對映。證明線性對映不滿足交換律,方法是幾何地證明旋轉不滿足交換律。
- 問題 14
在 定理 2.12 的證明中,使用了一些對映。這些對映的定義域和值域是什麼?
- 問題 15
矩陣秩如何與矩陣乘法互動?
- 兩個秩為 n {\displaystyle n}
 的矩陣的乘積的秩可以小於 n {\displaystyle n}
的矩陣的乘積的秩可以小於 n {\displaystyle n}  嗎?可以大於嗎?
嗎?可以大於嗎? - 證明兩個矩陣的乘積的秩小於等於每個因子的秩的最小值。
- 問題 16
“與…交換”在 n × n {\displaystyle n\!\times \!n}  矩陣中是等價關係嗎?
矩陣中是等價關係嗎?
- 本練習建議所有讀者完成。
- 問題 18
證明,對於方陣, ( S + T ) ( S − T ) {\displaystyle (S+T)(S-T)}  不一定等於 S 2 − T 2 {\displaystyle S^{2}-T^{2}}
不一定等於 S 2 − T 2 {\displaystyle S^{2}-T^{2}}  。
。
- 本練習建議所有讀者完成。
- 問題 21
- 證明對於任何 2 × 2 {\displaystyle 2\!\times \!2}
 矩陣 T {\displaystyle T}
矩陣 T {\displaystyle T}  ,存在標量 c 0 , … , c 4 {\displaystyle c_{0},\dots ,c_{4}}
,存在標量 c 0 , … , c 4 {\displaystyle c_{0},\dots ,c_{4}}  且不全為 0 {\displaystyle 0}
且不全為 0 {\displaystyle 0}  ,使得組合 c 4 T 4 + c 3 T 3 + c 2 T 2 + c 1 T + c 0 I {\displaystyle c_{4}T^{4}+c_{3}T^{3}+c_{2}T^{2}+c_{1}T+c_{0}I}
,使得組合 c 4 T 4 + c 3 T 3 + c 2 T 2 + c 1 T + c 0 I {\displaystyle c_{4}T^{4}+c_{3}T^{3}+c_{2}T^{2}+c_{1}T+c_{0}I}  為零矩陣(其中 I {\displaystyle I}
為零矩陣(其中 I {\displaystyle I}  是 2 × 2 {\displaystyle 2\!\times \!2}
是 2 × 2 {\displaystyle 2\!\times \!2}  單位矩陣,其 1 , 1 {\displaystyle 1,1}
單位矩陣,其 1 , 1 {\displaystyle 1,1}  和 2 , 2 {\displaystyle 2,2}
和 2 , 2 {\displaystyle 2,2}  元素為 1 {\displaystyle 1}
元素為 1 {\displaystyle 1}  ,其餘元素為零;參見 習題 19)。
,其餘元素為零;參見 習題 19)。 - 令 p ( x ) {\displaystyle p(x)}
 是一個多項式 p ( x ) = c n x n + ⋯ + c 1 x + c 0 {\displaystyle p(x)=c_{n}x^{n}+\dots +c_{1}x+c_{0}}
是一個多項式 p ( x ) = c n x n + ⋯ + c 1 x + c 0 {\displaystyle p(x)=c_{n}x^{n}+\dots +c_{1}x+c_{0}}  。如果 T {\displaystyle T}
。如果 T {\displaystyle T}  是方陣,則定義 p ( T ) {\displaystyle p(T)}
是方陣,則定義 p ( T ) {\displaystyle p(T)}  為矩陣 c n T n + ⋯ + c 1 T + I {\displaystyle c_{n}T^{n}+\dots +c_{1}T+I}
為矩陣 c n T n + ⋯ + c 1 T + I {\displaystyle c_{n}T^{n}+\dots +c_{1}T+I}  (其中 I {\displaystyle I}
(其中 I {\displaystyle I}  是適當大小的單位矩陣)。證明對於任何方陣,都存在一個多項式,使得 p ( T ) {\displaystyle p(T)}
是適當大小的單位矩陣)。證明對於任何方陣,都存在一個多項式,使得 p ( T ) {\displaystyle p(T)}  為零矩陣。
為零矩陣。 - 方陣的最小多項式 m ( x ) {\displaystyle m(x)}
 是使得 m ( T ) {\displaystyle m(T)}
是使得 m ( T ) {\displaystyle m(T)}  為零矩陣的,最低次且首項係數為 1 {\displaystyle 1}
為零矩陣的,最低次且首項係數為 1 {\displaystyle 1}  的多項式。求此矩陣的最小多項式。
的多項式。求此矩陣的最小多項式。- ( 3 / 2 − 1 / 2 1 / 2 3 / 2 ) {\displaystyle {\begin{pmatrix}{\sqrt {3}}/2&-1/2\\1/2&{\sqrt {3}}/2\end{pmatrix}}}

(這是關於 E 2 , E 2 {\displaystyle {\mathcal {E}}_{2},{\mathcal {E}}_{2}}  ,標準基,關於 π / 6 {\displaystyle \pi /6}
,標準基,關於 π / 6 {\displaystyle \pi /6}  弧度的逆時針旋轉的表示。)
弧度的逆時針旋轉的表示。)
- 問題 23
回想一下 a 1 , a 2 , … , a n {\displaystyle a_{1},a_{2},\dots ,a_{n}}  數字序列的求和符號。
數字序列的求和符號。
- ∑ i = 1 n a i = a 1 + a 2 + ⋯ + a n {\displaystyle \sum _{i=1}^{n}a_{i}=a_{1}+a_{2}+\dots +a_{n}}

在這個符號中, i , j {\displaystyle i,j}  是 G {\displaystyle G}
是 G {\displaystyle G}  和 H {\displaystyle H}
和 H {\displaystyle H}  乘積的項是這個。
乘積的項是這個。
- p i , j = ∑ k = 1 r g i , k h k , j {\displaystyle p_{i,j}=\sum _{k=1}^{r}g_{i,k}h_{k,j}}

使用此符號,
- 重新證明矩陣乘法滿足結合律;
- 重新證明 定理 2.6。
解答








































































































































































