實分析/導數的應用

←微分

實分析 導數的應用

黎曼積分→

導數也用於定理中。儘管本章名為“導數的應用”，但以下定理在數學的整體應用中只起到與其他數學定理相同的應用作用。我們將介紹的以下定理側重於說明函式的特徵，這些特徵在識別方面非常有用。由於圖形分析使用不同的分析方法構建，因此此處介紹的定理只適用於函式。但是，本章討論的所有內容都具有圖形成分，本章可能會參考這些圖形成分以更輕鬆地建立聯絡。在實分析中，圖形解釋通常不足以作為證明。

高階導數

為了開始我們構建與函式相關的新的定理，我們首先必須明確說明微分的特徵，我們將在本章後面的部分中不時使用它。

假設 $f:\mathbb {R} \to \mathbb {R}$ 可微分

令 $f'(x)$ 對所有 $x\in \mathbb {R}$ 可微分。則 $f'(x)$ 的導數稱為 $f$ 的 **二階導數**，寫成 $f''(a)$ 。

我們已經說明可能存在二階導數，它是導數的導數。我們將進一步定義 **a 處的二階導數**，指的是僅在值 a 處對導數的求導。

類似地，我們可以定義 $f$ 的 **n^th 階導數**，寫成 $f^{(n)}(x)$

基礎定理

本節將首先介紹微分提供的一些有趣性質。此處介紹的概念將有助於更深入地瞭解後面的定理。在 上一章 中，您已經瞭解了能夠對函式求導意味著該點處連續的概念。請記住這一點，因為每個定理都將使用連續性提供的概念來證明其證明。

在本節中，我們將提供更多基礎知識。

最小值和最大值點

現在我們將介紹關於函式的兩個新概念，這兩個概念您可能已經熟悉。然後，我們將透過建立一個定理來證明它的存在。

定義

我們定義一個函式 $f$ 在區間 A 上的 **最大值點** 為

$\exists \alpha \in A:f(\alpha )\geq f(x)\quad \forall x\in A$

我們定義一個函式 $f$ 在區間 A 上的 **最小值點** 為

$\exists \zeta \in A:f(\zeta )\leq f(x)\quad \forall x\in A$

這兩個定義互為補充，因為它們指的是相反的不等式。

最小值點和最大值點存在定理

這個證明將透過將其與微分聯絡起來來證明最小值點和最大值點的定義，具體來說是透過以下陳述

定理 給定一個在 $(a,b)$ 上定義的函式 $f$ ，它在 $x$ 處可微且是最大值點或最小值點，則它在 $x$ 處的導數等於 0

證明很簡單：它呼叫微分的定義來斷言定理的結果。

證明給定定義函式的最大值點導數為 0

應用定義。請注意，變數 $h$ 是任何數字，只要它與 α 相加仍然在區間 $(a,b)$ 內。	$f(\alpha )\geq f(\alpha +h)$
代數操作	$f(\alpha +h)-f(\alpha )\leq 0$
除以 h，這意味著兩種情況，因為它可能是負數（這意味著不等式會改變！）	$h>0$	$h<0$
	${\frac {f(\alpha +h)-f(\alpha )}{h}}\leq 0$	${\frac {f(\alpha +h)-f(\alpha )}{h}}\geq 0$
應用單邊極限，如果對兩邊都應用（它是；0 的極限是 0），則在代數上是有效的	$\lim _{h\to 0^{+}}{\frac {f(\alpha +h)-f(\alpha )}{h}}\leq 0$	$\lim _{h\to 0^{-}}{\frac {f(\alpha +h)-f(\alpha )}{h}}\geq 0$
將單邊極限合併在一起形成一個完整的極限，這需要一個相等的極限才能有效。只有一個值相等：0。	$\lim _{h\to 0}{\frac {f(\alpha +h)-f(\alpha )}{h}}=0$
	$f'(\alpha )=0$
$\blacksquare$

為了證明最小點的案例，你只需反轉初始不等式。請注意，證明仍然會產生相同的結果，即最小點的導數也是 0。

凸性和凹性

區間 $[x_{1},x_{2}]$ 上的凸函式示例

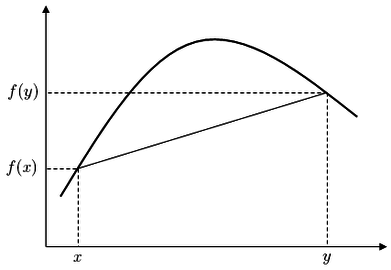區間 $[x,y]$ 上的凹函式示例

同樣地，我們現在將建立兩個與函式相關的更多互補定義。這些是凸性和凹性定義，一種根據函式與給定參考點（在本例中為直線）的關係來描述函式的方法。凸性和凹性反映了凸和凹的視覺、物理描述，儘管它們是根據直線如何從函式中突出而不是相反來描述的，因此在圖形上定義看起來是反轉的。

定義

我們將定義函式 $f$ 在區間 $A$ 上的**凸性**如下

給定 $A=[a,b]$ ，連線 $(a,f(a))$ 和 $(b,f(b))>f$ 的割線對所有 $x\in (a,b)$

我們將定義函式$f$在區間$A$上的凹性如下。

給定$A=[a,b]$，連線$(a,f(a))$和$(b,f(b))<f$的割線對於所有$x\in (a,b)$都位於函式下方。

如果將凸性的定義原封不動地拿來，數學描述將如下所示。

${\frac {f(b)-f(a)}{b-a}}(x-a)+f(a)>f(x)$

這種表達方式可以被改寫成另一種形式，雖然看起來更陌生，但更利於應用在定理中。

${\begin{aligned}{\dfrac {f(b)-f(a)}{b-a}}(x-a)+f(a)&>f(x)\\{\dfrac {f(b)-f(a)}{b-a}}(x-a)&>f(x)-f(a)\\{\dfrac {f(b)-f(a)}{b-a}}&>{\dfrac {f(x)-f(a)}{x-a}}\end{aligned}}$

同樣，凹性的定義只是將不等式反過來。

我們將在本章後續的凸性/凹性定理中使用這個定義。

推論

從這個定義得出的第一個推論是一個簡單卻經常不被解釋的，關於函式取反後的性質。

推論 給定一個在區間$A$上為凸函式的$f$，$-f$在區間$A$上為凹函式。

證明凸性是凹性的否定

應用凸性定義。	${\dfrac {f(b)-f(a)}{b-a}}<{\dfrac {f(x)-f(a)}{x-a}}$
假設其否定，經過一些代數運算後	${\begin{aligned}{\dfrac {f(b)-f(a)}{b-a}}&<{\dfrac {f(x)-f(a)}{x-a}}\\{\dfrac {-f(b)-(-f(a))}{b-a}}&<{\dfrac {-f(x)-(-f(a))}{x-a}}\\-{\dfrac {f(b)-f(a)}{b-a}}&<-{\dfrac {f(x)-f(a)}{x-a}}\end{aligned}}$
這是凹函式的定義。	${\dfrac {f(b)-f(a)}{b-a}}>{\dfrac {f(x)-f(a)}{x-a}}$
$\blacksquare$

函式的切線

從概念上講，求導數意味著求函式切線的斜率。因此，導數可以被看作是對函式的線性或一階近似。這可以透過使用 $f$ 在 $a$ 處的導數建立切線來圖形表示。使用以下公式，我們可以得到：

$y=\lim _{h\to 0}{\frac {f(a+h)-f(a)}{h}}(x-a)-f(a)$

透過函式操作，很明顯，這是一個平移到點 $(a,f(a))$ 的直線方程。

"微分產生切線" 定理

這個未命名的定理證明了我們之前對定義的理解沒有錯誤。利用這個定理，我們可以嚴格理解微分在圖形上的意義，即切線。這個定理是如此深入人心，以至於在上面的部分，我們定義了切線與微分的聯絡。在接下來的部分，我們將證明這個定理的有效性。

我們如何證明這個概念呢？我們將證明切線在物理上的意義：如果我們有一個完美的圓形表面，我們可以想象一根尺子放在上面，並且尺子只在一個點上平衡。這種物理描述意味著在其他地方都存在間隙，而這種“間隙”的概念將用切線與曲線函式值之間的不等式來表示。

定理 給定一個函式 $f$ 和一條穿過某一點 $(a,f(a))$ 的切線，這條切線除了 $(a,f(a))$ 以外，將始終大於或小於函式。

為了開始證明，我們首先要簡化問題併為我們的證明指定一個方向。總的來說，我們要 [ADD OVERALL OBJECTIVE OF PROOF]

現在，我們將指定一些情況，以便我們可以使用我們已知的屬性。

情況 1：凸函式

我們將要解決的第一個情況是，函式在某個區間$A$ 上是凸的。

凸函式切線存在的證明

假設我們對導數的定義進行動畫化。這意味著給定定義，我們分析 h 接近 0 時所有 h 的值。	${\dfrac {f(a+h)-f(a)}{h}}$
根據定義，這不是切線，而是割線。	${\dfrac {f(a+h_{1})-f(a)}{h_{1}}}<{\dfrac {f(b)-f(a)}{b-a}}$
	${\dfrac {f(a+h_{2})-f(a)}{h_{2}}}<{\dfrac {f(b)-f(a)}{b-a}}$
並且因為	${\dfrac {f(a+h_{1})-f(a)}{h_{1}}}<{\dfrac {f(b)-f(a)}{b-a}}$
	${\dfrac {f(a+h_{2})-f(a)}{h_{2}}}<{\dfrac {f(b)-f(a)}{b-a}}$

關於切線的定理

這三個定理都與切線如何與函式和圖形的交點相關聯。

羅爾定理

羅爾定理是導數的入門定理。這個證明將為本章中的許多其他證明開啟通道，尤其是下一節中發現的下一個重要的微分定理，中值定理。羅爾定理描述如下

定理 給定一個函式 $f:[a,b]\to \mathbb {R}$，它在 $[a,b]$ 上是連續的，在 $(a,b)$ 上是可微的，並且 $f(a)=f(b)$，那麼存在 $c\in (a,b)$ 使得 $f'(c)=0$

證明

我們將針對羅爾定理給出兩種證明。第一個利用最小值和最大值點存在定理，第二個利用反證法。

證明 1

首先，我們排除一個明顯的例子。如果函式 $f$ 是一個常數函式，則 $f'(x)=0\quad \forall x\in [a,b]$ 。 $\blacksquare$

如果函式 $f$ 不是一個常數函式，設 $\alpha \in [a,b]$ 使得 $f(c)=\sup f([a,b])$ 。換句話說，根據 最小-最大定理，我們知道在該連續函式中存在一個上確界。根據定義，該上確界模擬了最大點。

由於它模擬了最大點的定義，我們可以應用最小值和最大值點存在定理來證明語句 $f'(\alpha )=0$ 。

最小值的工作方式相同，只是我們會找到一個下確界而不是上確界，並且下確界的定義將與最小值點相匹配。最小值和最大值點存在定理仍然成立。

$\blacksquare$

證明 2

首先，我們排除一個明顯的例子。如果函式 $f$ 是一個常數函式，則 $f'(x)=0\quad \forall x\in [a,b]$ 。 $\blacksquare$

如果函式 $f$ 不是一個常數函式，設 $\alpha \in [a,b]$ 使得 $f(c)=\sup f([a,b])$ 。換句話說，根據 最小-最大定理，我們知道在該連續函式中存在一個上確界。根據定義，該上確界模擬了最大點。

不失一般性，我們可以說 $f(\alpha )>f(a)=f(b)$ 。換句話說，因為我們透過應用定理找到了一個大於函式中每個值的上確界，並且我們排除了函式是常數的情況，所以我們可以安全地斷言，根據定義，該上確界至少大於端點。

假設 $f'(c)>0$ 是有效的。因此，$\lim _{x\to c}{\frac {f(x)-f(c)}{x-c}}>0$ ，因此，存在 $x_{1}\in [a,b]$ 使得 $f(x_{1})>f(c)$ ，這與 $f(c)$ 是最大值的事實相矛盾。

類似地，我們可以證明假設 $f'(c)<0$ 會導致矛盾。因此，$f'(c)=0$ 。

$\blacksquare$

中值定理

該定理是羅爾定理的更強版本。定理的陳述如下：

定理 給定一個函式 $f:[a,b]\to \mathbb {R}$ ，該函式在 $[a,b]$ 上連續，且在 $(a,b)$ 上可導，則存在一個 $c\in (a,b)$ 使得 $f'(c)={\frac {f(b)-f(a)}{b-a}}$

它被稱為中值定理，因為從圖形上看，該定理指出，如果你有一個函式及其割線，那麼總會有一個函式上的切線與割線平行。

注意，它是應用於連線 $f(a)$ 和 $f(b)$ 的割線的羅爾定理的推廣形式。你可以在定理的等式中看到這一點，方法是讓 $f(a)=f(b)$ 。因為它非常相似，所以證明結構也驚人地相似。但是，由於使用割線段而不是可以輕鬆歸零的水平割線，因此將需要更多的代數運算。

證明

證明將問題簡化為可以使用羅爾定理解決的問題，透過某種意義上說，根據直線對圖形進行標準化，即所討論的函式是在直線的角度而不是笛卡爾網格的角度進行分析的。

中值定理的證明

我們根據函式 $f$ 和一個使用端點之間割線相同斜率的線性函式建立一個新函式 $(a,f(a))$ 和 $(b,f(b))$ 。 注意，該線性函式不是割線。 這個新函式，根據連續性和可導性定理，保持了函式 $f$ 給出的所有連續性和可導性。	$h=f-{\frac {f(b)-f(a)}{b-a}}(x-a)$
我們現在將檢查羅爾定理是否可以應用於這個新函式。	$x=a$	$x=b$
	$h(a)=f(a)$	${\begin{aligned}h(b)&=f(b)-f(b)+f(a)\\&=f(a)\end{aligned}}$
滿足羅爾定理條件，我們可以得出其結論，即 ${\textstyle \exists c:h'(c)=0}$，並由此繼續推導。	${\begin{aligned}h'(x)&=f'(x)-\left[{\dfrac {f(b)-f(a)}{b-a}}(x-a)\right]'\\&=f'(x)-{\dfrac {f(b)-f(a)}{b-a}}\\0&=f'(c)-{\dfrac {f(b)-f(a)}{b-a}}\\\end{aligned}}$
	$f'(c)={\dfrac {f(b)-f(a)}{b-a}}$
$\blacksquare$

柯西中值定理

這個定理是 中值定理 的一個更強的版本，它將中值定理中使用的割線擴充套件到其他型別的函式。

定理 如果 $f(x),g(x)$ 在 $[a,b]$ 上連續，在 $(a,b)$ 上可導（不包括兩個函式在同一點上都有無窮導數的情況），則存在 $c\in [a,b]$ 使得 ${\frac {f'(c)}{g'(c)}}={\frac {f(b)-f(a)}{g(b)-g(a)}}$

證明

定義函式 $h:[a,b]\to \mathbb {R}$ 為

$h(x)=f(x){\big (}g(b)-g(a){\big )}-g(x){\big (}f(b)-f(a){\big )}$

顯然，該函式滿足 $h(a)=h(b)$，根據羅爾定理，存在一個 $c\in [a,b]$ 使得 $h'(c)=0$。

關於變化的定理

在我們證明關於導數的更多內容之前，我們應該定義一些在以下證明中會用到的函式方面的概念。

“在區間 $A$ 上遞增的函式”的定義 給定一個函式 $f$ 和兩個數 $a,b\in A$ 使得 $a<b\ \Rightarrow \ f(a)<f(b)$

“在區間 $A$ 上遞減的函式”的定義 給定一個函式 $f$ 和兩個數 $a,b\in A$ 使得 $a<b\ \Rightarrow \ f(a)>f(b)$

如果沒有提及區間，則預設區間為實數。

有了這兩個定義，我們現在將探討我們從導數中學習到的一個簡單概念：變化。以下證明將從數學上嚴格地驗證這些概念，並提供新的工具來驗證函式的性質，並提供一些可以改進以證明新概念的工具。

“遞增函式具有正變化”定理

這個定理沒有正式名稱，它是驗證導數的簡單定義“衡量變化”的證明。它指出

定理 給定一個函式 $f$ ，使得對於某個區間 $A$ ，$f(x)>0$ ，那麼 $f$ 在區間 $A$ 上也是遞增的。

證明

這個證明依賴於斷言條件並使用一個定理（即均值定理）推匯出結論。

我們首先選擇任何兩個點 $a,b\in A$ ，使得 $a<b$ ，並假設整個區間內 $f'(x)>0$ 。

因為函式 $f$ 在 $A$ 上可微分，因此它在 $A$ 上也是連續的。因此，均值定理的所有條件都滿足，我們可以使用它。

$\exists x:f'(x)={\frac {f(b)-f(a)}{b-a}}>0$

經過一些代數運算，

${\begin{aligned}f'(x)={\dfrac {f(b)-f(a)}{b-a}}&>0\\f(b)-f(a)&>0\\f(b)&>f(a)\end{aligned}}$

提醒一下， $b-a>0$ 。

讓這個證明針對區間 A 中所有可能的 $a,b$ 組合進行迭代。所有 $a<b$ 都意味著 $f(a)<f(b)$ ，給定條件。

$\blacksquare$

推論

類似的證明適用於遞減函式。事實上，

定理 給定一個函式 $f$，使得對於某個區間 $A$，有 $f'(x)<0$，那麼 $f$ 在區間 $A$ 上也必須是遞減的。

證明與上一個證明映象對稱。

$\blacksquare$

"二階導數指示區域性最小值/最大值" 定理

這個定理沒有正式名稱，它證明了如何判斷找到的臨界點是區域性最小值還是區域性最大值。它指出

定理 給定一個函式 $f$，使得對於某個 $x$，有 $f'(x)=0$ 且 $f''(x)>0$，那麼 $f(x)$ 是一個區域性最小值。

證明

證明需要使用給定的條件來呼叫之前定理的證明，從而推斷出結果。

我們首先呼叫二階導數的定義 $f''(x)=\lim _{h\to 0}{\frac {f'(x+h)-f'(x)}{h}}>0$

從這裡，我們注意到 $f'(x)=0$，這意味著方程現在變為 $f''(x)=\lim _{h\to 0}{\dfrac {f'(x+h)}{h}}>0$

由於 $f''(x)>0$，這意味著不等式需要確保其正性，這意味著

$h\to 0^{+}$	$h\to 0^{-}$
$f(x+h)>0$	$f(x+h)<0$
因為為了讓 $f''(x)>0,f'(x+h)>0$ 成立，我們可以使用之前證明的結果來說明，因為 $f'(x+h)>0$ , $f$ 必須是遞增的。	因為為了讓 $f''(x)>0,f'(x+h)<0$ 成立，我們可以使用之前證明的結果來說明，因為 $f'(x+h)<0$ , $f$ 必須是遞減的。

由於連續函式在 $h$ 增加時，從遞減變為遞增，它必須在定義的區域性最小值處停止。

$\blacksquare$

推論

當推斷區域性最大值是否可以以相同的方式完成時，類似的證明也適用。事實上，

定理 給定一個函式 ƒ，使得 $f'(x)=0$ 且 $f''(x)<0$ 對於某個 x 成立。ƒ(x) 是一個區域性最大值。

證明與上一個證明映象對稱。

$\blacksquare$

泰勒定理

令 $f:[a,x]\to \mathbb {R}$

令 $f^{(n-1)}$ 在 $[a,x]$ 上可微

那麼，存在 $c\in (a,x)$ 使得

$f(x)=f(a)+{\frac {(x-a)f'(a)}{1!}}+{\frac {(x-a)^{2}}{2!}}f''(a)+\cdots +{\frac {(x-a)^{n-1}}{(n-1)!}}f^{(n-1)}(a)+{\frac {(x-a)^{n}}{n!}}f^{(n)}(c)$

證明

證明使用一種稱為“伸縮求和”的技術。

考慮函式 $\phi :[a,x]\to \mathbb {R}$，定義為：

$\phi (y)=f(y)+{\tfrac {(x-y)f'(y)}{1!}}+{\tfrac {(x-y)^{2}f''(y)}{2!}}+\ldots +{\tfrac {A(x-y)^{n}}{n!}}$，其中常數 $A\in \mathbb {R}$ 被選擇以滿足 $\phi (a)=\phi (x)$

根據羅爾定理，存在一個 $c\in (a,x)$ 使得 $\phi '(c)=0$

展開，我們有（在應用乘積法則時要小心！）：

$0=\phi '(c)$

$=f'(c)+\left[{\tfrac {(x-c)f''(c)}{1!}}-f'(c)\right]+\left[{\tfrac {(x-c)^{2}f'''(c)}{2!}}-{\tfrac {(x-c)f''(c)}{1!}}\right]+\ldots$

$+\left[{\tfrac {(x-c)^{n-1}f^{(n)}(c)}{(n-1)!}}-{\tfrac {(x-c)^{n-2}f^{(n-1)}}{(n-2)!}}\right]-{\tfrac {A(x-c)^{n-1}}{(n-1)!}}$

可以改寫為以下的伸縮求和

$\left[f'(c)-f'(c)\right]+\left[{\tfrac {(x-c)f''(c)}{1!}}-{\tfrac {(x-c)f''(c)}{1!}}\right]+\ldots +\left[{\tfrac {(x-c)^{n-1}f^{(n)}(c)}{(n-1)!}}-{\tfrac {A(x-c)^{n-1}}{(n-1)!}}\right]=0$

也就是說，${\frac {(x-c)^{n-1}f^{(n)}(c)}{(n-1)!}}={\frac {A(x-c)^{n-1}}{(n-1)!}}$，或者 $A=f^{(n)}(c)$

現在，我們可以很容易地看到 $\phi (x)=f(x)$ 以及 $\phi (a)=f(a)+{\tfrac {(x-a)f'(a)}{1!}}+{\tfrac {(x-a)^{2}f''(a)}{2!}}+\ldots +{\tfrac {(x-a)^{n-1}f^{(n-1)}(a)}{(n-1)!}}+{\tfrac {(x-a)^{n}f^{n}(c)}{n!}}$

但根據我們的選擇，$\phi (x)=\phi (a)$，因此我們得到

$f(x)=f(a)+{\tfrac {(x-a)f'(a)}{1!}}+{\tfrac {(x-a)^{2}f''(a)}{2!}}+\ldots +{\tfrac {(x-a)^{n-1}f^{(n-1)}(a)}{(n-1)!}}+{\tfrac {(x-a)^{n}f^{n}(c)}{n!}}$

證畢