實分析/連續性

←極限

實分析 連續性

總變差→

現在我們已經定義了函式的極限，我們現在可以定義函式連續的概念。連續性捕捉了函式“沒有突跳或振盪”的直觀影像。然而，在本頁中，我們將從這個基本的定義轉向更有條理的東西；一些嚴謹的東西。這不僅在實分析中很重要，在其他數學領域也同樣重要。

連續性標誌著對函式的一種新的分類，尤其是在本頁後面解釋的定理將被使用時尤為突出。但是，如果線性閱讀此華夏公益教科書，那麼需要注意的是，華夏公益教科書將描述具有比連續性更多屬性的函式。例如，初等數學中的函式，如多項式、三角函式以及指數和對數函式，包含比連續函式更多的性質。我們還將看到一些不連續函式的例子，以說明一些不符合條件的常見函式。

定義

I 上的連續函式定義

---

給定一個區間 $I$ 和一個函式 $f:I\to \mathbb {R}$，在I上連續被定義為維持以下性質

$\forall \varepsilon >0:\exists \delta >0:\forall x\in I:\exists c\in \mathbb {R} :|x-c|<\delta \implies |f(x)-f(c)|<\varepsilon$

它記為 $\lim _{x\to c}f(x)=f(c)$

讀者可能會注意到這個定義與 極限的定義 的相似之處，因為與極限不同，極限中函式 $f$ 可以收斂到任何值，而連續性限制返回值只能是函式 $f$ 被評估時的預期值。這種額外的限制提供了許多新定理，其中一些更重要的定理將在以下標題中顯示。

運算

由於極限在代數運算下是保持的，讓我們檢查一下連續性是否也一樣。

代數

我們看到，如果 $f(x)$ 和 $g(x)$ 都在 c 處連續，連續性對於以下情況仍然有效

在代數運算下保持連續性的函式列表

加法	$\lim _{x\rightarrow c}{(f+g)(x)}=f(c)+g(c)$
減法	$\lim _{x\rightarrow c}{(f-g)(x)}=f(c)-g(c)$
乘積	$\lim _{x\rightarrow c}{(f\cdot g)(x)}=f(c)\cdot g(c)$
函式的倍數	$\lim _{x\rightarrow c}{\lambda \cdot g(x)}=\lambda \cdot g(c)$
倒數	$\lim _{x\rightarrow c}{\left({\dfrac {1}{g}}\right)(x)}={\dfrac {1}{g(c)}}$
除法	$\lim _{x\rightarrow c}{\left({\dfrac {f}{g}}\right)(x)}={\dfrac {f(c)}{g(c)}}$

需要注意的是，對於任何除法，g(c) 必須是一個有效數字，即不為 0。

這實際上是極限代數運算的保持性的推論。只需將極限值 *L* 和 *M* 分別替換為 ƒ(c) 和 g(c) 即可。

我們可以使用順序極限來證明函式是不連續的，如下所示

• $f(x)$ 在 $c$ 處不連續當且僅當存在兩個序列 $(x_{n})\rightarrow c$ 和 $(y_{n})\rightarrow c$ 使得 $\lim _{n\rightarrow \infty }(f(x_{n}))\not =\lim _{n\rightarrow \infty }(f(y_{n}))$.

複合

複合函式要複雜得多，但它仍然像直覺所暗示的那樣起作用：兩個連續函式的複合仍然是連續函式。

定理

---

如果 $f:B\rightarrow \mathbb {R}$ 在 $g(x)$ 的值域上是連續的，並且 $g:A\rightarrow B$ 在任何區間 $A$ 上是連續的，那麼複合函式 $(f\circ g)(x)=f(g(x))$ 在 A 上是連續的。

證明過程很簡單，只需要滿足複合函式 $f$ 和 $g$ 的連續性定義，並基於滿足所有變數要求進行變數替換。因此，除了純粹的定義之外，沒有使用代數和定理。

證明覆合函式在點 c 處的連續性

首先，我們知道連續性需要滿足哪些條件。因此，我們將使用最基本的定義來定義 ε，它滿足連續性要求。	令 $\epsilon >0$
由於 f 必須是連續的，我們也寫下我們知道為真的一件事——它滿足連續性的屬性列表。現在，我們將對 δ 變數進行一個小的修改，原因將在後面說明。	$\exists \delta _{1}>0:|x-c|<\delta _{1}\implies |f(x)-f(c)|<\epsilon$.
然而，$f$ 還有更多屬性。關鍵在於 $c$ 和 $x$ 代表什麼。由於函式 $f$ 在 $g(x)$ 的取值範圍內是連續的，這意味著 $f$ 的輸入值實際上是 $g$ 的輸出值。因此，我們可以用 $g(x)$ 的輸出值來有效地替換函式 $f$ 中的 $c$ 和 $x$ 。	$\exists \delta _{1}>0:|g(x)-g(c)|<\delta _{1}\implies |f\circ g(x)-f\circ g(c)|<\epsilon$.
由於 g 必須是連續的，我們還會寫下我們知道是正確的，也就是連續性的定義。	$\exists \delta _{2}>0:|x-c|<\delta _{2}\implies |g(x)-g(c)|<\epsilon$.
表示式 $|g(x)-g(c)|<\epsilon$ 和 $|g(x)-g(c)|<\delta _{1}$ 非常相似。我們可以利用這個優勢，看看是否可以利用我們知道的任何屬性。鑑於 $\epsilon$ 的唯一要求是它必須為正數，並且它的不等式關係對任何數都成立，並且 $\delta _{1}$ 是正數，並且是數字，那麼我們可以把二者聯絡起來，將 $\epsilon$ 定義為 $\delta _{1}$。	令 $\epsilon =\delta _{1}$
因此，我們抽象地將連續性的定義串聯起來，建立在我們已知為真的基礎上；$f$ 和 $g$ 的連續性。閱讀此新的蘊涵語句所暗示的有效結果；$f$ 和 $g$ 複合函式的連續性，我們確信我們的斷言，即 $f$ 和 $g$ 的複合函式也是連續的。QED。	因此 $|x-c|<\delta _{2}\implies |g(x)-g(c)|<\delta _{1}\implies |f(g(x))-f(g(c))|<\epsilon$ 所以 $f\circ g(x)$ 在 A 上是連續的。
$\square$

三個連續性定理

想想連續性的直觀概念。如果你無法想象一個多項式函式的影像，它總是有效的。當它穿過函式域時，平滑曲線是連續性的圖形表示。但是，我們如何在數學上知道它是連續的呢？好吧，我們將從三個連續性定理開始，這些定理將驗證這種概念。

介值定理

這是關於連續性的一個重要定理。它本質上說連續函式沒有突然的跳躍或斷裂。

定理

---

令 f(x) 為一個連續函式。如果 $a<b$ 且 $f(a)<m<f(b)$，則 $\exists c\in (a,b):f(c)=m$.

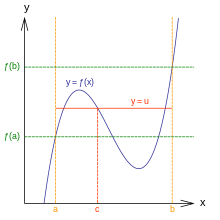介值定理：給定 [a,b] 上的連續函式和三個變數 a < c < b，則必須滿足 ƒ(a) < ƒ(c) < ƒ(b) 的條件。

證明

令 $S=\{x\in (a,b):f(x)<m\}$，並令 $c=\sup S$。

令 $\epsilon =|f(c)-m|$。根據連續性，$\exists \delta :|x-c|<\delta \implies |f(x)-f(c)|<\epsilon$。

如果 f(c) < m，那麼 $|f(c+{\frac {\delta }{2}})-f(c)|<\epsilon$，因此 $f(c+{\frac {\delta }{2}})<f(c)+\epsilon =m$。但是，$c+{\frac {\delta }{2}}\in S$，這意味著 c 不是 S 的上界，矛盾。

如果 f(c) > m，那麼由於 $c=\sup S$，$\exists x:x\in S,c>x>c-\delta$。但由於 $|x-c|<\delta$，$|f(x)-f(c)|<\epsilon$，因此 $f(x)>f(c)-\epsilon$ = m，這意味著 $x\notin S$，矛盾。 $\Box$

現在我們證明最小-最大定理，它是另一個與連續性相關的重大結果。實質上，它指出任何閉區間的連續像都是有界的，並且也取得這些界。

最小-最大定理

該定理作為另一個更大定理的第一部分。然而，它本身有助於彌合關於函式的上確界和下確界之間的差距。

定理

---

給定一個在 [a,b] 上的連續函式 ƒ，即 $f:[a,b]\to \mathbb {R}$，那麼 $f([a,b])$ 是有界的。

證明

假設$f$ 是無界的。

設$x_{1}={\tfrac {a+b}{2}}$。那麼，$f$ 在至少一個閉區間$[a,x_{1}]$ 和 $[x_{1},b]$ 上是無界的（否則，$f$ 在$[a,b]$ 上是有界的，與假設矛盾）。將這個區間稱為$I_{1}$。

類似地，將$I_{1}$ 分成兩個閉區間，並設$I_{2}$ 是$f$ 是無界的那個區間。

因此我們得到一個巢狀閉區間的序列$[a,b]\supseteq I_{1}\supseteq I_{2}\supseteq \ldots$，使得$f$ 在每個區間上都是無界的。

我們知道，巢狀閉區間的交集非空。因此，設$x_{0}\in I_{1}\cap I_{2}\cap \ldots$

由於 $f(x)$ 在 $x=x_{0}$ 處連續，所以存在一個 $\delta >0$ 使得 $x\in V_{\delta }(x_{0})\implies f(x)\in (f(x_{0})-1,f(x_{0})+1)$ 但根據定義，總存在一個 $k\in \mathbb {N}$ 使得 $I_{k}\subseteq V_{\delta }(x_{0})$，這與假設 $f$ 在 $I_{k}$ 上無界矛盾。因此，$f$ 在 $[a,b]$ 上有界。

極值定理

這是定理的第二部分。它是前一個定理更具肯定性的版本，指出不僅存在上確界和下確界，而且函式 ƒ 也能達到它們，並且它們將在你指定的區間內。

定理

---

給定一個在 [a,b] 上連續的函式 ƒ，即 $f:[a,b]\to \mathbb {R}$，如果 $M,m$ 分別是 $f([a,b])$ 的上界和下界，那麼存在 $c,d\in [a,b]$ 使得 $f(c)=M,f(d)=m$。

極值定理的圖示：給定一個在 [a,b] 上連續的函式，一定存在一個最大值 c 和一個最小值 d，使得 ƒ(c) 是區間內的最大值，而 ƒ(d) 是區間內的最小值。

證明

假設如果可能，$M=\sup(f([a,b]))$，但 $M\notin f([a,b])$。

考慮函式 $g(x)={\frac {1}{M-f(x)}}$。根據連續性的代數性質，$g:[a,b]\to \mathbb {R}$ 是連續的。然而，$M$ 是 $f([a,b])$ 的聚點，$g(x)$ 在 $[a,b$ 上無界，與 (i) 矛盾。因此，$M\in f([a,b])$。類似地，我們可以證明 $m\in f([a,b])$。

附錄

連續性將在數學的其他分支中再次出現。你不僅會遇到連續性的不同變體，還會遇到連續性的不同定義。

一致連續性

令 $A\subseteq \mathbb {R}$
令 $f:A\to \mathbb {R}$

我們說 $f$ 在 $A$ 上是一致連續的當且僅當對於每一個 $\varepsilon >0$ 都存在 $\delta >0$，使得如果 $x,y\in A$ 且 $|x-y|<\delta$，那麼 $|f(x)-f(y)|<\varepsilon$

利普希茨連續性

令 $A\subseteq \mathbb {R}$
令 $f:A\to \mathbb {R}$

我們說 $f$ 在 $A$ 上是利普希茨連續的當且僅當存在一個正實常數 $K$ 使得，對所有 $x,y\in A$，$|f(x)-f(y)|\leq K|x-y|$.

最小的這樣的 $K$ 被稱為函式 $f$ 的利普希茨常數。

拓撲連續性

如前所述，連續函式的概念在數學的幾個領域都有使用，最顯著的是在拓撲學中。在這樣的場景中，連續性的另一種表徵非常有用。

定理

令 $A\subseteq \mathbb {R}$
令 $f:A\to \mathbb {R}$

$f(x)$ 在 $x=c$ 處連續當且僅當對於 $f(x)$ 的每個開鄰域 $V$，都存在 $x$ 的一個開鄰域 $U$，使得 $U\subseteq f^{-1}(V)$

需要指出的是，“開集”的概念可以被定義在比實數集或度量空間更一般的環境中，因此這種描述方法具有很高的實用性。