材料強度/應力狀態

工程力學中的材料強度

(最後) →

主應力

一般的應力狀態可以用一個對稱的 3 x 3 矩陣來表示。

總是可以找到一個座標系，使得所有的剪下應力都為零。然後，3 x 3 矩陣被對角化，對角線上是三個主應力，所有其他分量都等於零。三個主應力通常標記為σ₁、σ₂和σ₃。
σ₁ 是最大的 (拉伸最大的) 主應力，σ₃ 是最小的 (壓縮最大的) 主應力，σ₂ 是中間的主應力。

應力不變數

$I_{1}=\sigma _{3}+\sigma _{2}+\sigma _{1}$

$I_{2}=\sigma _{1}\sigma _{2}+\sigma _{2}\sigma _{3}+\sigma _{3}\sigma _{1}$

$I_{3}=\sigma _{1}\sigma _{2}\sigma _{3}$

靜水應力

所謂的靜水應力 σ_h 由下式給出

$\sigma _{h}=\left.{\frac {\sigma _{1}+\sigma _{2}+\sigma _{3}}{3}}\right.$

偏應力

正應力 - 壓力

where pressure = average stress

莫爾圓

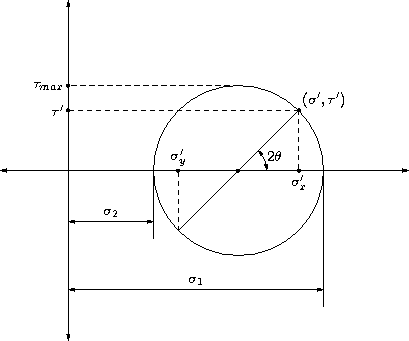
考慮二維應力狀態，其中應力為σ_x、σ_y和τ_xy。我們有，對於另一個與x-y 成θ角的正交軸系 x'-y' ，應力為

$\sigma _{x'}={\frac {\sigma _{x}+\sigma _{y}}{2}}+{\frac {\sigma _{x}-\sigma _{y}}{2}}\cos 2\theta +\tau \sin 2\theta$

$\tau _{x'y'}=-{\frac {\sigma _{x}-\sigma _{y}}{2}}\sin 2\theta +\tau _{xy}\cos 2\theta$

從上面的公式可以看出，對於由σ_x、σ_y和τ_xy 給定的任何應力狀態，我們都可以找到一個θ值，使得σ_x'的值最大。這個值稱為主應力σ₁（對於最大值）或σ₂（對於最小值）。

主應力由下式給出

$\sigma _{1,2}={\frac {\sigma _{x}+\sigma _{y}}{2}}\pm {\sqrt {\left({\frac {\sigma _{x}-\sigma _{y}}{2}}\right)^{2}+\tau _{xy}^{2}}}$

最大剪下應力由下式給出：

τ_max = (σ₁ − σ₂)/2

根據σ_x'和τ_x'y'的定義，我們有：

$\left(\sigma _{x'}-{\frac {\sigma _{x}+\sigma _{y}}{2}}\right)^{2}+\tau _{x'y'}^{2}=\left({\frac {\sigma _{x}-\sigma _{y}}{2}}\right)^{2}+\tau _{xy}^{2}$

在σ-τ圖中，這是一個圓，圓心位於x軸上，圓心到原點的距離由(σ_x + σ_y)/2給出，半徑由下式給出：

$R={\sqrt {\left({\frac {\sigma _{x}-\sigma _{y}}{2}}\right)^{2}+\tau _{xy}^{2}}}$

該圓被稱為莫爾圓，它有助於視覺化一點處的應力狀態。

上圖顯示了應力狀態(σ, τ)的莫爾圓。圓心和半徑由上述公式給出。另一個應力σ_y可以透過與(σ, τ)點相對的點讀出。任何平面上的應力可以透過簡單的幾何結構找到。

常見情況下的莫爾圓

在這種情況下，上述剪下應力為σ₁/2。

液體，根據定義，不能承受剪下力。因此，莫爾圓圖只是一個點。（這個點應該位於軸的負側，因為液體只能抵抗壓縮）

對於純剪下，莫爾圓的圓心位於原點。

失效準則

對於各向同性材料，物體上任意一點的應力狀態完全由主應力三元組確定。

現在我們能夠變換應力得到主應力，我們可以使用這些應力來考慮一些假設用於在雙軸和三軸應力狀態下材料失效的準則（理論），這些準則通常基於在單軸應力狀態下材料屈服和斷裂的實驗。根據這些實驗，失效型別取決於材料型別。延性材料（大多數金屬）的失效發生在達到彈性極限並開始屈服時。非延性材料（例如鑄鐵、混凝土）的失效發生在脆性斷裂。

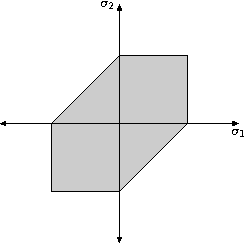
最大剪下應力準則

對於延性材料，一種失效理論是最大剪下應力理論。我們知道最大剪下應力由τ_max = (σ₁ − σ₂)/2給出。屈服強度σ_y可以透過單軸拉伸試驗確定。因此，如果最大剪下應力理論有效，則當最大剪下應力達到σ_y/2時發生失效。

在上圖中，如果應力狀態位於陰影區域之外，則材料會失效。

最大畸變能準則

如果最大剪下應力理論有效，則當最大剪下應力達到 ${\frac {{\sqrt {2}}\sigma _{y}}{3}}$ 時發生失效。

材料失效

每種材料的實際失效模式都是唯一的，儘管可以將某些準則應用於材料類別。 失效模式。疲勞失效，