材料力學/入門概念

工程力學中的材料力學

應力

應力被定義為平均力除以力作用的物體面積。更準確地說，我們可以談論一點的應力，或者簡稱為應力，這是當面積（一個無限小面積dA）接近於零時的極限情況。由於作用在無限小面積上的無限小力的法向分量而產生法嚮應力，而由於作用在無限小面積上的無限小力的切向分量而產生剪下應力。（注意：嚴格地說，應力並不存在。伸長率（ $\epsilon$ ) 和剛度 (E) 才存在。應力是一種方便的數學結構，它允許輕鬆地操作公式。）

考慮一個作用在任何任意角度上的微元面積 dA 上的力 dF。τ_xx = dF_x/dA 是法嚮應力，也表示為σ_x。剪下應力由τ_xy = dF_y/dA 和τ_xz = dF_z/dA 給出，其中 dF_y 和 dF_z 分別是力 dF 的 y 和 z 分量。這些剪下應力在平面y-z 上。

現在，不是考慮無限小的面積，而是考慮所討論點處的無限小的體積。設這個體積是一個以dx、dy 和dz 為邊的平行六面體。在這種情況下，一般來說有九個非零應力。它們形成一個應力張量，用以下 3x3 矩陣表示。

$\left({\begin{matrix}\sigma _{x}&\tau _{xy}&\tau _{xz}\\\tau _{yx}&\sigma _{y}&\tau _{yz}\\\tau _{zx}&\tau _{zy}&\sigma _{z}\end{matrix}}\right)$

因此，在平面應力情況下（例如，取平面x-y），我們將有四個分量的應力張量。此外，鑑於剪下應力對稱性（τ_xy = τ_yx = τ），上述 3x3 矩陣簡化為表示對稱平面應力張量的 2x2 對稱矩陣。

$\left({\begin{matrix}\sigma _{x}&\tau \\\tau &\sigma _{y}\end{matrix}}\right)$

剪下應力對稱性在三維情況下成立。這使得上述 3x3 矩陣（以及相應的應力張量）是對稱的：它的六個剪下應力分量中只有三個是獨立的。因此，應力張量通常有六個不同的分量：三個法嚮應力和三個剪下應力。如上所述，在二維情況下，應力張量只有三個不同的分量：兩個法嚮應力和一個剪下應力。

假設物體處於平衡狀態，並分別在x 和y 方向受到f_x 和f_y（每單位體積）的力作用。那麼可以證明，應力平衡方程在笛卡爾座標系中的形式為

${\frac {\partial \sigma _{x}}{\partial x}}+{\frac {\partial \tau }{\partial y}}=f_{x}$

${\frac {\partial \tau }{\partial x}}+{\frac {\partial \sigma _{y}}{\partial y}}=f_{y}$

因此，在平面應力情況下，我們有兩個方程涉及三個未知數。

現在轉向一個最簡單的物體一維載荷的例子。考慮一根兩端沿縱軸拉伸的杆。

如果我們取一個垂直於軸線的截面，很容易看出σ_x = P/A，其中P 是載荷，A 是截面的橫截面積。

現在考慮橫截面相對於縱軸傾斜θ 的情況。在這種情況下，我們可以將力P 分解到沿截面和垂直於截面的方向。力的分量分別為P cosθ 和P sinθ。橫截面的面積現在為A / cosθ。法嚮應力為σ_θ = P cosθ/(A/ cosθ) = (P/A) cos²θ。類似地，剪下應力為τ_θ = (P/A) sinθ cosθ。

應變

材料的應變定義為尺寸變化量與原始尺寸之比，是一個無量綱量。它用符號 ε 表示，其中 ε = (L − L₀)/L₀。這裡 L₀ 稱為標距長度。

上述定義的應變稱為工程應變或名義應變，不同於自然應變或真應變，其定義為

$\epsilon _{n}=\int _{L_{0}}^{L}{\frac {dL'}{L'}}=\ln \left({\frac {L}{L_{0}}}\right)=\ln(1+\epsilon )$

請注意，對於較小的 ε 值，工程應變和自然應變是相同的，而且就本書中所述的大多數載荷和位移而言，其差異並不重要。此外，使用符號 e 表示工程應變和符號 ε 表示真應變的做法並不罕見。

在無窮小的情況下，我們有應變 ε_x = du/dx，其中 du 是線段 dx 的長度變化。因此，總長度變化由 Δ = ∫₀^L du = ∫₀^L ε_x dx 給出。

胡克定律

胡克定律指出，對於某些材料，應力與應變呈線性關係。這是羅伯特·胡克發現的經驗定律，他在彈簧上觀察到這種行為。因此，對於一維情況，我們有：

$\sigma =E\epsilon$

其中 E 是稱為楊氏模量的比例常數。請注意，我們認為 E 的值在所有方向上都是相同的。其性質在各個方向上沒有方向變化的材料稱為各向同性材料。在不同方向上具有不同性質的材料稱為各向異性。各向異性的最常見原因是材料的晶體性質。但是，大多數常見的結構材料在較大範圍內沒有相同的晶體取向。各向異性的另一個原因是材料加工的方式。一些加工方式，例如拉拔，往往會在特定方向上產生應力。

將胡克定律應用於長度變化的定義，我們有：

$\Delta =\int _{0}^{L}{\frac {\sigma }{E}}dx=\int _{0}^{L}{\frac {P}{AE}}dx$

或者：

$\Delta ={\frac {PL}{AE}}$

從力學中我們知道，彈簧的伸長量與力呈線性關係，比例常數通常用 k 表示。因此，軸向載荷作用下樑的彈簧常數為 AE/L。這可以擴充套件到不同形狀的部件，因此結構是按複雜方式排列的彈簧的組合體。

泊松比

在許多材料中，縱向應變與橫向應變呈線性關係。橫向應變與縱向應變之比稱為泊松比，用 ν 表示。

$\nu =-{\frac {\epsilon _{lat}}{\epsilon _{long}}}$

泊松比的值因材料而異，大多數常見金屬約為 0.30。

近年來，再入材料的發現引起了極大的興趣。這些是具有負泊松比的獨特蜂窩和泡沫。三維各向同性固體中泊松比的允許範圍為 -1 到 1/2（儘管一些聚合物泡沫已被發現表現出 1.0 的值）。

溫度影響

材料由於溫度變化而改變長度。為了量化該值，長度和溫度必須參考某個確定的溫度。變化率由線性熱膨脹係數量化，用變數 CoF & α 表示，根據應變定義，我們有 ε = α ΔT，其中 ΔT 是溫度變化（與給定參考點相比）。如果我們在剛性支撐之間有一個結構構件，則該構件內會產生 ΔT 的應變。還存在相關的應力，稱為熱應力，但是對於由於溫度變化而改變長度但不受約束的構件，不會產生應力。橫截面由不同 CoF 的材料組成的結構構件，會帶來一個更復雜的問題。

由於變形而儲存的能量

當壓縮一根杆時，對杆所做的功將以能量的形式儲存起來。在上圖中，儲存的能量顯示為陰影區域。現在，我們知道，對於彈簧常數為 k、伸長量為 x 的彈簧，其儲存的能量為 1/2 k x²。對於一根杆，其常數為 AE/L、伸長量為 PL/AE，其儲存的能量為 1/2 P²L / AE。從上述公式可以看出，對於相同的直徑和材料，使用長螺栓比短螺栓好，因為長螺栓的峰值載荷 P 更低，而無需進行任何動力學分析。

彈性變形和塑性變形

到目前為止，我們已經考慮了在施載入荷時發生彈性變形的構件。其中一些符合胡克定律，因此應力與應變之間的關係是線性的。彈性變形是指材料在外部載荷去除後能夠恢復其原始形狀的能力。但是，我們知道，對於較大的載荷，材料的變形是永久性的，這稱為塑性變形。能夠進行塑性變形的金屬稱為延性材料。無法進行塑性變形的材料稱為脆性材料。

彈性區域非常小的材料稱為塑性材料。上圖顯示了這種材料的理想化。當達到一定的應力狀態時，材料會流動。

能夠承受較大變形並保持彈性的材料被稱為彈性材料。上圖顯示了一種理想的彈性材料——在這種情況下，它也遵循胡克定律，被稱為線性彈性材料。需要注意的是，一種物質可以是彈性的，但仍然不遵循胡克定律（非線性彈性）。

大多數金屬在小載荷下會發生彈性變形，在更大載荷下會發生塑性變形。對於大多數金屬來說，當材料發生塑性變形時，應力會有一定的增加。然而，上面所示的彈塑性近似對於簡單的分析來說已經足夠了。

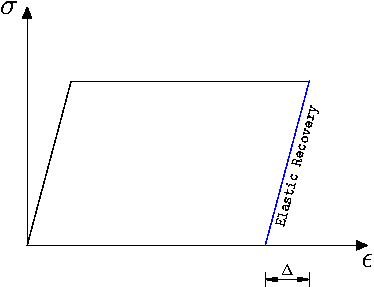
需要注意的是，表現出這種行為的材料會顯示出所謂的彈性恢復，即樣品會表現出一定的恢復到之前狀態的趨勢。在上圖中，在載荷移除後，恢復量為Δ。注意，在解除安裝狀態下，材料存在殘餘變形。

有些材料在塑性流動過程中表現出應力增加，這種現象被稱為應變硬化。在這種情況下，可以使用具有兩個斜率的應力應變曲線來近似模擬它們，但這種分析在實際應用中很少使用，因為大多數結構變形發生在彈性區域，塑性流動很可能被認為是失效模式。

剪下應變和模量

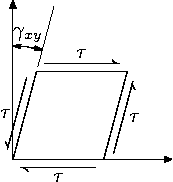
之前我們介紹了材料在軸向載荷作用下的應力-應變關係，我們發現應力σ與應變ε成正比。如果我們將剪下應力τ與剪下應變γ作圖，對於遵循胡克定律的材料，我們將得到一條直線。因此，胡克定律可以使用以下方程擴充套件到剪下應力：τ = Gγ，其中G是剪下模量，γ是剪下應變。