波動/費馬原理

波動 : 幾何光學
1 - 2 - 3 - 4 - 5 - 6
問題

費馬原理

費馬原理可以用來發展幾何光學的一種替代方法。該原理（以最簡單的形式）指出，給定頻率的光波在兩點之間傳播的路徑需要最短的時間。最明顯的例子是光穿過均勻介質，其中光速不會隨位置變化。在這種情況下，最短時間等效於兩點之間的最短距離，眾所周知，這條線是一條直線。因此，費馬原理與光在均勻介質中沿直線傳播是一致的。

費馬原理也可以用來推匯出反射和折射定律。例如，圖 3.10 顯示了反射光線的候選光線，其中入射角和反射角不相等。光從 A 點傳播到 B 點所需的時間為

t=[\{h_{1}^{2}+y^{2}\}^{1/2}+\{h_{2}^{2}+(w-y)^{2}\}^{1/2}]/c

(4.12)

其中 $c$ 是光速。我們透過對 $t$ 關於 $y$ 進行微分，並將結果設為零，得到

{\frac {y}{\{h_{1}^{2}+y^{2}\}^{1/2}}}={\frac {w-y}{\{h_{2}^{2}+(w-y)^{2}\}^{1/2}}}.

(4.13)

然而，我們注意到這個等式的左側僅僅是 $\sin \theta _{I}$ ，而右側是 $\sin \theta _{R}$ ，因此最小時間條件簡化為 $\sin \theta _{I}=\sin \theta _{R}$ 或 $\theta _{I}=\theta _{R}$ ，這就是反射定律。

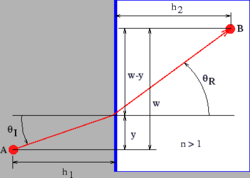
類似的分析可以用來推匯出斯涅爾折射定律。光在折射率為 $n$ 的介質中的速度為 $c/n$ ，其中 $c$ 是其在真空中的速度。因此，光在該介質中傳播一定距離所需的時間是 $n$ 倍於光在真空中傳播相同距離所需的時間。參考圖3.11，光從A到B所需的時間變為

t=[\{h_{1}^{2}+y^{2}\}^{1/2}+n\{h_{2}^{2}+(w-y)^{2}\}^{1/2}]/c.

(4.14)

這導致了以下條件：

\sin \theta _{I}=n\sin \theta _{R}

(4.15)

其中 $\theta _{R}$ 現在是折射角。我們識別出這個結果是斯涅爾定律。

請注意，反射案例說明了關於費馬原理的一點：最小時間實際上可能是區域性最小值而不是全域性最小值——畢竟，在圖3.10中，從A到B的全域性最小距離仍然只是兩點之間的直線！實際上，從點A開始的光將透過兩條路徑到達點B——直線路徑和反射路徑。

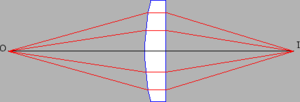
圖3.13說明了一種相當奇特的情況。請注意，從點O發出並與透鏡相交的所有光線最終都落在了點I上。這似乎與費馬原理相矛盾，因為只有最小（或最大）時間軌跡應該出現。然而，計算表明，在這個特定情況下，所有說明的軌跡都花費了相同的時間。因此，光不能使用費馬原理選擇一條軌跡而不是另一條，所有軌跡都同樣有利。請注意，這個推論並不適用於任何軌跡集合，而只適用於從一個焦點到另一個焦點的軌跡集合。

波動 : 幾何光學
1 - 2 - 3 - 4 - 5 - 6
問題