 模函式
模函式模函式寫作  ,它的定義為
,它的定義為  。你也可以寫作
。你也可以寫作  ,因為二次冪會將任何負數變為正數,然後你取開方,函式變回原來的函式。模函式具有多對一對映,因此沒有反函式。當結果的值而不是它的符號很重要時,就會使用模函式。在英國英語中,模函式這個詞通常用來表示它,否則它被稱為 *絕對值函式*。所以在大多數計算器上你會看到 abs()。
,因為二次冪會將任何負數變為正數,然後你取開方,函式變回原來的函式。模函式具有多對一對映,因此沒有反函式。當結果的值而不是它的符號很重要時,就會使用模函式。在英國英語中,模函式這個詞通常用來表示它,否則它被稱為 *絕對值函式*。所以在大多數計算器上你會看到 abs()。
當解包含模的不等式時,重要的是記住你不能簡單地忽略模。相反,你需要使用規則:  。然後你像解普通問題一樣解它。例如
。然後你像解普通問題一樣解它。例如
解關於 x 的方程 



在  的影像中,影像的負半部分被反射到 x 軸上。以下是
的影像中,影像的負半部分被反射到 x 軸上。以下是  的影像。
的影像。

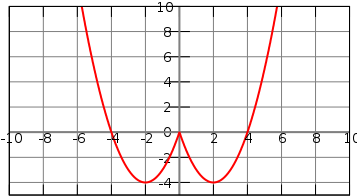
在  的影像中,影像的正半部分被反射到 y 軸上。以下是
的影像中,影像的正半部分被反射到 y 軸上。以下是  的影像。
的影像。

底數為 e 的函式是一個超越函式,由無窮級數定義,近似值為 2.71828
 .
.
e 是數學中最重要的數字之一,因為它被用於大多數自然增長過程的計算。由於它是一個指數函式,它遵循指數函式的所有定律。自然指數是自然對數的逆函式,因此  。右側是
。右側是  的影像。
的影像。
自然對數是底數為 e 的對數函式: 。它有一個特殊的符號
。它有一個特殊的符號  。由於自然對數是對數函式,它遵循對數函式的所有定律。自然對數是自然指數的逆函式,因此
。由於自然對數是對數函式,它遵循對數函式的所有定律。自然對數是自然指數的逆函式,因此  。右側是
。右側是  的影像。
的影像。
自然函式的主要用途之一是計算自然增長或衰減,可以使用以下公式計算: ,其中 y(t) 是最終值,
,其中 y(t) 是最終值, 是初始值,k 是增長常數,t 是經過的時間。有一種特殊的衰減是元素的半衰期,其中 k 定義為:
是初始值,k 是增長常數,t 是經過的時間。有一種特殊的衰減是元素的半衰期,其中 k 定義為: 。指數增長和衰減在從測量細菌菌落生長到計算涉及利息的方面都有非常廣泛的應用。
。指數增長和衰減在從測量細菌菌落生長到計算涉及利息的方面都有非常廣泛的應用。
一個細菌菌落從 200 個細菌開始,在 2 小時內菌落增長到 600 個細菌。預測 6 小時後菌落中細菌的數量?
由此我們知道
- y(t) = 600
 = 200
= 200- k = x
- t = 2
現在我們將值代入公式

現在我們確保 e 是單獨的

由於 ln 是反函式,我們使用它來移除底數 e。

現在我們可以解 x。
 ,所以菌落的增長因子大約為 .55
,所以菌落的增長因子大約為 .55
現在我們可以預測 6 小時後細菌的數量。


碳-14 的半衰期為 5730 年。100 克 C-14 樣本什麼時候會減少到 20% C-14 和 80% C-12?
- y(t) = 20% * 100 = 20
 = 100
= 100- half-life = 5730
- t = x
我們將所有已知值代入函式。注意增長常數的特殊公式。

現在我們確保 e 是單獨的

由於 ln 是反函式,我們使用它來移除底數 e。


現在我們將方程重新排列以隔離 t。

解 t 我們得到樣本將在大約 13304.6 年後減少到 20% C-14 和 80% C-12。

在核心3中,我們用另外三個反射來完成我們的變換表。以下是變換的完整表格。
 是
是  關於x軸的反射。
關於x軸的反射。 是
是  關於y軸的反射。
關於y軸的反射。 是
是  當 y < 0 時,關於x軸的反射。
當 y < 0 時,關於x軸的反射。 是
是  當 x > 0 時,關於y軸的反射。
當 x > 0 時,關於y軸的反射。 是
是  關於直線 y=x 的反射。
關於直線 y=x 的反射。  必須具有 1:1 對映。
必須具有 1:1 對映。
 如果
如果  ,則它會遠離y軸拉伸;如果
,則它會遠離y軸拉伸;如果  ,則它會靠近y軸拉伸。在這兩種情況下,變化都是 1/b 個單位。
,則它會靠近y軸拉伸。在這兩種情況下,變化都是 1/b 個單位。 如果
如果  ,則向 x 軸方向拉伸;如果
,則向 x 軸方向拉伸;如果  ,則遠離 x 軸方向拉伸。在這兩種情況下,變化量都是 a 個單位。
,則遠離 x 軸方向拉伸。在這兩種情況下,變化量都是 a 個單位。
 是 f(x) 向右平移 h 個單位。
是 f(x) 向右平移 h 個單位。 是 f(x) 向左平移 h 個單位。
是 f(x) 向左平移 h 個單位。 是 f(x) 向上平移 k 個單位。
是 f(x) 向上平移 k 個單位。 是 f(x) 向下平移 k 個單位。
是 f(x) 向下平移 k 個單位。
描述函式  如何對映到
如何對映到  。
。
1) 關於 x 軸對稱。
2) 在 x 方向拉伸 4 倍。
3) 在 x 方向平移 5 個單位到左側,或者說關於直線 x = -5 對稱。
4) 在 y 方向平移 10 個單位到上方。
5) 關於直線 y = x 對稱。
6) 當 y < 0 時,關於 x 軸對稱。
7) 當 x > 0 時,關於 y 軸對稱。
現在來看圖形
 透過這些變換,很難認出這是
透過這些變換,很難認出這是  的圖形。
的圖形。























































