以下是處理對映問題時使用的符號。
 表示一組...。
表示一組...。
例如, 表示一組
表示一組 ,其中
,其中 大於或等於 2。
大於或等於 2。
 表示函式 f 將集合 X 對映到集合 Y。另一種寫法是
表示函式 f 將集合 X 對映到集合 Y。另一種寫法是  。
。
 - 自然數 - 例如,{1,2,3,. ..}
- 自然數 - 例如,{1,2,3,. ..}
 - 整數 - 例如,{...−2,−1,0,1,2,. ..}
- 整數 - 例如,{...−2,−1,0,1,2,. ..}
 - 分數(有理數)
- 分數(有理數)
 - 實數,包括有理數和無理數,但不包括複數,例如
- 實數,包括有理數和無理數,但不包括複數,例如 
無理數沒有通用符號 - 它們的符號是特定的 - 例如,{ }
}
對映:連線兩組專案的規則。
物件/輸入:起始集合中的一個專案。
映像/輸出:結束集合中的一個專案。
定義域:所有物件組成的集合。
陪域:所有可能的結束值組成的集合。
值域:陪域中實際使用的元素。
1) 唯一的 
 唯一的
唯一的  (1:1 或單射對映)
(1:1 或單射對映)
2) 若干個 
 唯一
唯一  (多對一對映)
(多對一對映)
3) 唯一 
 若干個
若干個  (一對多對映)
(一對多對映)
4) 若干個 
 若干個
若干個  (多對多對映)
(多對多對映)
注意:函式只能是一對一 (單射) 或多對一對映。
函式將每個輸入值對應到唯一的輸出值。如果存在兩個輸出值,則該公式就不是函式。例如  是函式,因為每個 x 只有一個輸出值,但
是函式,因為每個 x 只有一個輸出值,但  不是函式,因為每個 x 可能有兩個值,例如 4 =
不是函式,因為每個 x 可能有兩個值,例如 4 =  和
和  ,因此 x 可以是 2 或 -2。圓形(和類似形狀)的圖形代表多對多對映,因此它們不是函式。可以使用垂直線測試來確定圖形是否為函式。該測試指出,當且僅當繪製的任何垂直線與圖形只相交一次時,該圖形才為函式。函式共有四種表示方法:
,因此 x 可以是 2 或 -2。圓形(和類似形狀)的圖形代表多對多對映,因此它們不是函式。可以使用垂直線測試來確定圖形是否為函式。該測試指出,當且僅當繪製的任何垂直線與圖形只相交一次時,該圖形才為函式。函式共有四種表示方法:
1) 公式
2) 圖形
3) 表格
4) 文字描述
每個函式都有定義域和值域。定義域是輸入值的集合。值域是輸出值的集合。請記住,如果函式存在反射或平移,則定義域和值域中的一個或兩個都會存在反射或平移。例如
函式  的定義域是
的定義域是  ,值域是
,值域是  ,而函式
,而函式  的定義域是
的定義域是  ,值域是
,值域是  。參見 反射規則 1 和平移規則 2.
。參見 反射規則 1 和平移規則 2.
函式的定義域通常是所有  ,但以下三種情況除外:1) 如果 x 出現在分母中,分母為零的點不在定義域中,例如
,但以下三種情況除外:1) 如果 x 出現在分母中,分母為零的點不在定義域中,例如
 的定義域是除 1 之外的所有
的定義域是除 1 之外的所有  。
。
2) 如果指數小於零且為偶數,定義域將是  ,例如
,例如
 的定義域是
的定義域是  ,但
,但 ![{\displaystyle {\sqrt[{3}]{x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a55f866116e7a86823816615dd98fcccde75473) 的定義域是所有
的定義域是所有  。
。
3) 在分段函式中,定義域會受定義的限制,例如

 的定義域將是 (5,10)。
的定義域將是 (5,10)。
對於值域,有一個簡單的規則需要記住。所有偶函式的值域都是  ,奇函式的值域是所有
,奇函式的值域是所有  。
。
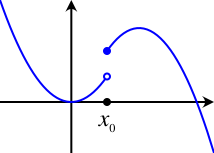
分段函式是在不同區間上由不同表示式給出的函式。  的圖形如右圖所示。空心圓表示該點未包含在圖形中,實心圓表示該點包含在圖形中。因此
的圖形如右圖所示。空心圓表示該點未包含在圖形中,實心圓表示該點包含在圖形中。因此  = 8,而不是 4。
= 8,而不是 4。
一對一函式必須對每個輸入都有唯一的輸出。例如, 不是一對一的,因為輸入 -2 和 2 都會產生輸出 4,但是
不是一對一的,因為輸入 -2 和 2 都會產生輸出 4,但是  是一對一的,因為每個輸入都會產生唯一的輸出,f(-2)= -8 且 f(2)=8。可以使用水平線測試來確定圖形是否是一對一的。該測試指出,當且僅當繪製的任何水平線與圖形僅相交一次時,函式才是一對一的。
是一對一的,因為每個輸入都會產生唯一的輸出,f(-2)= -8 且 f(2)=8。可以使用水平線測試來確定圖形是否是一對一的。該測試指出,當且僅當繪製的任何水平線與圖形僅相交一次時,函式才是一對一的。
函式的反函式將為函式的輸出值產生輸入值。函式必須是一對一的,反函式才存在。為了在數學上說明這一點: 和
和  。此外,反函式和函式的複合將產生 x:
。此外,反函式和函式的複合將產生 x: 。下面可以找到一個涉及蘋果和檸檬的示例。原始函式將蘋果變成檸檬,而反函式將檸檬變成蘋果。
。下面可以找到一個涉及蘋果和檸檬的示例。原始函式將蘋果變成檸檬,而反函式將檸檬變成蘋果。
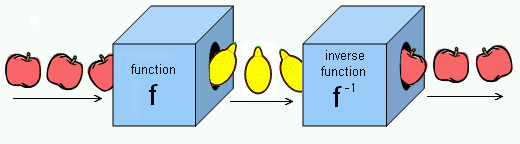
如何找到函式的反函式。
1) 求解關於 x 的方程
2) 將 y 與 x 交換。
3) 用  表示法寫出。
表示法寫出。
在例子中求  的反函式。
的反函式。
1) 

2) 
3) 
現在可以檢驗一下:  以及
以及  。
。
當我們畫一個一一函式的反函式的圖時,我們只需要交換x和y座標: (x,y) 變為 (y,x)。座標 (5,7) 在反函式的圖上將是 (7,5)。這個圖將是關於直線 y=x 的對稱圖形。在右側的例子中,紅色直線是  的圖,綠色直線是
的圖,綠色直線是 ![{\displaystyle f^{-1}\left(x\right)={\sqrt[{3}]{x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b50805e63e9e51c5d9161ee0d65bb2fb9bc14474) 的圖。
的圖。
函式合成的數學符號是  。或者,合成也可以寫成
。或者,合成也可以寫成 ![{\displaystyle f\left[g\left(x\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/48a7bc35b3f3b9700500700bfdd793b4bd01017c) 。當您合成兩個函式時,您用第二個函式替換變數的所有例項。您可以透過合成中函式的書寫順序來判斷函式的順序
。當您合成兩個函式時,您用第二個函式替換變數的所有例項。您可以透過合成中函式的書寫順序來判斷函式的順序  ,表示 F 由 G 組成。如果原始函式的定義域或值域以某種方式受限,那麼複合函式也會以相同的方式受限。例如,
,表示 F 由 G 組成。如果原始函式的定義域或值域以某種方式受限,那麼複合函式也會以相同的方式受限。例如, 和
和  ,求
,求  。然後找出定義域和值域。
。然後找出定義域和值域。
1) 將 f 中所有 x 的例項替換為  ,得到
,得到  。
。
2) 現在簡化。  。
。
3) 定義域將是  ,因為 g(x) 永遠不可能有負的 x 值,值域將是
,因為 g(x) 永遠不可能有負的 x 值,值域將是  ,因為 g(x) 永遠不可能為負。
,因為 g(x) 永遠不可能為負。



























![{\displaystyle {\sqrt[{3}]{x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a55f866116e7a86823816615dd98fcccde75473)


















![{\displaystyle f^{-1}\left(x\right)={\sqrt[{3}]{x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b50805e63e9e51c5d9161ee0d65bb2fb9bc14474)

![{\displaystyle f\left[g\left(x\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/48a7bc35b3f3b9700500700bfdd793b4bd01017c)








