座標是描述位置的一種方式。 在二維中,位置由兩個垂直方向給出,即 *x* 和 *y*。
直線具有固定的斜率。 直線的斜率及其 y 軸截距是區分一條直線與另一條直線的兩個資訊。
直線最常見的形式是 y = mx + c。 m 是直線的斜率,c 是直線與 y 軸的交點。 當 c 為 0 時,直線透過原點 (0,0)。 方程的其他形式為 x = a,用於無限斜率的垂直線,y = b 用於斜率為零的水平線。 此外,一些方程通常寫為:px + qy + c = 0。 您也可以使用方程 y-y1=m(x-x1)
直線的陡峭程度可以透過其斜率來衡量,斜率是 y 方向的變化量除以 x 方向的變化量。 字母 m 用於表示斜率。 求斜率的公式為:  作為旁註
作為旁註  .
.
斜率為 m 且經過座標  的直線方程為:
的直線方程為:  。 然後只需將方程重新排列成 y = mx + c 的形式。
。 然後只需將方程重新排列成 y = mx + c 的形式。
如果一對直線的斜率相等,則它們平行(符號為  )。 如果它們的斜率相等,則
)。 如果它們的斜率相等,則  。 因此,為了找到平行線的方程,您需要原始線的斜率和平行線上的一組座標。 然後使用點斜式來找到平行線的方程。
。 因此,為了找到平行線的方程,您需要原始線的斜率和平行線上的一組座標。 然後使用點斜式來找到平行線的方程。
兩條直線互相垂直(符號為  ),如果它們的斜率乘積為
),如果它們的斜率乘積為  。因此,如果你需要一條垂直於另一條直線的直線的方程,你只需要用 m 的負倒數替換斜率 m。
。因此,如果你需要一條垂直於另一條直線的直線的方程,你只需要用 m 的負倒數替換斜率 m。
例如,如果直線 1 為 y = 2x + 3,並且你需要找到一條透過點 (0, 1) 的垂直於它的直線,那麼斜率 m = -1/2(因為 2 x -1/2 = -1)。
這給出了 y = -x/2 +c。
將已知點 (0, 1) 代入此方程得到
1 = -0/2 +c,這給出了 c = 1
因此,方程為 y = 1 - x/2。
使用兩點的座標,可以使用勾股定理計算它們之間的距離。任意兩點  和
和  之間的距離 d 由下式給出:
之間的距離 d 由下式給出:
當兩點的座標已知時,中點是這兩點之間中點。對於任意兩點 A 和 B
和 B ,AB 中點的座標可以透過
,AB 中點的座標可以透過  找到。
找到。
只要兩條直線不平行,它們就會在一點相交。你可以透過簡單地 聯立方程 求解兩個方程來找到交點。對於曲線也是如此,儘管非線性曲線可能在多個點相交或根本不相交,並且通常需要不同的方法來求解。
要繪製一條曲線的圖形,你只需要知道曲線的形狀以及其他重要的資訊,如 x 軸和 y 軸的交點以及任何最大值和最小值的點。
 |

|
0 次 - 常數 -  或 或  。在本例中 y=2 。在本例中 y=2 |
1 次 - 線性 -  或 或  。在本例中 y = x。 。在本例中 y = x。 |
 |
|
二次函式 - 二次方 -  . 在這種情況下 y = . 在這種情況下 y =  |
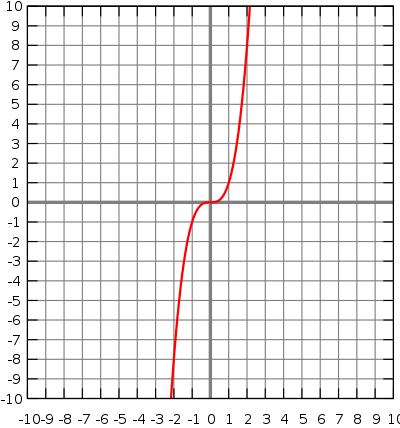
三次函式 - 立方 -  . 在這種情況下 y = . 在這種情況下 y =  |
注意: 所有  的奇數次方具有相同的形狀,從左下角到右上角,所有
的奇數次方具有相同的形狀,從左下角到右上角,所有  的偶數次方具有相同的“桶狀”曲線。
的偶數次方具有相同的“桶狀”曲線。
就像前面一樣,具有  偶數次方的所有曲線具有相同的形狀,具有
偶數次方的所有曲線具有相同的形狀,具有  奇數次方的曲線具有另一種形狀。
奇數次方的曲線具有另一種形狀。
 |

|
 |

|
 |

|
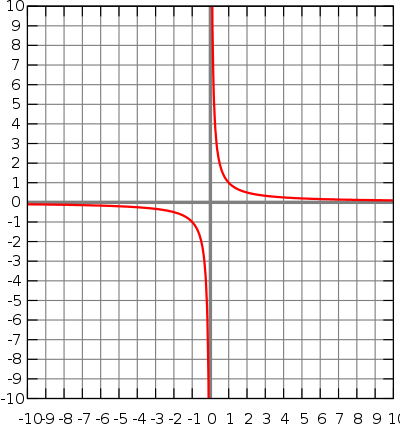
這種形式的所有曲線都沒有  的值,因為
的值,因為  是未定義的。在
是未定義的。在  軸上有漸近線,曲線越來越緩慢地向 y 軸移動,但永遠不會真正接觸到。
軸上有漸近線,曲線越來越緩慢地向 y 軸移動,但永遠不會真正接觸到。

這種形式的所有曲線都沒有 x < 0 的值。它們都具有相同的形狀。
當一條直線與一條曲線相交時,可以透過將直線的方程代入曲線的方程來找到交點。如果直線形如  ,那麼你可以用
,那麼你可以用  替換任何
替換任何  的例項,然後展開方程,然後因式分解得到的二次方程。
的例項,然後展開方程,然後因式分解得到的二次方程。
需要有關描述曲線和直線之間幾何關係的資訊
可以使用與直線和曲線相同的方法。但是,它只適用於簡單的情況。當代數方法失效時,需要求助於圖形方法或數值方法。在考試中,你只需要使用代數方法。
在許多情況下,使用這些規則可以很容易地從現有圖形獲得新圖形。
 是
是  關於 x 軸的對稱圖形。
關於 x 軸的對稱圖形。 是
是  關於 y 軸的對稱圖形。
關於 y 軸的對稱圖形。
 如果
如果  則遠離 y 軸拉伸,如果
則遠離 y 軸拉伸,如果  則向 y 軸拉伸。在這兩種情況下,變化幅度為 b 個單位。
則向 y 軸拉伸。在這兩種情況下,變化幅度為 b 個單位。 如果
如果  則向 x 軸拉伸,如果
則向 x 軸拉伸,如果  則遠離 x 軸拉伸。在這兩種情況下,變化幅度為 a 個單位。
則遠離 x 軸拉伸。在這兩種情況下,變化幅度為 a 個單位。
 是將 f(x) 向右平移 h 個單位後的圖形。
是將 f(x) 向右平移 h 個單位後的圖形。 是將 f(x) 向左平移 h 個單位後的圖形。
是將 f(x) 向左平移 h 個單位後的圖形。 是將 f(x) 向上平移 k 個單位後的圖形。
是將 f(x) 向上平移 k 個單位後的圖形。 是將 f(x) 向下平移 k 個單位後的圖形。
是將 f(x) 向下平移 k 個單位後的圖形。
圓形是平面中所有與給定點(稱為圓心)距離為定值 r 的點的集合。距離 r 是圓形的半徑。

圓形的兩個基本定律是


如果半徑垂直於弦,那麼半徑將平分該弦。

如果圓周上的任意一點與直徑連線,則會形成一個直角三角形。

如果畫出半徑,然後從該點畫出切線,那麼半徑和切線將相互垂直。

圓的標準方程為

這將始終得到一個以原點 (0,0) 為中心的圓。如果我們想要一個以 (h,k) 為中心的圓,則使用以下公式。

但是你不能用計算器繪製這兩個方程。你需要將它分成兩個方程,但圖將不完美,因為當 x = 0 和  :
:  和
和  時,x 未定義。
時,x 未定義。
以下是  的圖形。
的圖形。




































































