有時你無法找到精確答案,只能找到答案所在範圍的估計值。這個答案,以及合適的 **誤差界限**,是可以接受的,並且經常用於實驗資料,因為在實驗資料中,高度的精確性並不總是合理。
如果你被告知某扇門高 2 米,你可以假設這扇門的高度可以在 1.5 米到 2.5 米之間,用 **不等式**  表示,並且實際上是四捨五入到 2 米的。如果你被告知同一扇門高 2.0 米,那麼你可以假設更高的精確度,並說這扇門的高度在 1.95 米到 2.05 米之間,用不等式
表示,並且實際上是四捨五入到 2 米的。如果你被告知同一扇門高 2.0 米,那麼你可以假設更高的精確度,並說這扇門的高度在 1.95 米到 2.05 米之間,用不等式  表示。在這裡你會說門的高度是 2 米,**誤差界限**為
表示。在這裡你會說門的高度是 2 米,**誤差界限**為  。這意味著實際值在宣告值的 0.05m 之內。如果你沒有得到測量值的誤差界限,你應該假設最後一個數字是四捨五入的,並將所有其他數字視為準確的。
。這意味著實際值在宣告值的 0.05m 之內。如果你沒有得到測量值的誤差界限,你應該假設最後一個數字是四捨五入的,並將所有其他數字視為準確的。
門的實際高度的最小值和最大值被稱為 **下界** 和 **上界**,用於確定測量的精度。
**絕對誤差** 是獲得的值和真實值之間的差值。測量的絕對誤差可以使用以下公式找到

**相對誤差** 是絕對誤差佔真實值的比例。測量的相對誤差可以使用以下公式找到

**百分比誤差** 是絕對誤差佔真實值的百分比。測量的百分比誤差可以使用以下公式找到

例如,如果 2 米門的真實值為 1.95 米,則絕對誤差為 ,相對誤差為
,相對誤差為 ,百分比誤差為
,百分比誤差為 .
.
不等式是比較點、線或曲線的相對大小的表示式。與等式不同,等式兩邊始終相等,不等式可以有一邊大於或等於另一邊。
主要有四個基本符號
 小於,
小於, 大於,
大於, 小於或等於,以及
小於或等於,以及 大於或等於。
大於或等於。
例如, 表示
表示 小於 4,
小於 4, 表示
表示 大於 4,
大於 4, 表示
表示 等於 4 或小於 4 的任何數字,而
等於 4 或小於 4 的任何數字,而 表示
表示 等於 4 或大於 4 的任何數字。
等於 4 或大於 4 的任何數字。
注意 和
和 本質上是相同的陳述。
本質上是相同的陳述。
如果您對哪個符號表示小於和大於是感到困惑,那麼記住不等式符號始終指向較小的數字會很有幫助。要記住的一條基本規則是,如果除以或乘以負數,不等式符號就會反轉。例如 將變為
將變為 。這是有道理的,因為 -4 大於 -5,而 5 大於 4。
。這是有道理的,因為 -4 大於 -5,而 5 大於 4。
在某些情況下,兩個不等式可以合併成一個。例如,門的高度據說在  和
和  之間。通常的寫法是
之間。通常的寫法是  。注意不等號的方向是一致的。
。注意不等號的方向是一致的。  是完全可以接受的,但將方向相反的不等式合併是不正確的,必須將它們作為兩個獨立的不等式保留。
是完全可以接受的,但將方向相反的不等式合併是不正確的,必須將它們作為兩個獨立的不等式保留。
為了解線性不等式,只需將 x 隔離。例如: 


注意符號的變化。
為了解二次不等式,我們需要:1)將不等式設為零。
2)因式分解方程並找到零點。
3)用方程的零點作為唯一點建立數軸。在這些點之間建立區間。
4)找到因式的符號。然後找到方程在區間上的符號。
5)滿足不等式的區間是你的答案集。
例如:找到滿足關係  的區間。
的區間。
步驟 1:
步驟 2: ,因此零點將是 -1 和 5
,因此零點將是 -1 和 5
步驟 3
編輯:需要新的圖片來顯示中間列為:x 大於或等於 -1 且小於或等於 5。
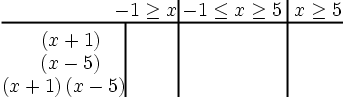
步驟 4:
步驟 5:滿足該關係的區間是  和
和  。這是解集。
。這是解集。
解涉及分數的方程與解二次不等式非常相似。當您解涉及分數的不等式時,不能交叉相乘(因為您可能在乘以一個負數,這將反轉不等式的符號)。這將導致錯誤的答案。還要記住,分母永遠不能為零。
例如:找到滿足關係  的區間。
的區間。
步驟 1: 將  簡化後得到
簡化後得到  .
.
步驟 2: 已經因式分解,所以零點為 -1 和 5。
步驟 3:
步驟 4:
步驟 5: 滿足關係式的區間是  和
和  ,因此
,因此  。注意,
。注意, 大於是因為 x 不能等於 -1,否則分母將為零。
大於是因為 x 不能等於 -1,否則分母將為零。
區間表示法是另一種寫不等式問題的解集區間的方法。應該使用區間表示法給出答案,因為它更容易理解。在區間表示法中,解集用括號給出。使用兩種型別的括號:
( ) 這類括號表示端點不包含在解集中。  和
和 
[ ] 這類括號表示端點包含在解集中。  和
和 
還可以使用這些括號的各種組合。如果有多個區間,需要使用數學並集符號  。此外,如果區間到達
。此外,如果區間到達  ,則需要使用圓括號 ),因為
,則需要使用圓括號 ),因為  是一個概念,而不是一個數字。
是一個概念,而不是一個數字。
例如,將  轉換為區間表示法。
轉換為區間表示法。
在區間表示法中,解集變為 ![{\displaystyle \left(-\infty ,-4\right)\cup \left[-3,7\right)\cup \left(8,9\right]\cup \left[12,\infty \right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5d111db3b2d335b733e41291e8825ab741bc9ea) ,正如您所見,這更容易理解。
,正如您所見,這更容易理解。
















































![{\displaystyle \left(-\infty ,-4\right)\cup \left[-3,7\right)\cup \left(8,9\right]\cup \left[12,\infty \right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5d111db3b2d335b733e41291e8825ab741bc9ea)