分形/複平面迭代/層疊

層疊是一種用於研究多項式動力學的工具（模型）。 這裡，倍增對映 用於分析復二次多項式 的動力學。它比復二次對映更容易分析的動力系統。

週期軌道

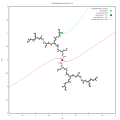
角度在倍增對映 下的週期軌道

注意，這裡連線單位圓上 2 個點 z1 和 z2 的弦意味著 $z_{2}=z_{1}^{2}$。這並不意味著這些點是同一條射線的著陸點。

一些軌道不交叉

• 
  週期 2 軌道（角度在倍增對映下）
• 
  週期 3 軌道（角度在倍增對映下）
• 
  週期 4 軌道（角度在倍增對映下）
• 
  週期 5 軌道（角度在倍增對映下）
• 
  週期 6 軌道（角度在倍增對映下）

但有些則交叉

• 
  11/63 在倍增對映下的週期 6 軌道
• 
  74/511 在倍增對映下的週期 9 軌道

軌道肖像

軌道肖像可以有兩種形式

• 數字列表 ( 具有偶數分母的普通分數)
• 影像顯示射線著陸在週期性 z 點上 (= 動態平面劃分)

注意

• 這裡連線單位圓上 2 個點 z1 和 z2 的弦意味著這些點是同一條射線的著陸點。這並不意味著 $z_{2}=z_{1}^{2}$.
• 軌道肖像是軌道的肖像，它在復二次對映下是週期的。
• Julia 集有許多週期軌道，因此它也有許多軌道肖像
• 軌道肖像是軌道的組合描述
• (杜瓦迪和哈伯德)。二次多項式 fc 的每一個排斥和拋物線週期點都是具有有理角的外射線的著陸點。反之，每一個具有有理角的外射線要麼著陸在 J(fc) 中的週期點，要麼著陸在預週期點。

影像

影像可以有三種形式

• 動態平面的影像，包含 Julia 集和著陸在週期軌道上的外射線
• 上述影像的草圖
  • 標準方式: 軌道的點繪製在單位圓內，射線由連線角度 ( 單位圓上的點) 和軌道點的線組成。它看起來像上述影像的草圖
  • 雙曲方式: 點位於單位圓上，這裡連線單位圓上 2 個點 z1 和 z2 的弦意味著這些點是同一條射線的著陸點。這並不意味著 $z_{2}=z_{1}^{2}$。弦使用弧 ( 正交圓的一部分) 繪製。

動態平面由動態射線劃分

該劃分是由角度為 $\theta /2$ 和 $(\theta +1)/2$ 的動態射線形成的，它們共同著陸在臨界點。

劃分

• 在定義揉捏序列時使用的劃分：將開單位圓盤（或圓群）S1 分為兩部分：$\theta /2$ 和 $(\theta +1)/2$（角度加倍的兩個逆像）；
  • 包含角度 0 的開部分標為 0
  • 另一個開部分標為 1
  • 邊界得到標籤 ⋆
• 動態平面透過動態射線的對應劃分，這裡以一個Misiurewicz多項式為例

• 
  1/4
• 
  1/6
• 
  9/56
• 
  129/16256

如何找到落在臨界值 z = c 上的動態外部射線的角度？

動力平面的層壓

"層壓是由 Thurston 在 1980 年代初引入多項式動力學領域的"用於顯示外部射線的著陸模式。

層壓 L 給出

• 二次對映動力學的組合描述。 因為單位圓上的加倍對映作用是復多項式在複平面上的作用模型
• Julia 集的精確拓撲結構 = Julia 集的拓撲模型
• 射線肖像的模型。在層壓中的角度的外部射線落在 Julia 集/Mandelbrot 集的"切點"。

注意，這裡連線單位圓上兩點 z1 和 z2 的弦意味著這兩點是同一射線的著陸點。這並不意味著 $z_{2}=z_{1}^{2}$.

對於二次多項式，初始集的形式為：

$\left\{\theta ,\theta +{\frac {1}{2}}\right\rbrace$

?????

定義

層壓由以下組成

• 閉單位圓盤 D2
• 連線邊界圓上兩點（角度以圈數表示）的雙曲弧（或葉）。這些角度的外部射線（在動力平面上）落在同一點上

平面上單位圓盤的層壓是單位圓盤內弦（葉，弧）的閉合集合

二次層壓 = 在角度加倍對映下保持不變的那些

符號

• $\sigma _{d}$ 是一個對映，在 d=2 的情況下，它是週期加倍對映
• 弦 = 葉 = 單位圓盤上識別（連線）單位圓上兩點的連續路徑
  • 主葉 是
    • 層壓中最大長度的葉
    • 最接近 1/2 的長度
  • 次葉 是主葉的像
  • 臨界弦：一個$\sigma _{d}$-臨界弦是 $D$ 的弦，其端點在 $\sigma _{d}$ 下對映到同一點
• 拉回 = 拉回過程 = 反向迭代
• 樹狀二次多項式的次標籤 = 假設 pc = z^2 + c 是一個樹狀二次多項式；所有點 a ∈ S^1 滿足 φ(a) = c 的凸包 Gc 被稱為 pc 的次標籤。

層壓的性質

層壓必須滿足以下規則

• 葉不會交叉，但它們可能共享端點
• 層壓是正向和反向不變的（在加倍對映下）

層壓的不變性

"單位圓盤中層壓 L 的不變性意味著

• 只要有 L 的一片葉子連線 $z_{1}$ 和 $z_{2}$，也有一片 L 的葉子連線 $z_{1}^{2}$ 和 $z_{2}^{2}$。
• 只要有一條連線 $z_{1}$ 和 $z_{2}$ 的弦，則存在點 $\pm z_{3}^{2}$ 和 $\pm z_{4}^{2}$，其中 $z_{3}^{2}=z_{1}$ 和 $z_{4}^{2}=z_{2}$，並且存在 L 的葉子連線 z3 到 z4，以及 -z3 到 -z4。

工具

用於研究層壓結構動力學的工具

• 中央帶引理

繪製層壓結構

• Drawlam：由 Clinton P. Curry 編寫的用於渲染層壓結構的程式。 該程式在修改後的 BSD 樣式許可下獲得許可。它使用輸入檔案或從控制檯讀取。
  • bitbucket 官方倉庫
  • gitlab 非官方倉庫
• 不變層壓結構計算器 Java applet 由 Danny Calegari 編寫。它計算曼德勃羅集邊界上連線的茱莉亞集的不變層壓結構，外部角可變。附有 Java 原始碼
• 層壓結構 由 Danny Calegari 編寫。使用標準 Xlib 東西的 X11 Cpp 程式。原始碼根據 GNU GPL 的條款釋出。該程式是一個用於對圓形層壓結構進行實驗的玩具。以符號和影像形式表示它。它只需要一個輸入：層壓結構的大小（多邊形端點的數量）。這些端點按逆時針順序從 0 到 size-1 列舉。對於每個端點，nextleaf 指向逆時針方向的相鄰端點。

我在 main.cc 中進行了更改

#include <math.h>
#include <iostream> // I have removed .h
#include <stdlib.h>
#include "graphics.cc"
using namespace std; // added because : main.cc:101: error: ‘cout’ was not declared in this scope

然後在 program 目錄中

make
./lamiantion

示例

樹枝狀層壓結構

• c = i
• 位於 $z={\frac {1-{\sqrt {1-4i}}}{2}}$ 的點稱為
  • 被稱為
    • 主三重點
    • 固定點，因為它在對映 $f(z)=z^{2}+i$ 下保持不變
  • 在 1/7、2/7 和 4/7 處有外部射線，這些射線在直接到達之前，會形成一個圍繞該點的無限對數螺旋。
• 中央池點在 1/12 和 7/12 處有外部射線
• 在 φ 下，任何三重點都不會被對映到池中，反之亦然。
• 我們只關心作為三重點或池的夾點。
• 如果樹枝上的一個點是兩條外部射線的著陸點，這兩條外部射線的角度都具有 ${\frac {k}{12*2n}}$ 的形式，其中 k、n ∈ N，且 k ≡ 1 mod 6，則該點被稱為 **池**。
• 如果樹枝上的一個點被移除後會將樹枝分成三個連通分量，則該點被稱為 **三叉點**。這樣的點是三條外部射線的著陸點，這些射線的角度都具有 ${\frac {k}{7*2n}}$ 的形式，其中 k、n ∈ N，且 k 模 7 同餘於 1、2 或 4。

演算法

• “我們從單位圓開始，就像之前一樣，如果某個點是三叉點或池，我們就在圓上連線任何兩個外部射線落在該點的點之間的弧線。”
• 因此，我們將 1/7、2/7 和 4/7 這三個點連線成一個三角形，並將 1/12 和 7/12 這兩個點連線成一條弧線。
• 我們繼續以這種方式，為三叉點繪製更多三角形，為池繪製更多弧線。”

圖片

• z2 + i 的層壓，來自 Curtis T McMullen 的畫廊

二階割點

週期為一的軌道 = 不動點（巴西利卡層壓）

對於所有引數 c 在曼德爾布羅特集合中由射線 1/3 和 2/3 所圍成的尾流區域內的復二次多項式 $f_{c}(z)$，都存在一個排斥不動點，其軌道肖像為

${\mathcal {P}}({\mathcal {O}})=\left\{{\mathcal {A}}_{1}\right\rbrace =\left\{\left({\frac {1}{3}},{\frac {2}{3}}\right)\right\rbrace$

• 
  落在不動點 alpha 上的外部射線
• 
  由落在週期為 1 軌道上的兩條射線對圓進行的劃分（角度在倍增對映下的值）
• 
  與巴西利卡朱利亞集 $f_{c}(z)=z^{2}-1$ 相關的二次不變層壓 ${\frac {1}{3}}$
• 
  落在割點上的射線

“巴西利卡只有一種型別的夾點，並且在層壓中弧線之間存在間隙”。——威爾·史密斯

演算法

• 我們從單位圓開始，
• 新增連線 1/3 和 2/3 的弧線（小葉 = 包含曼德爾布羅特集合週期為 2 分量的尾流區域的角度）
• 1/6 和 5/6，以及所有具有 ${\frac {3k-1}{3*2^{n}}},{\frac {3k+1}{3*2^{n}}}$ 形式的每一對有理數的其它對（對於某個整數 k、n）
• 當我們完成時，我們就生成了巴西利卡的不變層壓。

週期點：週期為一（排斥 = 在朱利亞集中）

• 不動點 $\alpha$。這裡，兩個不動點 $z=\alpha ={\frac {1-{\sqrt {5}}}{2}}$ 之一是兩條外部射線 1/3 和 2/3 的著陸點。這些是週期射線（前週期 = 0，週期 = 2）。請注意，著陸點的週期不等於落在其上的射線的週期。
• 點 $z=-\alpha$ 是兩條射線 1/6 和 5/6 的著陸點。這些是前週期射線：前週期 = 1，週期 = 2

週期為 2（超吸引 = 分量的中心）。這些點是兩個主要分量的中心。它們的前像就是其他分量的中心。

• 臨界點 z = 0
• 臨界值 z = -1

z = 0.000000000000000 + 0.521555030187677 * i 的前週期為 3，週期為 1。它是

• 以 z = 0 為中心的連通分量的內部射線 1/4
• 前週期為 3，週期為 2 的外部射線 5/24（001p10）和 7/24 的著陸點。

z = 0.000000000000000 -0.521555030187677 i 的前週期為 3，週期為 1。它是以下的著陸點：

• 內部射線 3/4
• 外部射線 17/24 或 101p10 和 19/24，它們的前週期 = 3，週期 = 2。

z = 0.334146940762091 +0.378310439392182 i 的前週期為 5，週期為 1。它是以下的著陸點：

• 內部射線 1/8
• 外部射線 角度 17/96 或 00101p10 和 19/96 的前週期 = 5，週期 = 2。

$\Psi (x)={\begin{cases}2x-k&{\text{if }}x\in [k+1/3,k+2/3],k\in \mathbb {Z} \\(x+k+1)/2&{\text{if }}x\in (k-1/3,k+1/3),k\in \mathbb {Z} \end{cases}}$

3 階切割點

週期一軌道 = 固定點

在二次對映下的軌道包含一個（固定點）

${\mathcal {O}}=\left\{z_{1}\right\rbrace =\left\{\alpha _{c}\right\rbrace$

這個點是 3 個外部射線的著陸點，並且具有軌道肖像

${\mathcal {P}}({\mathcal {O}})=\left\{{\mathcal {A}}_{1}\right\rbrace =\left\{\left({\frac {1}{7}},{\frac {2}{7}},{\frac {4}{7}}\right)\right\rbrace$

• 
  動態平面的分割槽：杜阿迪兔子朱利亞集和落在固定點上的外部射線 $\alpha _{c}\,$
• 
  軌道肖像以雙曲方式製作。由週期 3 軌道對圓進行分割槽（在倍增對映下的角度）
• 
  與兔子朱利亞集相關的層壓 $L_{\frac {1}{7}}$

週期 2 軌道

c 是曼德勃羅集在週期 2 和 6 元件之間的根點：

$c=-1+{\frac {1}{4}}e^{2\pi i{\frac {2}{3}}}\in \partial M$

內部地址為 1-2-6。

六個週期射線週期落在二週期拋物線軌道上

${\mathcal {O}}=\left\{z_{2,1},z_{2,2}\right\rbrace$

其中

$z_{2,1}=-{\frac {1}{2}}+{\frac {1}{2}}{\sqrt {1-e^{2\pi i{\frac {2}{3}}}}}$

$z_{2,2}=-{\frac {1}{2}}-{\frac {1}{2}}{\sqrt {1-e^{2\pi i{\frac {2}{3}}}}}$

軌道肖像

${\mathcal {P}}({\mathcal {O}})=\left\{{\mathcal {A}}_{1},{\mathcal {A}}_{2}\right\rbrace =\left\{\left({\frac {22}{63}},{\frac {25}{63}},{\frac {37}{63}}\right),\left({\frac {44}{63}},{\frac {50}{63}},{\frac {11}{63}}\right),\right\rbrace$

• 
  引數平面被落在內地址為 1-2-6 的根點上的射線分割
• 
  動態平面被落在拋物線軌道上的射線分割
• 
  圓被週期 6 軌道分割（角度在倍增對映下）

週期 3 軌道

引數 c 是 Mandelbrot 集合中週期 9 雙曲分量的中心

$c=-0.03111+0.79111*i$

二次對映下的軌道由 3 個點組成

${\mathcal {O}}=\left\{z_{3,1},z_{3,2},z_{3,1}\right\rbrace$

與拋物線週期 3 軌道 ${\mathcal {O}}$ 相關的軌道肖像是：

${\mathcal {P}}({\mathcal {O}})=\left\{{\mathcal {A}}_{1},{\mathcal {A}}_{2},{\mathcal {A}}_{3}\right\rbrace =\left\{\left({\frac {74}{511}},{\frac {81}{511}},{\frac {137}{511}}\right),\left({\frac {148}{511}},{\frac {162}{511}},{\frac {274}{511}}\right),\left({\frac {296}{511}},{\frac {324}{511}},{\frac {37}{511}}\right)\right\rbrace$

化合價 = 每個軌道點 3 個射線（= 每個點都是 3 個外部射線的著陸點）

上述角度對應的射線落在該軌道的點上。

• 
  動態平面分割：Julia 集和落在週期 3 軌道上的外部射線
• 
  74/511 在倍增對映下的軌道

5 階切割點

週期 1 軌道 = 不動點

• 
  週期 5 超吸引軌道 = c 是週期 5 分量軌道的中心：{5/31 , 10/31 , 20/31 , 9/31 , 18/31}
• 
  軌道：{5/31 , 10/31 , 20/31 , 9/31 , 18/31}，交叉
• 
  1/31 在倍增對映下的軌道，不交叉，= {1/31 , 2/31 , 4/31 , 8/31 , 16/31}。引數 c 將位於內角為 2/5 的拋物線點上

問題

• 如何計算軌道肖像？
• 當我在 Mandelbrot 集合內部移動時，軌道肖像如何變化？
  • 在 Mandelbrot 集合內部的連通分量中，層化是相同的
• 射線共同著陸的準則
  • 由 JINSONG ZENG 在動態平面上提出的射線共同著陸的準則
  • 在引數平面上（尾流角度和共軛角度）

參見

• 層化
• Mandelbrot 集合的層化
• Douady 兔
• 軌道肖像
• 根和拋物線不動點：外部射線
• (單位) 圓的鑲嵌，拼貼
• 非交叉圓分割
• benice 的螺旋
• 自相似群

參考文獻

• CURTIS T MCMULLEN 的影像庫中 z2 + i 的層狀結構
• 不變因子、茱莉亞等價性和 (抽象) 曼德勃羅集 KARSTEN KELLER 撰寫。書籍來自系列講座筆記系列

第 1732 卷，2000 年，DOI：10.1007/BFb0103999。施普林格出版社，柏林-海德堡-紐約 2000 年