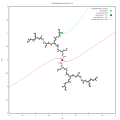
分形/複平面迭代/動態外射線

影像

• 落在alpha不動點上的射線
• 
  雙可達
• 
  三可達

• 落在臨界點和臨界值上的射線
• 
  1/4
• 
  1/6
• 
  9/56
• 
  129/16256

理論

令$\Psi _{c}\,$ 為從閉合單位圓盤${\overline {\mathbb {D} }}$ 的補集（外部）到填充的Julia集$\ K_{c}$ 的補集的對映（保角對映，同構）。

$\Psi _{c}:{\hat {\mathbb {C} }}\setminus {\overline {\mathbb {D} }}\to {\hat {\mathbb {C} }}\setminus K_{c}$

其中${\hat {\mathbb {C} }}$ 表示黎曼球面（擴充套件複平面）。

令$\Psi _{c}=\Phi _{c}^{-1}\,$ 表示

• 逆Boettcher對映
• 黎曼對映

角度為$\theta \,$ 的外射線記為${\mathcal {R}}_{\theta }^{K}$ 是

• 在$\Psi _{c}\,$ 下的直線${\mathcal {R}}_{\theta }=\{\left(r\cdot e^{2\pi i\theta }\right):\ r>1\}$ 的像

${\mathcal {R}}_{\theta }^{K}=\Psi _{c}({\mathcal {R}}_{\theta })$

• 具有相同外部角 $\theta$ 的填充後的 Julia 集外部的點集

${\mathcal {R}}_{\theta }^{K}=\{z\in {\hat {\mathbb {C} }}\setminus K_{c}:\arg(\Phi _{c}(z))=\theta \}$

重要問題

哪些是獨特的射線？

• "落在 Julia 集的關鍵點（或包含關鍵點的球體的根點）上的射線 t 對該 Julia 集是唯一的，因此是識別 Julia 集的一種方式。因此，我用 t 來命名 Julia 集 Jc。在餘下部分中，我只能處理 t=p/q 為有理數的 Julia 集。"
• 臨界前週期多項式通常由 落在臨界值的外部射線 的角度 $\theta$ 進行引數化

如何逼近外部射線？

• 用於 Julia 集的二進位制分解方法 (BDM/J)
• 場線 的標量場（勢）
• SAM = 條帶平均方法 基本上是計算角度的一種廉價方式。

• 
• 
  BDM 的邊界
• 
  SAM

在 BDM 影像中，角度（以圈數測量）的外部射線

$angle=(k/2^{n})~~{\mbox{mod }}~1\,$

可以看作子集的邊界。

當兩個外部動態射線落在同一點時

問題：

• Q1：給定 Julia 集中的一個點，有多少條射線落在該點上？
• Q2：給定兩條射線 $R_{\theta _{1}}$ 和 $R_{\theta _{2}}$，在什麼條件下它們落在同一點？
  • 當外部射線落在同一點時
  • 著陸等效性 = 哪些射線落在同一點？
  • 數值標準 = 它們具有相同的（數值）著陸點
• Q3：哪些射線支援相同的 Fatou 分量？

定理 1.2 設 f 為度數 d ≥ 2 的多項式，其 Julia 集區域性連通。如果兩個角度 $\theta _{1}$ 和 $\theta _{2}$ 關於臨界肖像具有相同的行程，那麼外部射線 $R_{\theta _{1}}$ 和 $R_{\theta _{2}}$ 的著陸點要麼重合，要麼屬於 Fatou 域的邊界，該邊界最終被迭代到 Siegel 盤上。

如何找到落在臨界值 z= c 上的外部射線的角度呢？

這取決於具體情況。

• 例如，當引數 c 是一個 Misiurewicz 點時，可以使用組合方法。
• 大多數情況下，你首先構造角度，然後確定引數。
• 但是，如果你想從 Julia 集或 Hubbard 樹中讀取角度，你可以按照 Mandel 程式 中的 Demo 4 第 1 和 2 頁的說明進行。

構造 填充 Julia 集 的脊柱

構造脊柱的演算法由 A. Douady 描述

• 連線 $-\beta \,$ 和 $\beta \,$,
• (待完成)

• 

繪製外部射線是什麼意思呢？

這意味著

• 計算（近似）射線的某些點
• 用線段連線這些點

這將給出射線 ${\mathcal {R}}$ 的近似值。

繪製 動態外部射線

演算法

• 牛頓法
• 逆向迭代
• Boettcher 對映的逆對映
• 追蹤角度為 t 的外部射線（曲線）

逆向迭代

對復二次多項式進行反向迭代，並適當選擇前像

週期為 2-40 的落在 α 固定點上的週期性外部射線。使用反向迭代生成。

這種方法已經被許多人使用，並被 Thierry Bousch 證明。

Wolf Jung 的 C++ 程式碼可以在 qmnplane.cpp 檔案中的 QmnPlane::backray() 函式中找到（參見 Mandel 程式 的原始碼）。

• 週期性角度的射線（最簡單的情況）

我們將透過一個例子來解釋它

首先選擇外部角度 $t\,$ （以圈數為單位）。週期性射線的外部角度是一個有理數。

$t={\frac {1}{3}}\,$

計算外部角度在 倍增對映 下的週期。

因為 "1/3 的倍增結果是 2/3，而 2/3 的倍增結果是 4/3，它與 1/3 同餘"

$1\equiv 2{\pmod {3}}.\,$

或者

${\frac {2}{3}}\equiv {\frac {1}{3}}{\pmod {1}}.\,$

因此外部角 $t={\frac {1}{3}}\,$ 在倍增對映下週期為2。

從無窮遠處的兩個點開始（在共軛平面上）

在射線 1/3 上有一個點 $w=R*e^{2\pi i/3}\,$

在射線 2/3 上有一個點 $w=R*e^{4\pi i/3}\,$.

在無窮遠附近 $z=w\,$ 因此可以切換到動力學平面（博特切爾共軛）

向後迭代（從兩個可能性中適當選擇） 在射線 1/3 上的點會到射線 2/3，再回到 1/3，依此類推。

在 C 語言中是 

/* choose one of 2 roots: zNm1 or -zNm1  where zN = sqrt(zN - c )  */
if (creal(zNm1)*creal(zN) + cimag(zNm1)*cimag(zN) <= 0) zNm1=-zNm1;

或者在 Maxima CAS 

if (z1m1.z01>0) then z11:z1m1 else z11:-z1m1;

必須將點集分成 2 個子集（2 條射線）。繪製這兩個集合中的一個，並將這些點連線起來。它將近似於射線。

• 對於預週期角的射線（待完成）

/*

compute last point ~ landing point
of the dynamic ray for periodic angles ( in turns )

 gcc r.c -lm -Wall -march=native

landing point of ray for angle = 1 / 15 = 0.0666666666666667 is = (0.0346251977103306 ;  0.4580500411138030 ) ; iDistnace = 18 
landing point of ray for angle = 2 / 15 = 0.1333333333333333 is = (0.0413880816505388 ;  0.5317194187688231 ) ; iDistnace = 17 
landing point of ray for angle = 4 / 15 = 0.2666666666666667 is = (-0.0310118081927549 ;  0.5440125864026020 ) ; iDistnace = 17 
landing point of ray for angle = 8 / 15 = 0.5333333333333333 is = (-0.0449867688014234 ;  0.4662592852362425 ) ; iDistnace = 18

*/

// https://gitlab.com/adammajewski/ray-backward-iteration
#include <stdio.h>
#include <stdlib.h> // malloc
#include <math.h> // M_PI; needs -lm also 
#include <complex.h>

/* --------------------------------- global variables and consts ------------------------------------------------------------ */
#define iPeriodChild 4 // iPeriodChild of secondary component joined by root point

// - --------------------- functions ------------------------

/* 
   principal square  root of complex number 
   wikipedia  Square_root

   z1= I;
   z2 = root(z1);
   printf("zx  = %f \n", creal(z2));
   printf("zy  = %f \n", cimag(z2));
*/
double complex root(double x, double y)
{ 
  
  double u;
  double v;
  double r = sqrt(x*x + y*y); 
  
  v = sqrt(0.5*(r - x));
  if (y < 0) v = -v; 
  u = sqrt(0.5*(r + x));
  return u + v*I;
}

// This function only works for periodic  angles.
// You must know the iPeriodChild n before calling this function.
// draws all "iPeriodChild" external rays 
// commons  File:Backward_Iteration.svg
// based on the code by Wolf Jung from program Mandel
// http://www.mndynamics.com/

int ComputeRays( //unsigned char A[],
			    int n, //iPeriodChild of ray's angle under doubling map
			    int iterMax,
                            double Cx, 
                            double Cy,
                            double dAlfaX,
                            double dAlfaY,
                            double PixelWidth,
                            complex double zz[iPeriodChild] // output array

			    )
{
  double xNew; // new point of the ray
  double yNew;
  
  const double R = 10000; // very big radius = near infinity
  int j; // number of ray 
  int iter; // index of backward iteration

  double t,t0; // external angle in turns 
  double num, den; // t = num / den
  
  double complex zPrev;
  double u,v; // zPrev = u+v*I
 
  int iDistance ; // dDistance/PixelWidth = distance to fixed in pixels

  
  /* dynamic 1D arrays for coordinates ( x, y) of points with the same R on preperiodic and periodic rays  */
  double *RayXs, *RayYs;
  int iLength = n+2; // length of arrays ?? why +2

  //  creates arrays :  RayXs and RayYs  and checks if it was done
  RayXs = malloc( iLength * sizeof(double) );
  RayYs = malloc( iLength * sizeof(double) );
  if (RayXs == NULL || RayYs==NULL)
    {
      fprintf(stderr,"Could not allocate memory");
      getchar(); 
      return 1; // error
    }

   // external angle of the first ray 
   num = 1.0;
   den = pow(2.0,n) -1.0;
   t0 = num/den; // http://fraktal.republika.pl/mset_external_ray_m.html
   t=t0;
   // printf(" angle t = %.0f / %.0f = %f in turns \n", num, den, t0);

  //  starting points on preperiodic and periodic rays 
  //  with angles t, 2t, 4t...  and the same radius R
  for (j = 0; j < n; j++)
    { // z= R*exp(2*Pi*t)
      RayXs[j] = R*cos((2*M_PI)*t); 
      RayYs[j] = R*sin((2*M_PI)*t);
      //
      // printf(" %d angle t = = %.0f / %.0f =  %.16f in turns \n", j, num , den,  t); 
      //
      num *= 2.0;
      t *= 2.0; // t = 2*t
      if (t > 1.0) t--; // t = t modulo 1
      
    }
  //zNext = RayXs[0] + RayYs[0] *I;

  // printf("RayXs[0]  = %f \n", RayXs[0]);
  // printf("RayYs[0]  = %f \n", RayYs[0]);

  // z[k] is n-periodic. So it can be defined here explicitly as well.
  RayXs[n] = RayXs[0]; 
  RayYs[n] = RayYs[0];

  //   backward iteration of each point z
  for (iter = -10; iter <= iterMax; iter++)
    { 
     	
      for (j = 0; j < n; j++) // n +preperiod
	{ // u+v*i = sqrt(z-c)   backward iteration in fc plane 
	  zPrev = root(RayXs[j+1] - Cx , RayYs[j+1] - Cy ); // , u, v
	  u=creal(zPrev);
	  v=cimag(zPrev);
                
	  // choose one of 2 roots: u+v*i or -u-v*i
	  if (u*RayXs[j] + v*RayYs[j] > 0) 
	    { xNew = u; yNew = v; } // u+v*i
	  else { xNew = -u; yNew = -v; } // -u-v*i

	  // draw part of the ray = line from zPrev to zNew
	 // dDrawLine(A, RayXs[j], RayYs[j], xNew, yNew, j, 255);
                
	  
	  //  
	  RayXs[j] = xNew; RayYs[j] = yNew;
                
	

                
	} // for j ...

          //RayYs[n+k] cannot be constructed as a preimage of RayYs[n+k+1]
      RayXs[n] = RayXs[0]; 
      RayYs[n] = RayYs[0];
          
      // convert to pixel coordinates 
      //  if z  is in window then draw a line from (I,K) to (u,v) = part of ray 
   
      // printf("for iter = %d cabs(z) = %f \n", iter, cabs(RayXs[0] + RayYs[0]*I));
     
    }

  // Approximate end of ray by straight line to it's landing point here = alfa fixed point
 // for (j = 0; j < n + 1; j++)
  //  dDrawLine(A, RayXs[j],RayYs[j], dAlfaX, dAlfaY,j, 255 );

  // this check can be done only from inside this function
  t=t0;
  num = 1.0;
  for (j = 0; j < n ; j++)
    {

      zz[j] = RayXs[j] +  RayYs[j] * I; // save to the output array
      // Approximate end of ray by straight line to it's landing point here = alfa fixed point
      //dDrawLine(RayXs[j],RayYs[j], creal(alfa), cimag(alfa), 0, data); 
      iDistance = (int) round(sqrt((RayXs[j]-dAlfaX)*(RayXs[j]-dAlfaX) +  (RayYs[j]-dAlfaY)*(RayYs[j]-dAlfaY))/PixelWidth);
      printf("last point of the ray for angle = %.0f / %.0f = %.16f is = (%.16f ;  %.16f ) ; Distance to fixed = %d  pixels \n",num, den, t, RayXs[j], RayYs[j],  iDistance);
      num *= 2.0;
      t *= 2.0; // t = 2*t
      if (t > 1) t--; // t = t modulo 1
    } // end of the check

  // free memmory
  free(RayXs);
  free(RayYs);

  return  0; //  
}

int main()
{
  
  complex double l[iPeriodChild];
  int i;
  // external angle in turns = num/den; 
  double num = 1.0;
  double den = pow(2.0, iPeriodChild) -1.0;

   ComputeRays( iPeriodChild, 
                   10000, 
                   0.25, 0.5, 
                   0.00, 0.5,
                   0.003,
                   l ) ;

  
  printf("\n see what is in the output array : \n");

  for (i = 0; i < iPeriodChild ; i++) {
       printf("last point of the ray for angle = %.0f / %.0f = %.16f is = (%.16f ;  %.16f ) \n",num, den, num/den, creal(l[i]), cimag(l[i]));
       num *= 2.0;}

  return 0;
}

執行它 

./a.out

輸出 

last point of the ray for angle = 1 / 15 = 0.0666666666666667 is = (0.0346251977103306 ;  0.4580500411138030 ) ; Distance to fixed = 18  pixels 
last point of the ray for angle = 2 / 15 = 0.1333333333333333 is = (0.0413880816505388 ;  0.5317194187688231 ) ; Distance to fixed = 17  pixels 
last point of the ray for angle = 4 / 15 = 0.2666666666666667 is = (-0.0310118081927549 ;  0.5440125864026020 ) ; Distance to fixed = 18  pixels 
last point of the ray for angle = 8 / 15 = 0.5333333333333333 is = (-0.0449867688014234 ;  0.4662592852362425 ) ; Distance to fixed = 19  pixels

 see what is in the output array : 
last point of the ray for angle = 1 / 15 = 0.0666666666666667 is = (0.0346251977103306 ;  0.4580500411138030 ) 
last point of the ray for angle = 2 / 15 = 0.1333333333333333 is = (0.0413880816505388 ;  0.5317194187688231 ) 
last point of the ray for angle = 4 / 15 = 0.2666666666666667 is = (-0.0310118081927549 ;  0.5440125864026020 ) 
last point of the ray for angle = 8 / 15 = 0.5333333333333333 is = (-0.0449867688014234 ;  0.4662592852362425 )

射線上的點正在向後移動

• 當它離茱莉亞集合很遠時，速度很快
• 靠近茱莉亞集合時速度很慢（經過 50 次迭代後，點之間的距離 = 0 畫素）

參見計算示例（這裡 畫素大小 = 0.003） 

# iteration distance_between_points_in_pixels
0 	 3300001 
1 	 30007 
2 	 2296 
3 	 487 
4 	 179 
5 	 92 
6 	 54 
7 	 34 
8 	 23 
9 	 18 
10 	 14 
11 	 11 
12 	 9 
13 	 7 
14 	 6 
15 	 5 
16 	 5 
17 	 4 
18 	 4 
19 	 3 
20 	 3 
21 	 3 
22 	 3 
23 	 2 
24 	 2 
25 	 2 
26 	 2 
27 	 2 
28 	 2 
29 	 2 
30 	 1 
31 	 1 
32 	 1 
33 	 1 
34 	 1 
35 	 1 
36 	 1 
37 	 1 
38 	 1 
39 	 1 
40 	 1 
41 	 1 
42 	 1 
43 	 1 
44 	 1 
45 	 1 
46 	 1 
47 	 1 
48 	 1 
49 	 1 
50 	 1 
51 	 1 
52 	 1 
53 	 1 
54 	 1 
55 	 1 
56 	 0 
57 	 0 
58 	 0 
59 	 0 
60 	 0 

可以選擇畫素大小不同的點 

#iteration    distance(z1,z2)   distance (z,alfa)
       0 	 3300001 	 33368
       1 	   30007 	  3364
       2 	    2296 	  1074
       3 	     487 	   591
       4 	     179 	   413
       5 	      92 	   321
       6 	      54 	   267
       7 	      34 	   234
       8 	      23 	   211
       9 	      18 	   193
      10 	      14 	   179
      11 	      11 	   169
      12 	       9 	   160
      13 	       7 	   153
      14 	       6 	   146
      15 	       5 	   141
      16 	       5 	   136
      17 	       4 	   132
      18 	       4 	   128
      19 	       3 	   125
      20 	       3 	   122
      21 	       3 	   119
      22 	       3 	   117
      23 	       2 	   115
      24 	       2 	   112
      25 	       2 	   110
      26 	       2 	   109
      27 	       2 	   107
      28 	       2 	   105
      29 	       2 	   104
      30 	       1 	   102
      31 	       1 	   101
      32 	       1 	   100
      33 	       1 	    99
      34 	       1 	    97
      35 	       1 	    96
      36 	       1 	    95
      38 	       2 	    93
      40 	       2 	    92
      42 	       2 	    90
      44 	       2 	    88
      46 	       1 	    87
      48 	       1 	    86
      50 	       1 	    84
      52 	       1 	    83
      54 	       1 	    82
      56 	       1 	    81
      59 	       1 	    80
      62 	       1 	    78
      65 	       1 	    77
      68 	       1 	    76
      71 	       1 	    75
      74 	       1 	    74
      78 	       1 	    73
      82 	       1 	    71
      86 	       1 	    70
      90 	       1 	    69
      95 	       1 	    68
     100 	       1 	    67
     105 	       1 	    66
     111 	       1 	    65
     117 	       1 	    64
     124 	       1 	    63
     131 	       1 	    62
     139 	       1 	    60
     147 	       1 	    59
     156 	       1 	    58
     166 	       1 	    57
     177 	       1 	    56
     189 	       1 	    55
     202 	       1 	    54
     216 	       1 	    53
     231 	       1 	    52
     247 	       1 	    51
     265 	       1 	    50
     285 	       1 	    49
     307 	       1 	    48
     331 	       1 	    47
     358 	       1 	    46
     388 	       1 	    45
     421 	       1 	    44
     458 	       1 	    43
     499 	       1 	    42
     545 	       1 	    41
     597 	       1 	    40
     655 	       1 	    39
     721 	       1 	    38
     796 	       1 	    37
     881 	       1 	    36
     978 	       1 	    35
    1090 	       1 	    34
    1219 	       1 	    33
    1368 	       1 	    32
    1542 	       1 	    31
    1746 	       1 	    30
    1986 	       1 	    29
    2270 	       1 	    28
    2608 	       1 	    27
    3013 	       1 	    26
    3502 	       1 	    25
    4098 	       1 	    24
    4830 	       1 	    23
    5737 	       1 	    22
    6873 	       1 	    21
    8312 	       1 	    20
   10157 	       1 	    19
   12555 	       1 	    18
   15719 	       1 	    17
   19967 	       1 	    16
   25780 	       1 	    15
   33911 	       1 	    14
   45574 	       1 	    13
   62798 	       1 	    12
   89119 	       1 	    11
  131011 	       1 	    10
  201051 	       1 	     9
  325498 	       1 	     8
  564342 	       1 	     7
 1071481 	       1 	     6
 2308074 	       1 	     5
 5996970 	       1 	     4
21202243 	       1 	     3
136998728 	       1 	     2

可以觀察到，從畫素 12 移動到 alfa 附近的畫素 11 需要 27 000 次迭代。計算到 alfa 附近 1 畫素內的點需要：2m1.236 秒

使用柯蒂斯·麥克穆倫的逆博特切爾對映繪製動態外部射線

使用麥克穆倫方法繪製帶有外部射線的茱莉亞集合

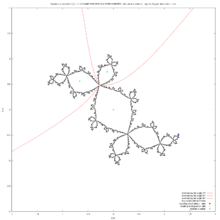
該方法基於柯蒂斯·麥克穆倫的 C 程式 及馬特亞茲·艾拉特的 Pascal 版本

這裡有兩個平面 

• w-平面（或 f0 平面）
• z-平面（fc 平面的動力學平面）

該方法包含 3 個主要步驟 

• 計算圓形外部射線在角 $\theta \,$ 和不同半徑（光柵化）上的某些 w 點

$w_{0}=R*e^{2\pi it}\,$ 其中 $1<R<\infty \,$

• 使用逆博特切爾對映將 w 點對映到 z 點 $\Psi _{c}=\Phi _{c}^{-1}\,$

$z_{0}=\Psi _{c}(w_{0})=f_{c}^{-n}(w_{0}^{2^{n}})\,$

• 繪製 z 點（並使用線段連線它們（線段是直線的一部分，由兩個不同的端點界定））

第一步和最後一步很容易，但第二步不容易，需要更多解釋。

光柵化

對於給定的外部射線，在 $f_{0}\,$ 平面 中，射線的每個點都有 

• 常數 $t\,$ （外角以轉為單位）
• 變數半徑 $R\,$

所以 $w\,$ 射線的點由半徑 $R\,$ 引數化，可以使用 複數的指數形式 計算。

$w=F_{t}(R)=R*e^{2*\Pi *i*t}\,$

可以使用 **線性尺度** 沿著射線前進。

t:1/3; /* example value */
R_Max:4;
R_Min:1.1;
for R:R_Max step -0.5 thru R_Min do w:R*exp(2*%pi*%i*t);
/* Maxima allows non-integer values in for statement */

這會得到一些 w 點，這些點之間的距離相等。

另一種方法是使用 **非線性尺度**。

為了做到這一點，我們引入浮點 指數 $r\,$，使得

$R=2^{r}\,$

和

$w=G_{t}(r)=2^{r}*e^{2*\Pi *i*t}\,$

為了計算外射線在 $f_{0}\,$ 平面上的角度為 $t\,$ 的一些 w 點，使用以下 Maxima 程式碼

t:1/3; /* external angle in turns */
/* range for computing  R ; as r tends to 0 R tends to 1 */
rMax:2; /* so Rmax=2^2=4 /
rMin:0.1; /* rMin > 0   */
caution:0.93; /* positive number < 1 ; r:r*caution  gives smaller r */
r:rMax;
unless r<rMin do
( 
 r:r*caution, /* new smaller r */ 
 R:2^r, /* new smaller R */
 w:R*exp(2*%pi*%i*t) /* new point w in f0 plane */
);

在這個方法中，點之間的距離並不相等，而是與填充的 Julia 集邊界距離 成反比。

這是好的，因為在這裡射線具有更大的 曲率，因此曲線會更加平滑。

對映

從 $f_{0}\,$-平面 到 $f_{c}\,$-平面 的對映包括 4 個小步驟

• 在 $f_{0}\,$ 平面中進行向前迭代

$w_{n}=w_{0}^{2^{n}}=R^{2^{n}}*e^{2\pi i2^{n}t}\,$

直到 $w_{n}\,$ 接近無窮大

$abs(w_{n})>R_{limit}\,$

• 切換平面（從 $f_{0}\,$ 到 $f_{c}\,$)

$z_{n}=w_{n}\,$

（因為這裡，接近無窮大：$w=z\,$）

• 在 $f_{c}\,$ 平面上進行反向迭代相同（$n\,$）次迭代次數
• 最後一個點 $z_{0}\,$ 在我們的外部射線上

步驟 1、2 和 4 很容易。第三個不容易。

$z_{n-1}=f_{c}^{-1}(z_{n})={\sqrt {z_{n}-c}}\,$

反向迭代使用複數的平方根。它是一個雙值函式，因此反向迭代會產生二叉樹。

在沒有額外資訊的情況下，無法在這樣的樹中選擇正確的路徑。為了解決這個問題，我們將使用兩件事

• 無窮大吸引域的等度連續性
• $f_{0}\,$ 和 $f_{c}\,$ 平面之間的共軛關係

無窮大吸引域的等度連續性

無窮大吸引域（填充的 Julia 集的補集）包含在正向迭代下趨於無窮大的所有點。

$A_{f_{c}}(\infty )\ {\overset {\underset {\mathrm {def} }{}}{=}}\ \{z\in \mathbb {C} :f_{c}^{(k)}(z)\to \infty \ as\ k\to \infty \}.$

無窮大是一個超吸引不動點，所有點的軌道都具有類似的行為。換句話說，如果兩個點的初始位置很接近，則它們的軌道被認為會保持接近。

這就是等度連續性（與正規性比較）。

在 $f_{c}\,$ 平面上，可以使用射線先前點的正向軌道來計算下一個點的反向軌道。

演算法的詳細版本

• 計算射線的第一個點（從無窮大附近開始，朝 Julia 集移動）

$w=2^{r}*e^{2\Pi it}\,$ 其中 $r=r_{max}\,$

這裡可以輕鬆切換平面

$z=w\,$

這是射線的第一個 z 點。

• 計算射線的下一個 z 點
  • 計算射線的下一個 w 點，對於 $r=r*caution\,$
  • 計算兩個點的正向迭代：前一個 z 點和當前 w 點。儲存 z 軌跡和最後一個 w 點
  • 切換平面並使用最後一個 w 點作為起點：$z_{n}=w_{last}\,$
  • 使用前一個 z 點的正向軌跡，對新的 $z_{n}\,$ 進行反向迭代，直到新的 $z_{0}\,$
  • $z_{0}\,$ 是射線的下一個 z 點
• 依此類推（下一個點），直到 $r<r_{Min}\,$

Maxima CAS 原始碼

/* gives a list of z-points of external ray for angle t in turns and coefficient c */
GiveRay(t,c):=
block(
 [r],
 /* range for drawing  R=2^r ; as r tends to 0 R tends to 1 */
 rMin:1E-20, /* 1E-4;  rMin > 0  ; if rMin=0 then program has infinity loop !!!!! */
 rMax:2,  
 caution:0.9330329915368074, /* r:r*caution ; it gives smaller r */
 /* upper limit for iteration */
 R_max:300,
 /* */
 zz:[], /* array for z points of ray in fc plane */
 /*  some w-points of external ray in f0 plane  */
 r:rMax,
 while 2^r<R_max do r:2*r, /* find point w on ray near infinity (R>=R_max) in f0 plane */
 R:2^r,
 w:rectform(ev(R*exp(2*%pi*%i*t))),
 z:w, /* near infinity z=w */
 zz:cons(z,zz), 
 unless r<rMin do
 ( /* new smaller R */
  r:r*caution,  
  R:2^r,
  /* */
  w:rectform(ev(R*exp(2*%pi*%i*t))),
  /* */
  last_z:z,
  z:Psi_n(r,t,last_z,R_max), /* z=Psi_n(w) */
  zz:cons(z,zz)
 ),
 return(zz)
)$

另請參見

• 引數外部射線
• 外部射線精度 - 重要性

參考文獻

• 外部射線的豪斯多夫極限：拓撲影像，作者：Carsten Lunde Petersen 和 Saeed Zakeri