現代物理學/時空中的波

狹義相對論
1 - 2 - 3 - 4 - 5 - 6

---

狹義相對論的應用

在本章中，我們將繼續研究狹義相對論，並將前一章中發展起來的思想應用於波的研究。

首先，我們將展示如何在時空的背景下描述波。然後我們看到，那些沒有優先參考系（例如支援它們的介質的參考系）的波，由於狹義相對論的約束，必須具有特定形式的色散關係。這種色散關係恰好是量子力學中相對論物質波的色散關係。

其次，我們將研究多普勒效應，其中波的頻率在不同的座標系中具有不同的值。

第三，我們將展示如何在相對論一致的情況下新增速度。這在討論狹義相對論中的粒子行為時也會很有用。

在相對論波的背景下，將介紹一個新的數學概念，即時空向量或四向量。用相對論標量和四向量完全寫出物理定律，可以確保它們在所有慣性參考系中都適用。

時空中的波

時空中的波

現在我們看看時空中的波的特徵。回想一下，一維空間中的波可以用以下公式表示

$A(x,t)=A_{0}\sin(kx-\omega t)\,$

其中 $A_{0}$ 是波的（常數）振幅，$k$ 是波數，$\omega$ 是角頻率，以及 $\phi =kx-\omega t$ 被稱為波的相位。對於三維空間中的波，波的表示方式類似，

$A(\mathbf {x} ,t)=A_{0}\sin(\mathbf {k} \cdot \mathbf {x} -\omega t)$

其中 $\mathbf {x}$ 現在是位置向量，$\mathbf {k}$ 是波向量。波向量的模，$|\mathbf {k} |=k$ 僅僅是波的波數，而該向量的方向指示著波的傳播方向。在這種情況下，波的相位是 $\phi =\mathbf {k} \cdot \mathbf {x} -\omega t$.

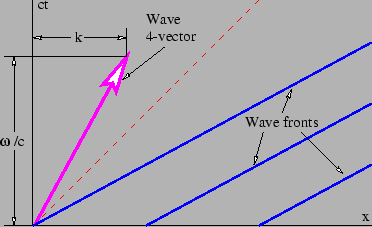圖 5.1：時空波前示意圖。大箭頭是相應的波四向量，其斜率為 $\omega /ck$。波前的斜率是其倒數，$ck/\omega$。

在一維情況下，$\phi =kx-\omega t$。波前具有恆定的相位$\phi$，因此求解該方程以獲得$t$，並乘以真空中的光速$c$，會得到波前世界線的方程。

$ct={\frac {ckx}{\omega }}-{\frac {c\phi }{\omega }}={\frac {ck}{u_{p}}}-{\frac {c\phi }{\omega }}\quad {\mbox{(波前).}}$

時空圖中世界線的斜率是$x$的係數，即$c/u_{p}$，其中$u_{p}=\omega /k$是相速度。