SA NC開展調查/第7章
| 開展調查:GET 和 FET 數學與科學教育工作者的資源手冊 |
這份資源手冊並非旨在成為一本關於調查的教科書,其中包含大量供教師參考的思路。任何給出的例子都旨在說明,即使是最常見的課堂活動,也可以以調查的方式進行。這裡提供的材料摘自2003年MSTotY獲獎者的作品集,清楚地證明了這一點。第一個活動是針對中間階段學習者的“分數”調查。因為它使用測量來解決主題,所以它適用於科學和數學。第二和第三個活動在FET物理學中很常見(牛頓第二定律和電磁電動機規則)。讀者會認識到,即使是熟悉的活動,透過稍微重新塑造它們,也可以符合“調查方法”的要求。我們可能會認為“調查”意味著學習者獨自工作並研究吸引他們想象力的私人話題。但這並非總是如此,具有特定焦點和教育工作者指導的活動也可以是調查。
在三個示例中的第一個示例中,學習者會得到一系列遵循分數邏輯的活動,並且學習者透過測量來學習這些活動。事實上,測量本身是調查的一個重要方面。因此,我們現在有了“調查方法”的教學和學習,而不是討論學習者“對私人主題的自由調查”,即純形式。學習者的自由調查是調查方法的一個特殊子集。重要的是,無論學習者遵循自己的好奇心還是由教育工作者引導他們遵循邏輯順序,在兩種情況下,他們都在以一種遵循數學和科學邏輯和本質的方式進行調查。教育工作者主導的調查的優勢在於,即使在“現實世界”中可能沒有那麼整潔和有順序,也可以向學習者展示一種邏輯方法(例如,在進入下一階段之前提出並回答一個關鍵問題)。透過獲得這種指導經驗,學習者應該在他們的自由調查中採用類似的方法。第一次調查是由Vanessa Thayer進行的,她是2003年年度數學和科學教育工作者獎的獲得者。Vanessa 承認該活動的最初靈感和部分內容的來源。對於專業人士來說,這樣做很重要,因為他們必須高於剽竊和其他人的想法未經認可的使用。使用分米研究分數:對分數和測量的調查
特別說明 本模組中的所有活動均改編自西開普省教育廳(WCED)開普敦教學研究所為中間階段數學教育工作者舉辦的職前培訓課程中收到的教學材料和思路。
早在4000多年前,甚至在金字塔建成之前,古埃及人就已經提到了分數。測量被用來測量農場。他們最初使用他們的肘部和手指,但這效果不佳,因為不同人的肘部和手指長度不同。
在追求準確性的過程中,他們使用標準單位作為較大單位的等份,例如分米尺。然而,他們現在發現他們有一整袋尺子,這也很不方便。因此,他們後來使用十分之一、百分之一、千分之一(小數),但必須堅持使用普通分數(一半和四分之一),例如,不能用小數測量一米。 (讓學習者回到過去,使情境變得真實。)
我們教授分數是為了為小數分數提供基礎。我們特意在測量的背景下研究普通分數,以便讓學習者有機會發現分數開始的背景,最重要的是,瞭解等價、簡單、帶分數等的邏輯以及普通分數和小數之間的關係。透過這種方式,學習者能夠制定自己的規則/方法,並且在更高的年級也會理解規則、方法和公式背後的邏輯。
活動模組為學習者提供了許多機會來討論他們所做的事情並與其他學習者互動,這是一種讓學習者意識到他們如何學習、建立他們的溝通能力,最重要的是,參與邏輯的有效方法。
儘量不要急於使用尺子的具體支援。透過這種方式,學習者將內化邏輯,並且以後能夠自信地處理抽象情境。確保學習者使用正確的分數語言。鼓勵他們說,例如,四分之三,而不是四分之三。在下一個活動模組中,學習者將有機會在許多其他不同的情境中使用分數。
評估計劃 學習領域:數學,RNCS 五年級學習結果:L 01:數、運算和關係 L 04:測量
- 識別並表示不同分母的常見分數,包括二分之一、三分之一、四分之一、五分之一、六分之一、七分之一、八分之一,以便描述和比較它們。
- 識別並使用分母互為倍數的常見分數的等值形式,以及在測量情境中使用形式為 0.5、2.5 等的小數。
- 識別並表示至少到十二分之一的常見分數,以便描述和比較它們。
- 識別並使用分母互為倍數的常見分數的等值形式,以及在測量情境中使用形式為 0.5、2.5 等的小數。
- 識別並表示常見分數,包括十分之一、百分之一和百分比。
- 識別並使用分母為一位數或兩位數的常見分數的等值形式。
- 至少到小數點後兩位的小數。
- 百分比。
- 識別、分類和表示小數(至少到小數點後三位)、分數和百分比。
- 識別並使用有理數的等值形式,包括常見分數、小數、百分比。
預期成果:學習者能夠用分數表示法展示對“一小時”的理解。方法:筆試 技巧:練習冊 評估工具:評估表格
預期成果:學習者能夠識別、表示、描述、比較並在測量情境中將常見分數轉換為等值形式。方法:筆試 技巧:練習冊 評估工具:以下評分標準,使用四個成就水平描述符。
[LO1:數、運算和關係 L 04:測量] 年級評估標準:學習者能夠識別、表示、描述、比較並在測量情境中將常見分數轉換為等值形式。
|
使用分米研究分數的評分標準。 | ||||
|---|---|---|---|---|
|
評估標準 |
4 優秀成就 |
3 達到要求標準 |
2 部分達到標準 |
2 部分達到標準 |
|
A. 表示常見分數 |
非常注重測量的準確性和細節。 |
正確繪製了深色和淺色紙片,給出了每張紙片的分數測量值。 |
至少有一張紙片被正確表示。 |
沒有一張紙片被正確表示。 |
|
B. 識別常見分數 |
識別了淺色和深色紙片的厚度,沒有錯誤。 |
使用大多數尺子識別了淺色和深色紙片的厚度。 |
使用一些尺子識別了淺色和深色紙片的厚度。 |
沒有證據表明正確使用了尺子來識別分數。 |
|
C. 在分數的等值形式之間轉換 |
預測用於測量樣品紙片 A-E 的所有等值尺子都是正確的。 |
預測用於測量樣品紙片 A-E 的大多數等值尺子都是正確的。 |
預測用於測量樣品紙片 A-E 的一些等值尺子是正確的。 |
幾乎沒有預測用於測量樣品紙片 A-E 的等值尺子是正確的。 |
|
D. 比較分數 |
所有分數單位都從最小到最大準確排列。 |
大多數分數單位的尺子都從最小到最大準確排列。 |
有證據表明學習者可以將尺子從最小到最大排列,但有一定的困難。 |
沒有一個尺子從最小到最大準確排列。 |
|
E. 描述常見分數(使用正確的分數表示法) |
所有分數都用正確的分數表示法描述(在測量情境中)。 |
大多數分數都用正確的分數表示法描述(在測量情境中)。 |
一些分數用正確的分數表示法描述,但沒有測量情境。 |
沒有證據表明理解了分數表示法。 |
報告程式碼:評論
________________________________________________________________________________
________________________________________________________________________________
|
簽名:家長/監護人 |
日期 |
教育工作者簽名 |
把你的普通尺子收起來。你只需要使用這裡提供的特殊尺子。
你將使用分米作為單位。在這裡你可以看到大約一分米有多長。
|
|
1. 剪下一條與上面“練習分米”一樣長的紙條。現在你為自己製作了一個“一分米尺”。
2. 用你的練習尺檢查下面的鉛筆是否正好 2 分米長。如果不是,它是大於還是小於還是大約(近似)2 分米長?
3. 用你的練習分米測量下面大理石板的長度和寬度。它是一個正方形嗎?
4. 用你的練習分米測量你的桌面邊緣。
5. 用練習分米尺準確測量你的桌面是否可能?與朋友討論一下。
[如果複製,請使用接下來的兩頁作為影印母版或示例。確保尺子 ABCD、EFGH 和 JKMN 在影印後都正好為 20 釐米。頁面可能需要稍微放大。如果重新繪製,請確保任何一個尺子的細分都完全相等。例如,尺子 D 中的所有小細分都必須正好為 1 釐米長。]
[關鍵:E(30 分之一),F(15 分之一),G(24 分之一),H(16 分之一),J(20 分之一),K(25 分之一),M(40 分之一),N(50 分之一)]
剪下尺子(上面有尺子 A、B、C 和 D),沿著虛線摺疊。這樣你就可以製作自己的分米尺組。
1. 量尺B的下半部分每個小格的長度是多少?寫下你的答案。
2. 量尺C的下半部分每個小格的長度是多少?寫下你的答案。
3. 量尺D的下半部分每個小格的長度是多少?寫下你的答案。
西姆菲韋測量了下一頁的每支鉛筆。以下是他的測量結果
- 鉛筆A的長度略小於1.5分米。
- 鉛筆B的長度大約在1.5分米和2分米之間。
- 鉛筆C的長度正好是2分米。
- 鉛筆D的長度略小於2分米。
- 鉛筆E的長度正好是1.5分米。
- 鉛筆F的長度正好在1.5分米和2分米之間。
- 鉛筆G的長度略大於2分米。
4. 使用你新的分米尺檢查西姆菲韋的每個測量結果。完成測量後,與你的小組成員比較你的發現。
馬羅塔先生試圖測量這條蚯蚓。
首先,他嘗試用十分之一分米尺測量它。
你能看到十分之一分米尺不適合測量這條蚯蚓嗎?你只能說這條蚯蚓的長度略大於0.6分米,並且小於0.7分米。
然後,馬羅塔先生嘗試用十二分之一分米尺。
接下來,他嘗試用八分之一分米尺。
馬羅塔先生現在非常高興。他成功地相當精確地測量了這條蚯蚓。他寫道:這條蚯蚓長5/8分米。
1. 下面的蚯蚓有多長?
2. 測量下面每支鉛筆的長度。對於每支鉛筆,你必須找到完全匹配的量尺。在每種情況下,像馬塔先生那樣寫下你的答案。
1. 使用你的新量尺精確測量鉛筆B、E和F的長度。
2. 與你的小組成員比較你的結果。
3. 再次獨自完成。使用你的其中一把量尺畫一條正好0.7分米長的線段。
4. 使用你的其中一把量尺畫一條正好5/16分米長的線段。
5. 向你的小組成員解釋你是如何完成問題4的。
6. 使用你的其中一把量尺畫一條正好17/20分米長的線段。
等值分數
更小的部分
西姆菲韋想要研究魚在食用不同種類食物時是如何生長的。所以他想要精確地測量這條小魚的長度。
西姆菲韋嘗試了他所有的不同分米尺。
1. 西姆菲韋現在能準確地說出魚的長度嗎?
2. 本說這條魚長9/12分米。你同意嗎?
3. 製作兩把新的分米尺,一把透過剪下和摺疊量尺EFGH製作,另一把透過剪下和摺疊量尺JKMN製作。4. 對於每把新量尺,計算分米的小細分,並在量尺上寫下它們是分米的幾分之幾,例如量尺E(30分之一)。
4. 使用量尺EFGH精確測量上面魚的長度。寫下你的答案。
分數的語言(等值分數)
使用量尺EFGH和JKMN精確測量這些魚的長度。寫下你最好的答案,例如:魚X長19/24分米。
與你的小組成員比較你的結果。
等值分數:相同長度的不同描述
解決分歧
茨瓦內洛和西姆菲韋對於魚D、F和G的長度存在分歧。以下是茨瓦內洛的測量結果
- 魚D長3/4分米。
- 魚F長8/10分米。
- 魚G長21/24分米。
以下是西姆菲韋的測量結果
- 魚D長15/20分米。
- 魚F長16/20分米。
- 魚G長7/8分米。
獨立完成。1. 使用你所有的分米尺,調查魚D、F和G的長度情況。
2. 寫一封信給茨瓦內洛和西姆菲韋,幫助他們解決他們的分歧。(小組合作)
這是茨瓦內洛測量魚D的方式。
茨瓦內洛發現他可以用兩種方式描述魚D的長度。他可以說它長3/4分米。
他也可以說它長6/8分米。
3. 是否也可以用其他量尺測量魚D?
西姆菲韋發現魚D也可以用十二分之一分米更精確地測量。寫下魚的長度,用十二分之一分米表示。
4. 武約說:魚D長4又12/6分米。他說的對嗎?
5. 書面解釋為什麼3/4分米和9/12分米實際上是相同的長度。與你的小組成員比較你的解釋。
6. 再次獨立完成。書面解釋為什麼4又12/6分米和9/12分米實際上是相同的長度。在小組內比較你們的解釋。
等值分數問題
1. 使用你的量尺檢查15/20分米是否與9/12分米相同長度?寫下你答案的理由。
2. 與你的小組成員比較你對問題6的回答。
3. 如果魚C長23/30分米,你認為它可以用六十分之一分米更精確地測量嗎?首先自己思考並得出結論,暫時不要與你的小組成員討論。
4. 某條魚X的長度正好是3/5分米。寫下你可以用來精確描述魚X長度的所有其他方法。
5. 與你的小組成員比較你的答案。
6. 另一條魚,魚Y的長度正好是10/16分米。寫下你可以用來精確描述魚Y長度的所有其他方法。
7. 與你的小組成員比較你的答案。
組合部分
房屋有時使用水泥板而不是磚塊建造。工廠生產的水泥板厚度並不完全相同。由於不同厚度的板材用於不同的用途並以不同的價格出售,因此有時需要非常仔細地測量板材。
下面的水泥板樣品厚度為3/24分米(24分之3分米),如你所見。

測量以下每個水泥板樣品的厚度。使用你剪出的分米尺,並努力進行非常精確的測量。

與你的小組成員比較你的答案。你必須達成一致。
有時將兩張或多張板材連線在一起以製作一張更厚的板材。你可以在下面看到一個例子。這些組合的板材稱為複合板。測量下面複合板的深色和淺色部分的厚度。進行儘可能精確的測量。

1. 使用二十分之一分米尺(量尺J),
- 測量較深的板材
- 測量結果 _____________ 分米。
- 測量較淺的板材
- 測量結果 _____________ 分米
- 測量複合板
- 測量結果 _____________ 分米
2. 使用二十四分之一分米尺(量尺G),
- 測量較深的板材
- 測量結果 _____________ 分米。
- 測量較淺的板材
- 測量結果 _____________ 分米
- 測量複合板
- 測量結果 _____________ 分米
3. 非常精確地繪製你自己的複合板,如下所示
- 複合板的總厚度必須是 分米。(使用量尺A)
- 較深的板材必須是 分米。(將其塗黑。)
4. 使用量尺A、E、D、F給出數字3中較深、較淺和複合板的厚度測量結果。
|
分米尺 |
較淺的板材 |
較深的板材 |
|
A |
| |
|
E |
| |
|
D |
| |
|
F |
|
5. 檢查你所有淺色板材的測量結果,並將其與深色板材的測量結果進行比較。你是否看到了某種規律?寫下你的觀察結果。
6. 小組合作。討論如何利用這種規律,在不使用量尺A、E、D和F的情況下,獲得你的複合板的量尺A、E、D和F的測量結果。
7. 你討論中最重要的結論是什麼?寫下來。____________________________________________________________________________________________________________________________________ ____________________________________________________________________________________________________________________________________ ____________________________________________________________________________________________________________________________________
利用等值分數的邏輯來找到一種找出規律的方法。
黛安測量了一些複合板的樣品並記錄了她的結果。這些結果在下表中給出。對於每次測量,請說明還可以使用哪些其他尺子精確測量該板。在各列中寫下該尺子的精確測量值。(透過比較尺子檢查你的答案。將它們並排放置以進行此操作。)
複製此表並填寫你的答案。
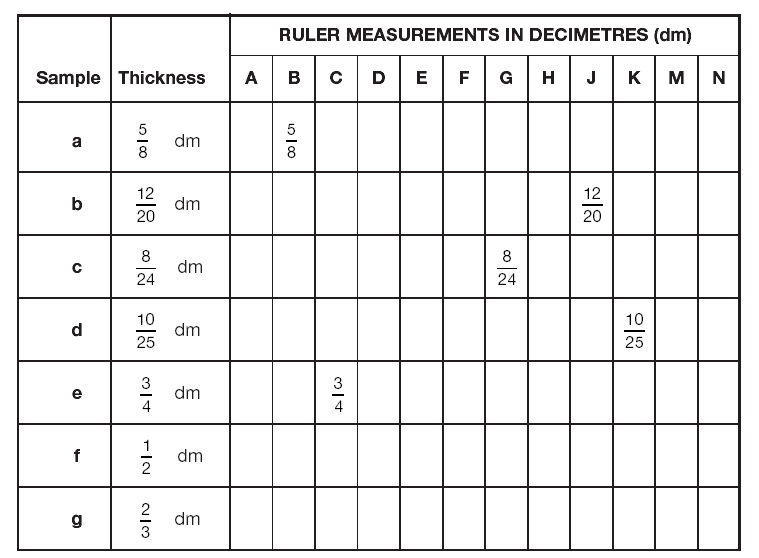
3. 將你尺子上的所有分數單位從大到小列出。____________________________________________________________________________ ____________________________________________________________________________
4. 當你寫下這個序列時,你的腦海中想到了什麼?____________________________________________________________________________ _____________________________________________________________________________
十分之一和百分之一。
這是一把非常精細的分米尺。

它實際上是一把十分之一尺,但分米的十分之一又被分成 10 個更小的單位。
1. 上述尺子上共有多少個小單位?
2. 使用你的一把“舊”分米分數尺(ABCD、EFGH 或 JKMN)測量下一頁所有板樣品的厚度。
3. 現在用你的新(百分之一)尺測量板樣品。
4. 以兩種方式計算以下每種複合板的厚度,首先透過將你在分米其他分數部分的測量值相加,然後透過將你在分米百分之一部分的測量值相加。
|
|
其他分數 |
其他分數 |
|---|---|---|
|
A + C |
|
|
|
B + D |
|
|
|
A + D + E |
|
|
|
B + F |
|
|
|
A + E + F |
|
|
使用十分之一和百分之一尺

小組工作:只有在你完成任務後才能討論此任務。
1. 圈出使測量板厚度更容易的尺子 a. 我們的舊 dm 尺 b. 十分之一和百分之一尺
2. 當我們使用十分之一和百分之一尺進行測量時,我們稱這種分數為
- ____________________________.
3. 使用你的舊 dm 尺和你的十分之一和百分之一尺測量板 A(上圖)。用數字和文字寫下測量值。
- _______________________________________________________________________
- _______________________________________________________________________
- _______________________________________________________________________
4. 你認為為什麼發明了十分之一和百分之一尺?
- _______________________________________________________________________
- _______________________________________________________________________
- _______________________________________________________________________
- _______________________________________________________________________
5. 十分之一和百分之一尺是否與舊的 dm 尺執行相同的工作?
- ______________
6. 它們之間有什麼區別?有什麼不同?
- _______________________________________________________________________
- _______________________________________________________________________
- _______________________________________________________________________
使用小數記法寫分數 - 寫分數的不同方法
我們可以用 0,7 代替寫 7/10。“0,7”讀作“零點七”,或簡稱為“點七”。
我們可以用 0,07 代替寫 7/100。這讀作“零點零七”,或簡稱為“點零七”。
我們可以用 2,37 代替寫 2 37/100。這讀作“二點三七”。
這種寫十分之一和百分之一的方法稱為小數記法。
1. 將以下每個長度用小數記法表示,然後求出這些長度的和:a. 3 dm + 1/10 dm + 4/100 dm b. 1 dm + 7/10 dm + 4/100 dm c. 3 dm + 5/10 dm + 9/100 dm d. 3 dm + 5/10 dm e. 3 dm + 5/100 dm
2. 與合作伙伴或小組一起檢查你的答案,並比較你使用的方法。
3. 使用你的十分之一/百分之一測量值將板 A-F 從最厚到最薄排列。
4. 使用小數記法寫下它們的分米厚度。
5. 計算你可以用任何兩塊板製成的最厚的複合板,並用分米和小數記法寫下厚度。
6. 計算你可以用任何兩塊板製成的最薄的複合板,並用分米和小數記法寫下厚度。
a. 輸入“.2 + .05 =”並寫下答案
- __________
b. 將 (a) 的答案寫成普通分數
- __________
c. 25 個百分之一也等於分米的 ____ 部分。(1 1/10、4/12、3/4、1/2、1/4)
d. 進行以下計算,並像上面 (a)、(b) 和 (c) 中一樣寫出來
- .7 + .05 = ___
- .3 + .45 = ___
- .12 + .13 = ___
- .2 + .55 = ___
- .38 + .12 = ___
接下來的活動涵蓋了 FET 物理中的兩個重要主題。它們以非常傳統的形式呈現,但與分數的中間階段研究一樣,這些活動可以以探究的方式進行教學。不同之處在於,如果教育者的控制力很強,那麼活動將不那麼具有探究性。如果它不那麼以教育者為中心,即他/她給予學習者更多對活動的控制權,那麼它將更具探究性。我們必須再次指出,探究的精神主要在於個別教育者在教學和學習中採用的方法。
在課程結束時,學習者應該能夠
- 繪製力和加速度的關係圖並進行解釋。
- 說明物體的加速度與產生該加速度的力之間的關係。
- 將這種關係應用到他們的日常生活經驗中
實驗/探究
記時打點計時器、記時紙帶、米尺、跑道、支撐跑道的書籍、細繩、滑輪、一些 10 克的砝碼、座標紙、工作紙、鉛筆、橡皮擦、尺子、科學計算器、粉筆、黑板擦。
大多數 12 年級教科書和實踐工作紙建議,在進行這項研究時,可以用橡皮筋或彈簧秤對小車施加兩倍或三倍的力。任何嘗試過這種方法的人都會發現,在保持一個或兩個橡皮筋長度不變的同時,隨著小車一起移動是非常困難的。透過使用砝碼(即“重量”,如所述)代替橡皮筋,可以避免這種困難。任何相同的物體,例如 10 克的砝碼都可以達到目的。
- 將一個砝碼系在細而結實的線上。
- 使用上油的滑輪。(見上圖。)
- 啟動記時打點計時器,然後釋放小車。防止它撞壞。
- 一次增加一個砝碼,並重復此過程,直到小車的加速度過高,無法獲得有用的結果。
- 需要克服的問題:記時打點計時器沒有留下清晰的標記,以及小車執行偏斜。
- 學習者必須掌握正在研究的概念以及實驗結果永遠不會“完美”的事實。
- 小車的跑道可以用舊門製作。
將學習者分成小組,每個小組最多四名學習者。
教育者在黑板上畫出這個圖……並問道:“如果兩個力同時作用在物體上,會發生什麼?”
- (預期答案:“物體將保持靜止,因為它上面沒有合力。”)
然後,教育者畫出另一個圖……並問道:“如果將這兩個力施加到物體上,會發生什麼?”
- (預期答案:“物體將向右移動,因為它上面有一個 2N 的合力。”)
教育者透過參考以前的知識鞏固答案:如果物體處於靜止狀態,它將保持靜止;如果物體在運動,它將永遠以恆定的速度沿直線運動,前提是物體上沒有合力。(NI)
然後,教育者在黑板上寫下研究的目的是什麼。

研究增加質量對加速度的影響

- 教育者分發準備好的工作紙,並描述實驗步驟(此時不提及“加速度”),包括如何根據記時打點計時器和紙帶確定物體的運動。
- 這裡提到,當資料充足時,可以將這些資料繪製成圖表。
- 學習者圍坐在桌子旁,觀察教育者製作第一條紙帶。
- 與班級達成共識,確定要使用的系列質量,並讓學習者自己製作其餘的紙帶。
- 商定查詢紙帶上每個點之間的時間間隔的方法,並計算T。
- 學習者現在分析每條紙帶。(丟棄紙帶上的前幾個點和後幾個點,使用中間部分。)
- 注意:如果打點計時器不可用,可以製作帶有可分析點的紙帶。雖然這樣做並非理想,但肯定比純粹將活動作為課本練習要好。
- 學習者計算每個時間間隔(即紙帶上點之間)的平均速度,並在工作紙上記錄這些速度。
- 在同一張圖表紙上,繪製每條紙帶的速度與時間的關係圖,並計算每條紙帶的“速度變化率”(即對於不同的質量)。
- 提出問題,引導學習者理解,透過改變繩子上的質量,他們改變了作用在小車上力的大小。
- 引入加速度的概念:速度的變化率。計算加速度的單位。
- 將一系列v-t圖的斜率表示為加速度。
- 提出問題:“是什麼導致了小車的加速度?”
- (預期答案:“透過改變砝碼的數量,改變作用在小車上的力。”)
建議繪製圖表來尋找力和加速度之間的關係。使用“砝碼數量”作為自變數(x軸),加速度作為因變數(y軸)繪製圖表。
- 是否存在直線關係?在加速度與合力圖上繪製“最佳擬合”線(即最接近大多數點的線)。
- 討論
- 圖上是否存在直線趨勢?(對該裝置進行精心執行的測試通常會導致直線趨勢。)
- 如果不是,什麼因素可能影響實驗過程?(摩擦會影響加速度的大小,但由於它是一個運動方向上的力,因此不會影響圖表的線性關係。這裡不必討論摩擦隨運動物體速度變化的事實,因為影響可能在實驗誤差範圍內。)
教育者與班級討論這些問題,並澄清加速度與合力之間直線圖的含義。(10分鐘)
- 結論
如果存在直線趨勢,則表明存線上性關係,可以表示為
- "a與1/F成正比"
- 解釋說,這被稱為牛頓第二運動定律,並向班級展示數學公式,包括質量(小車的質量,而不是砝碼的數量)作為常數(比例常數)。
要求學習者帶來關於加速度和力之間關係在其日常經驗/實際情況中明顯的書面資訊,例如,一個人和兩個人推動停滯汽車的區別以及產生的加速度。
關於電磁學的這個探究的妙處在於,它幾乎與19世紀初邁克爾·法拉第在英國和約瑟夫·亨利在美國進行的探究型別相同。他們的開創性工作導致了今天推動我們工業發展的偉大的電動機和發電機。
在課程結束時,學習者應該能夠
- 應用左手定則確定磁場中導體所受的力。
- 說明並理解影響此力的因素。
- 列舉此力的實際應用。
學習者探究
鐵架臺、U型磁鐵、銅導線(x2)、手電筒電池(x4)、電路板、為本實驗設計的銅片。
教育者將學習者分成3組——每組至少8名學習者。
教育者提出以下問題:“導線中的電流會產生什麼影響?描述你見過的任何影響。”
- (預期答案:加熱、照明、磁效應和化學效應。)
教育者從學習者已經瞭解的現象開始。此時不要解釋電流與其磁效應之間的關係。
教育者在黑板上寫下當天的主題。“探究磁場中載流導體上的力”。
探究磁場中載流導體所受的力。
教育者發放工作紙,解釋實驗裝置(見下圖),並讓學習者按照說明進行操作。
教育者討論觀察到的任何力的影響(即運動——參見NII),並引出學習者對影響觀察到的力的變數的觀察/意見,例如,增加磁場強度或增加磁場中導體的長度。總結在黑板上,並讓學習者記下補充資訊。
對於本次探究,使用建議的材料或類似的材料搭建此裝置。裝置並不複雜,可以使用廢料或低成本材料組裝。
注意:在廢棄冰箱的門上很容易找到磁鐵。舊電線和手電筒電池也可以找到或以非常便宜的價格購買。
獲取3根金屬線,最好是銅線,並將它們製成以下三種形狀。
按照圖示搭建實驗裝置。
當電流流過導線時,導線1必須能夠在與導線2和3連線的環形接頭上自由移動。
導線1必須能夠自由地進入或離開磁鐵,如虛線箭頭所示。知道U型磁鐵的哪一端是北極。
現在將電池的端子連線到導線2和3,以完成裝置。(在理想世界中,並且有無限的時間,人們會讓學習者提出問題——“找出……之間的關係等等”——並讓他們設計實驗裝置來測試這些關係並得出答案。不幸的是,很少有教育者能負擔得起這種奢侈,因此實驗裝置是“給定”的。)
1. 按照圖示搭建實驗裝置。
2. 閉合開關,觀察導體1的變化。
3. 導體向哪個方向移動?
- ....................................................................................................
4. 改變連線的極性,即正負極。現在導體1向哪個方向移動?
- ....................................................................................................
5. 改變接線柱的極性會影響導體的運動嗎?
- ....................................................................................................
6. 閉合開關。觀察並記錄發生的現象。
- ....................................................................................................
7. 反轉磁場的極性。這會影響導體的運動嗎?
- ....................................................................................................
8. 你的觀察結果(2 Â ­ 7)是否一致?你是否預料到觀察到的現象?請回答並解釋你的答案。
- ....................................................................................................
9. 繪製示意圖,展示磁場方向(慣例:北到南)、導體1中電流方向(慣例:從電池正極到負極)和導體1上力的方向之間的關係。
10. 在繪製完解釋性示意圖後(三個方向都相互垂直,即示意圖必須顯示三個維度:頁面上的上下、頁面上的左右以及頁面內外的方向)。
11. 完成示意圖後,回到實驗裝置,檢查示意圖的預測價值。介紹弗萊明左手定則,讓學習者檢查該定則與他們示意圖的一致性。
12. 增加電路中電池的數量,並記錄導體1的偏轉情況。與只使用一個電池時相比,偏轉幅度更大還是更小?
- ....................................................................................................
13. 即使電流強度增加,力的方向是否與你預測的一致?
- ....................................................................................................
14. 當電池數量增加時,導體所受的力是增大還是減小?
- ....................................................................................................
15. 鑑於增加電池數量也會增加電流(歐姆定律),從這個觀察結果可以得出什麼結論?
- ....................................................................................................
16. 繪製概念圖,並寫出關於磁場中載流導體的受力效應的總體結論。
- ....................................................................................................
